1 モーターサイクルの運動学

モーターサイクルの運動学的研究は、特にそのモーターサイクルの動的挙動に及ぼす影響に関連して重要です。したがって、この章では、運動学的研究に加えて、モーターサイクルの動的挙動のいくつかの簡単な例を報告し、運動学的特異点がモーターサイクルの方向安定性と操縦性にどのように影響するかを示します。

1.1 モーターサイクルの定義

モーターサイクルは、多種多様な機械部品で構成されていますが、いくつかは複雑なものも含まれます。しかし、厳密に運動学的な観点からは、サスペンションを剛体と見なすことで、モーターサイクルは単純に4つの剛体からなる空間メカニズムとして定義できます。

• リアアセンブリ（フレーム、サドル、タンク、モーター・トランスミッションドライブトレイングループ）
• フロントアセンブリ（フォーク、ステアリングヘッド、ハンドルバー）
• フロントホイール
• リアホイール

これらの剛体は、3つの回転ジョイント（ステアリング軸と2つのホイール軸）で接続され、図1-1に示すように、地面と2つの車輪/地面接触点で接地しています。 各回転ジョイントは、空間メカニズム内の5つの自由度を拘束し、各車輪-地面接触点は3つの自由度を残します。道路上のタイヤの純粋な転がりの仮説が有効であると考えると、各車輪は固定された道路に対して次のようにのみ回転できることが容易に確認できます。

• 車輪面上の接触点（前進運動）
• モーターサイクルと道路平面の交差軸（ロール運動）
• 接触点と車輪中心を結ぶ軸（スピン）

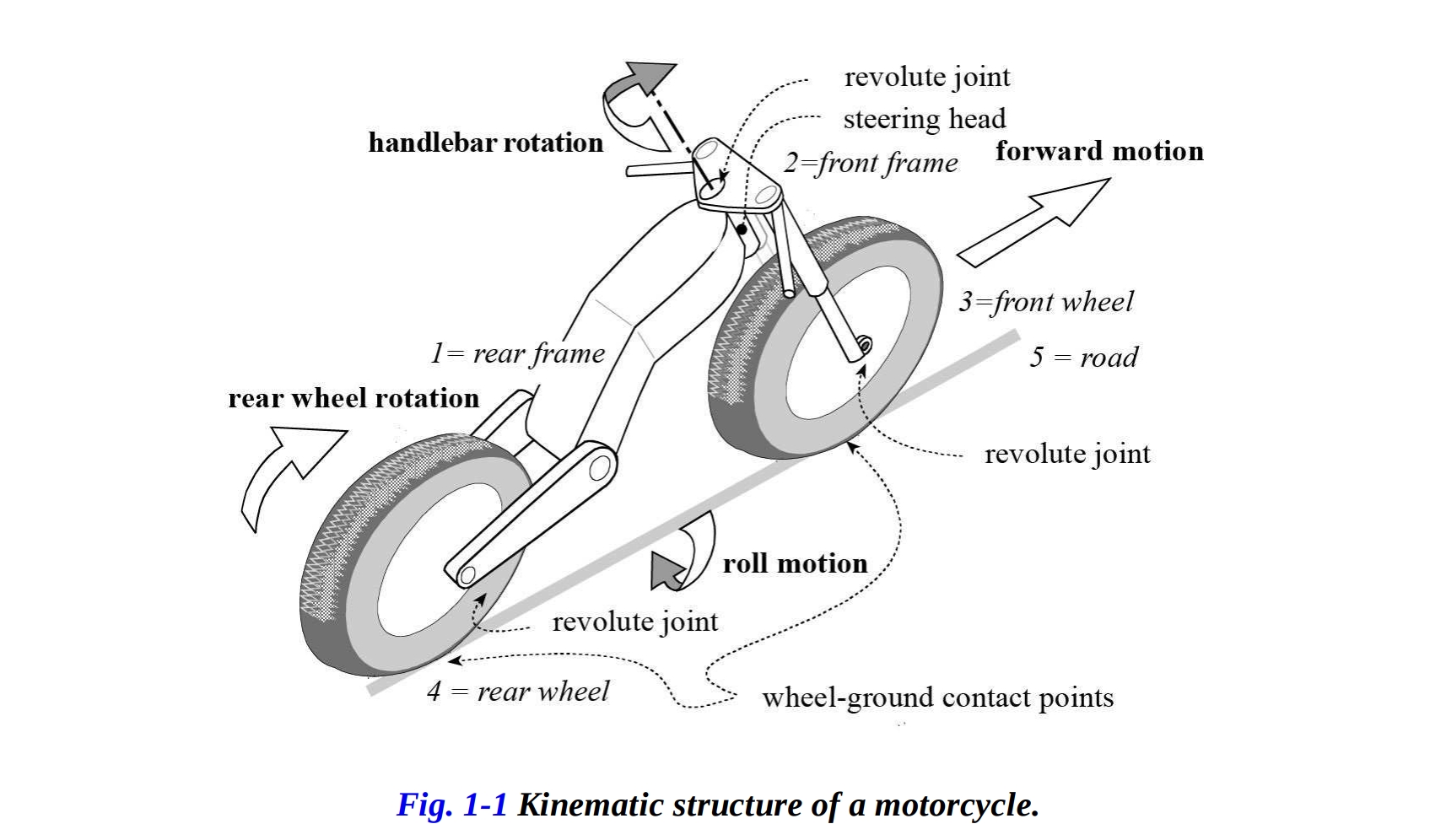
図1-1 モーターサイクルの運動学的構造。

つまり、モーターサイクルの自由度の数は、3であり、これは、3つの回転ジョイントによって拘束される15の自由度と、2つの車輪-地面接触点によって除去される6つの自由度が、4つの剛体の24の自由度から減算される必要があるためです（図1-2）。

モーターサイクルの3つの自由度は、次の3つの主要な運動に関連付けることができます。

• モーターサイクルの前進運動（リアホイールの回転によって発生する）
• 路面平面上のタイヤ接触点を結ぶ直線を中心とするロール運動
• ステアリングの回転

ライダーは運転中に、自身の個人的なスタイルと技能に応じて、これらの主要な3つの運動を操ることになります。モーターサイクルの結果と対応する軌跡（曲線）は、時間領域における3つの運動に関連する組み合わせに依存します。これにより、可能な数千の中から1つの操作が生成され、これがドライバーの個人的なスタイルが生まれます。

これらの考慮事項は、タイヤが滑りなしで移動すると仮定して定式化されています。ただし、現実には、タイヤの運動は単なる転がりプロセスだけではありません。縦方向力（駆動力およびブレーキング力）および横方向力の発生には、路面状況に応じて、縦方向および横方向のいくらかの滑りが必要です。したがって、自由度の数は7になります。

• モーターサイクルの前進運動
• ロール運動
• ハンドルバーの回転
• フロントホイールの縦方向の滑り（ブレーキング）
• リアホイールの縦方向の滑り（推進またはブレーキング）
• フロントホイールの横方向の滑り
• リアホイールの横方向の滑り

1.2 モーターサイクルの幾何学

この運動学的研究は、サスペンションのない剛性のモーターサイクル、つまり非変形タイヤに装着された車輪で構成され、円形断面を持つ二つのトロイダルな固体ボディとして模式化されています（図1-3）。

モーターサイクルは、以下の幾何学的パラメータを使用して記述できます：

• p: ホイールベース
• d: フォークオフセット（ステアリングヘッドの軸とフロントホイールの中心との垂直距離）
• ε: キャスター角
• Rr: リアホイールの半径
• Rf: フロントホイールの半径
• tr: リアタイヤの断面半径
• tf: フロントタイヤの断面半径

いくつかの重要な幾何学的パラメータは、これらの変数で表すことができます：

• ρr = (Rr - tr)：フロントトーラス中心円の半径
• ρf = (Rf - tf)：リアトーラス中心円の半径
• an = Rf sin ε - d：法線トレイル
• a = an / cos ε = Rf tan ε - d / cos ε：機械トレイル

モーターサイクルを記述するために通常使用される幾何学的パラメータは以下のとおりです：

• ホイールベースp
• キャスター角ε
• トレイルa

これらのパラメータは、モーターサイクルを垂直位置に置き、ハンドルバーのステアリング角度をゼロに設定した状態で測定されます。

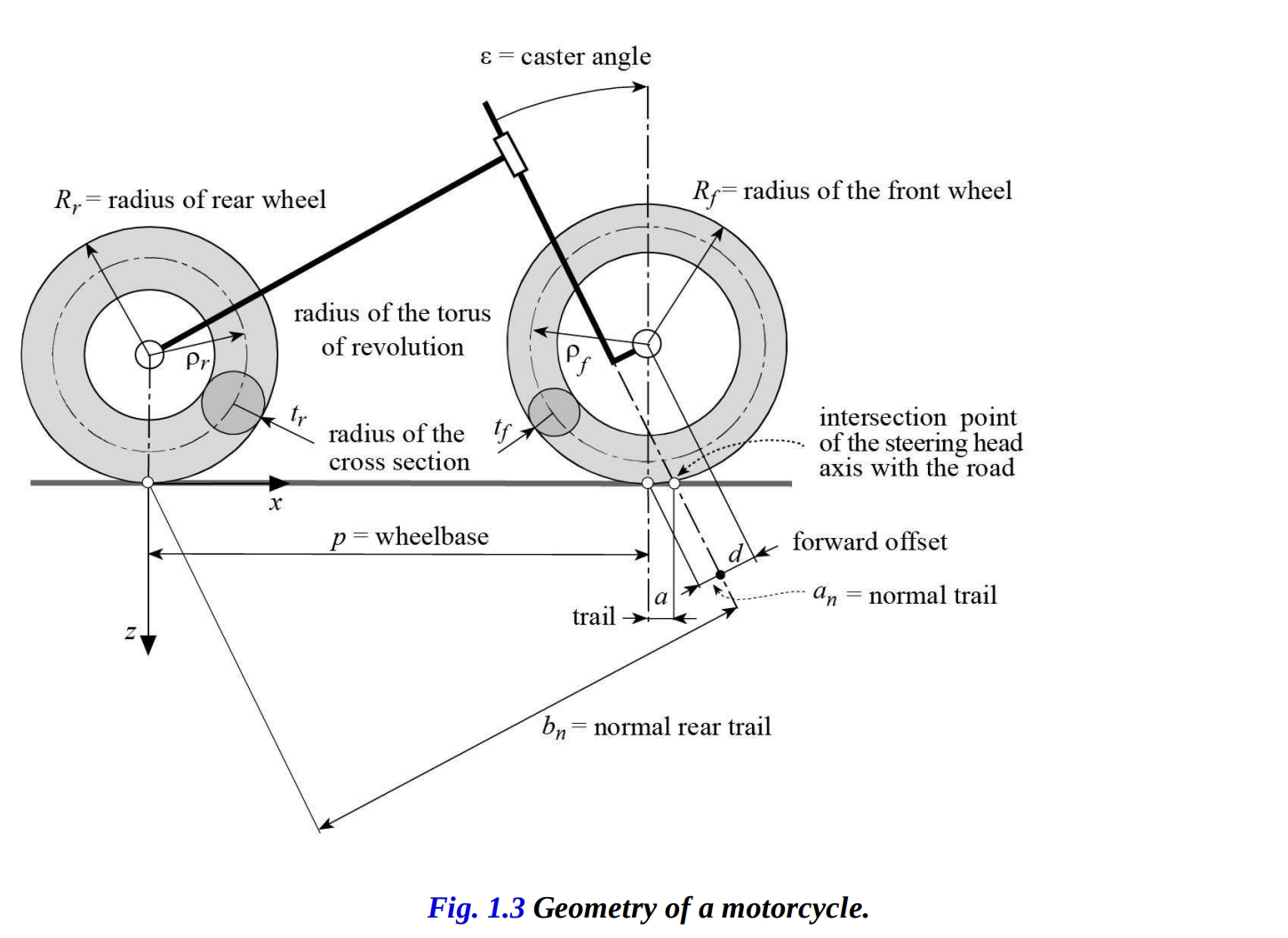
ホイールベース(p) は、路面上のタイヤの接触点間の距離です。 キャスター角(ε) は、垂直軸と前部セクションの回転軸（ステアリングヘッドの軸）との間の角度です。 トレイル(a) は、前輪の接触点とステアリングヘッド軸との交差点との間の距離で、地面平面で測定されます。

これらのパラメータは、ライダーが感じるモーターサイクルの操縦性を定義する上で重要です。ただし、これらの間に強い相互作用があるため、単独の幾何学的パラメータの効果を独立して調べることは実用的ではありません。以下では、これらのパラメータがモーターサイクルの運動学的および動的挙動にどのように影響するかについて考察します。

ホイールベースの値は、モーターサイクルの種類に応じて異なります。小型スクーターの場合は1200mmから始まり、軽量モーターサイクル（125cc排気量）では1300mm、中排気量モーターサイクル（250cc）では1350mmまで、およびそれ以上の大排気量のツーリングモーターサイクルでは1600mm以上になります。

一般に、他のパラメータが一定の場合、ホイールベースの増加は以下をもたらします：

• フレームの曲げおよび捩れ変形性の不利な増加。これらのパラメータは、操縦性に非常に重要であり、より変形しやすいフレームはモーターサイクルをより操縦しにくくします。
• 最小曲率半径の不利な増加。これにより、小さな曲率半径の経路での旋回がより困難になります。
• 旋回するために、ハンドルバーにかけるトルクの不利な増加が必要です。
• アクセルおよびブレーキングフェーズ中の二つの車輪間での負荷の移動の不利な減少により、ピッチング動作が減少し、前後の転覆（flip-over）がより困難になります。
• 路面の凹凸によって生成されるピッチング運動の不利な減少。
• モーターサイクルの方向安定性の有利な増加。

トレイルとキャスター角は、ステアリングヘッドの幾何学的特性を定義するため、特に重要です。モーターサイクルの操縦性と方向安定性の特性の定義は、他の要因の中でもこれらに依存します。

キャスター角の値は、モーターサイクルの種類によって異なります。スピードウェイでは19°、競技用またはスポーツモーターサイクルでは21〜24°、ツーリングモーターサイクルでは27〜34°です。構造的な観点から、非常に小さな角度はブレーキング中にフォークに顕著な応力を与えます。前フォークは曲げおよびねじれに対してかなり変形しやすいため、角度の小さい値は大きな応力を引き起こし、その結果、前部アセンブリの危険な振動を引き起こす可能性があります（ステアリングヘッドの軸を中心にした前部アセンブリの振動、いわゆるウォブル:wobble）。

キャスター角の値は、トレイルの値と密接に関連しています。一般的に、モーターサイクルの操縦性をよく感じるには、キャスター角の増加に対応してトレイルの増加が必要です。

トレイルの値は、モーターサイクルの種類とホイールベースに依存します。競技用モーターサイクルでは75〜90mm、ツーリングやスポーツモデルでは90〜100mm、純粋なツーリングモデルでは120mm以上になります。

1.3 トレイルの重要性

モーターサイクルの特異な点の一つは、その操舵システムであり、その機能は基本的には、例えばモーターサイクルの方向を変えたり、平衡を確保するために必要な横力の変化を生じさせることです。

この観点から、操舵システムは、前輪に垂直に配置された二つの小さなロケットからなると仮定すると、適切に活性化された場合、ライダーにとってかなりの困難や克服困難がないわけではありませんが、横力を生成し、つまり、操舵システムと同じ機能を果たすことができます。

幾何学的な観点からは、クラシックな操舵メカニズムは、次の三つのパラメータによって記述されます：

• キャスター角(ε)
• フォークオフセット(d)
• ホイールの半径(Rf)

これらのパラメータによって、法線トレイル(an)の値を計算することができます。これは、接触点とモーターサイクルの操舵ヘッドの軸との垂直距離です。これは、前輪の接触点が道路平面上でのステアリングヘッドの軸と道路自体の交差点の点よりも後ろにあるときに正と見なされます（図1-4で示されています）。先に見たように、道路上で測定されるトレイルは、次の式によって法線トレイルと関連しています：

• a = an / cos ε

トレイルの値は、特に直線運動中のモーターサイクルの安定性にとって非常に重要です。

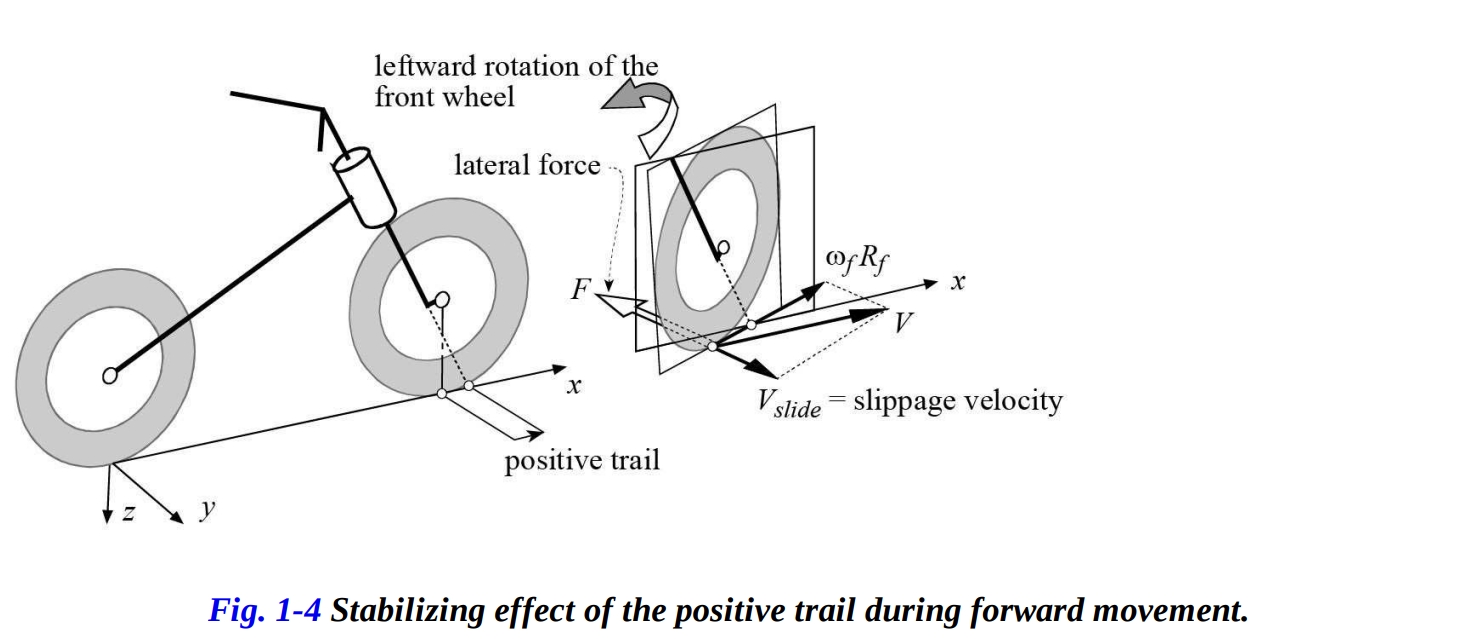
この概念を発展させるために、まずモーターサイクルが直進して一定速度$V$ で走行していると考えてみましょう。そして、道路の表面の不均一さや横風などの外部の乱れが前輪をわずかに左に回転させると仮定しましょう。当面の間は、モーターサイクルが左に旋回し始め、遠心力の影響で同時に右に傾き始めるという事実を無視し、代わりにタイヤと地面の接触によって生成される横方向の摩擦力$F$ に注目します。

言い換えると、モーターサイクルが一定速度$F$ で走行しており、前輪の接触点も同じ方向に速度$V$ を持っていると仮定しましょう。ベクトル$V$ は二つの直交成分に分解できます。

• $\omega_f R_f$ 成分は、転がりによる速度を表し、車輪の平面に配置され、ステアリング角度に依存して左に回転します。
• $V_{slide}$ 成分は、接触点の道路面に対する滑り速度を表します。

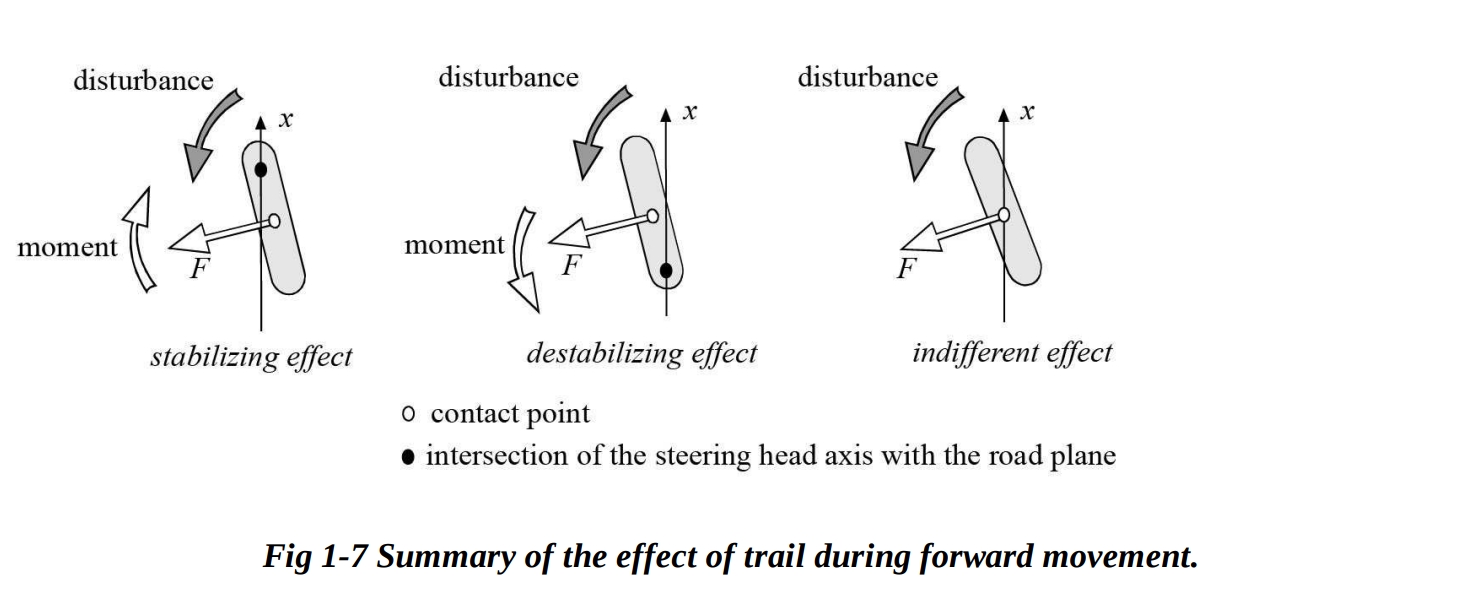
したがって、前輪に摩擦力 $F$ が作用します。 $F$ は滑り速度の方向に平行ですが、逆の向きです（図1-4を参照）。トレイルが正であるため、摩擦力$F$ は前輪を正対させるモーメントを生成します。このモーメントは、法線トレイルの値に比例します。

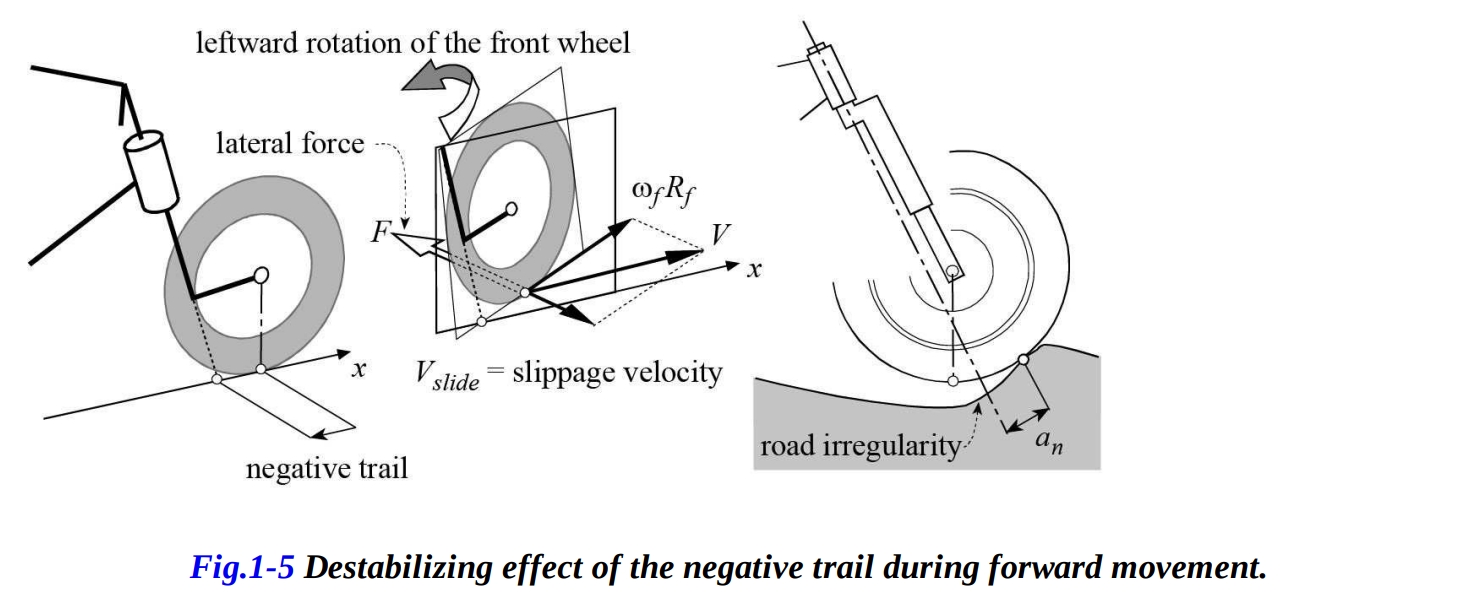
もしトレイルの値が負であれば（接触点がステアリングヘッド軸と道路面の交差点の前にある場合）、そして摩擦力 $F$ が常に滑り速度の反対方向にあると考えると、左方向への回転を増加させる向きのステアリングヘッド軸周りのモーメントが生成されるでしょう。図1-5では、摩擦力$F$ が乱れを増幅させ、モーターサイクルの平衡が深刻に損なわれることが示されています。図1-5は、道路のプロファイルが、例えばホイールが段差や凸凹を通過するときにトレイルを負にすることがあることを示しています。

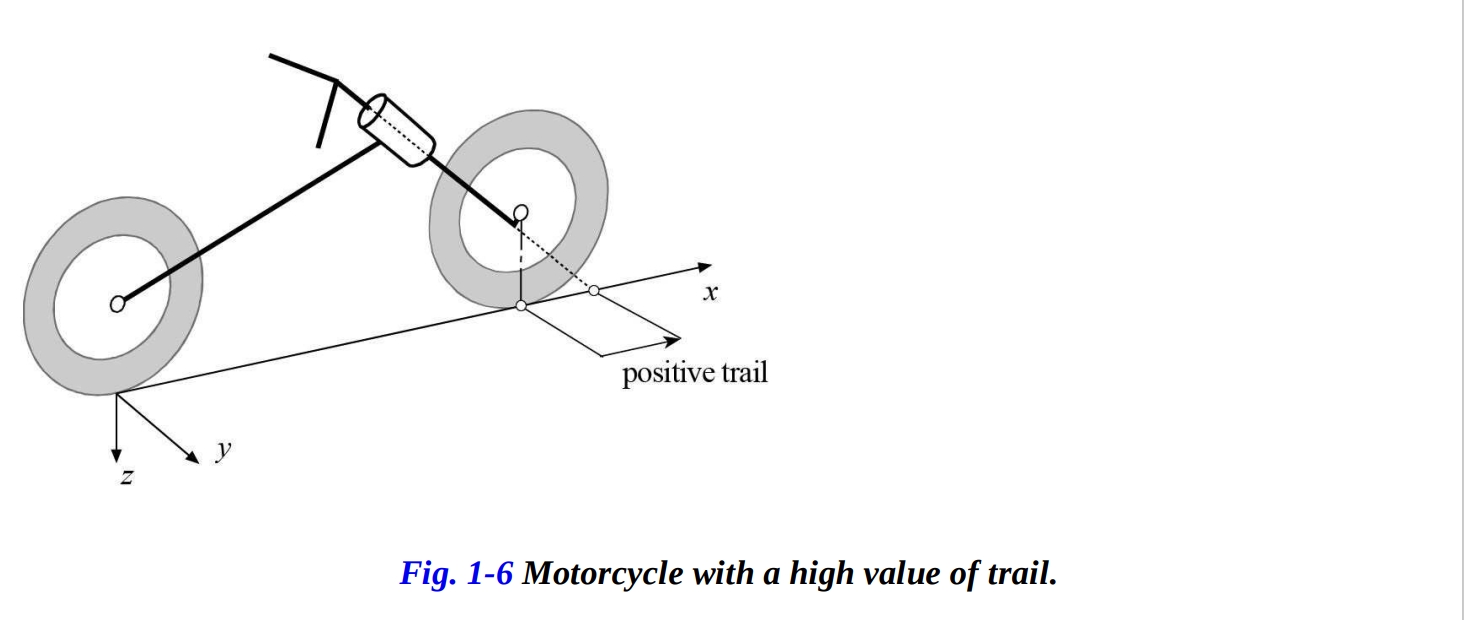
トレイル値が小さいと、横方向の摩擦力の正対モーメントも小さくなります。ライダーが操舵が容易だと感じていても、操舵メカニズムは道路の不均一さに非常に敏感です。トレイルの値が大きい場合（図1-6に示されているような大きなキャスター角でそうなる）、モーターサイクルの直進安定性が増しますが、操縦性は著しく低下します。

たとえば、「イージーライダー」という有名な映画の成功を受けて非常に人気が高まった「チョッパー」タイプのモーターサイクルを考えてみてください。これらのモーターサイクルは、キャスター角の値が40°までになることがあり、これにより曲がりくねった道路よりも直線の高速道路に適応しやすくなります。

曲線運動中、道路のグリップは、車輪平面と道路の交差線に垂直な横方向の摩擦力によって確保されます。

前輪と後輪の横方向の力は、それぞれホイールベースとトレイルに関連する距離 $a_n$ および $b_n$ に比例するモーメントを生成します。これらの距離は次の式によって表されます。

ここで、$a_n$ は前輪の法線トレイルを表し、$b_n$ は後輪の法線トレイルと考えることができます。

この単純な考察から、ホイールベースとトレイルが互いに密接に関連していることが示され、したがって一緒に考慮されるべきであることがわかります。モーターサイクルのホイールベースに言及せずに、トレイルを小さいまたは大きいと定義することは完全に正確ではありません。比較パラメータとして、前輪と後輪の正常なトレイルの比率を使用することができます。

一般的に、モーターサイクルの正常な前輪トレイルは、後輪の値の約4〜8％です。レーシングモーターサイクルのこの比率は約6％です。スポーツおよびスーパースポーツモーターサイクルでは、6から6.5％の範囲です。そして、スポーツモーターサイクルとほぼ同様のツーリングモーターサイクルでは、この比率は6から8％の範囲になります。

一方、「クルーザー」タイプのモーターサイクル（重くて遅いモーターサイクル）の特徴は、5〜6％の値を持ち、ホイールベースと比較して控えめなトレイルを持ちます。これはおそらく、低速での機動性を確保する必要があるためです。前輪への負荷が重いため、小さいトレイルを選択することで、ライダーが特定の操縦を実行するために適用するトルクの値を下げることができます。

この比率は、スクーターでもも低くされています。なぜなら、スクーターは低速で使用される（または使用すべきである）ため、直進安定性よりも機動性が優先されるからです。

厳密に言えば、比率は車輪への負荷の分布を考慮する必要があります。前輪に重い負荷がかかるモーターサイクルでは、より短いトレイルが適します。実際、前輪に重い負荷がかかると、車輪の横方向の運動に比例して大きな横方向の摩擦力が発生します。したがって、同じ正対トルクがステアリングヘッドの軸を中心に作用する場合でも、より小さなトレイルで十分なのです。 負荷分布に基づいた正しい比率は、以下の式で表されます。

ここで、$N_f$ は前輪への負荷であり、$N_r$ は後輪への負荷です。

1.4 ステアリング機構の運動解析

ハンドルを曲げる時に、モーターサイクルを完全に垂直に保っているとすると、ステアリングヘッドは下がり、ステアリング角が非常に高い値の時にのみ上昇を始めます。この現象を以下の場合で説明します。

• フォークオフセットがないステアリング機構 d = 0
• 非ゼロのフォークオフセットを持つステアリング機構 d ≠ 0

1.4.1 フォークオフセットがないステアリング機構

フォークにオフセットがない場合、ホイールの中心はステアリングヘッドの軸上にあります。以下の仮定を追加しましょう：

• モーターサイクルのロール角度はゼロです。
• ホイールの厚みはゼロです。

図1-8に示すように、ステアリング角δがゼロの場合、ホイールは完全に垂直でxz平面にあります。

キャスター角ε、ステアリング角δ、前輪のキャンバー角β、運動学的ステアリング角Δ（回転角δを道路平面上に射影した角度）、および角度αは、以下の三角関数の方程式を通じて関連付けられます。

これらの前提条件から、$\sin \alpha$ と $cos \alpha$ を δ と ε の関数として導くことが可能です。

次に、ホイールの中心（点 $O$ ）が上昇したり下降したりしないと仮定します。前輪の $\delta$ 回転により、ホイールは垂直位置に対して傾斜し、水平面 $xy$ から離れます。ホイール中心の道路面からの距離 $OD$ は、ホイールの半径 $OP$ よりも大きくなります。

実際には、ホイールは地面から持ち上げられるのではなく、むしろ下げられます。ステアリングヘッドの軸を不動のままにしていると仮定すると、ホイールの中心はステアリングヘッドの軸に沿って点 $O_1$ に移動します。したがって、接触点 $P_1$ は図 1-8 に示されているように前方に移動します。最終的な位置では、距離 $OP$ は明らかにホイールの半径 $OP$ に等しくなります。

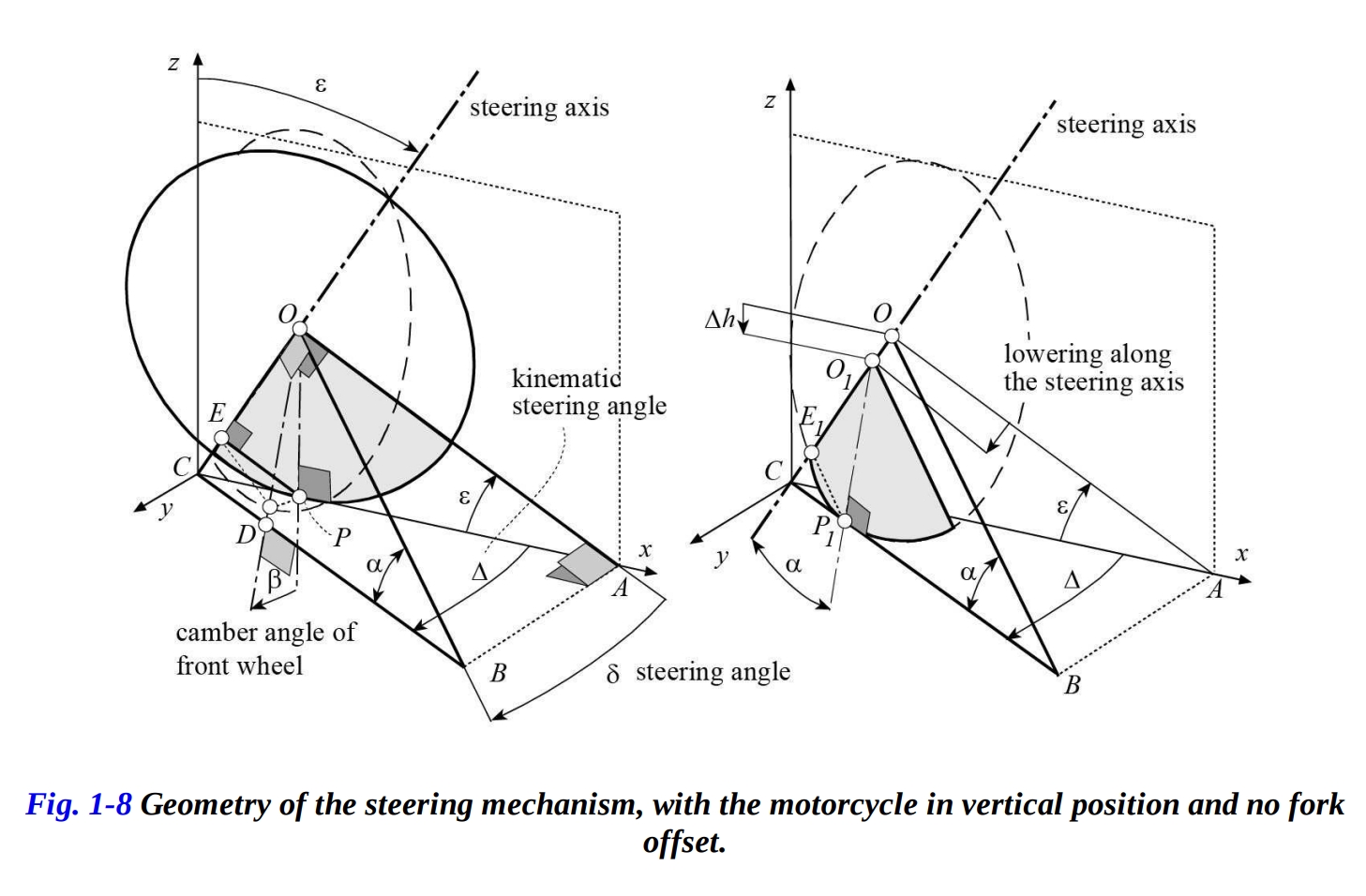
ステアリング角がゼロの場合（図1-8、左）、法線トレイルと道路面で測定されるトレイルは次のようになります。

ここで、$R_f$ は前輪の半径です。ステアリング角 $δ$ がゼロでない場合、法線トレイル
$a_n = P_1 E_1 = R_f \sin \alpha$ を整理すると、次に式になります。

道路面で測定されるトレイルは、法線トレイルとステアリング角 $\delta$ による次の式で表されます。

ホイール中心の垂直変位（$\Delta h$ ）は、次の差によって与えられます。

角度 $\alpha$ を $\delta$ と ε の関数として表すと、以下のようになります。

1.4.2 フォークオフセットのあるステアリング

さて、オフセット $d$ 、つまりホイールの中心とステアリングヘッド軸との距離の影響を考えてみましょう。ゼロオフセットの場合に角度 $\delta$ と ε の関数としてステアリングヘッドの下降を表現することを許容した考察は有効ですが、オフセットがあるためにゼロオフセットの式を修正する必要があります。なぜなら、オフセットによってホイールの中心 O が O* に移動するからです。これは図1-9に示されています。

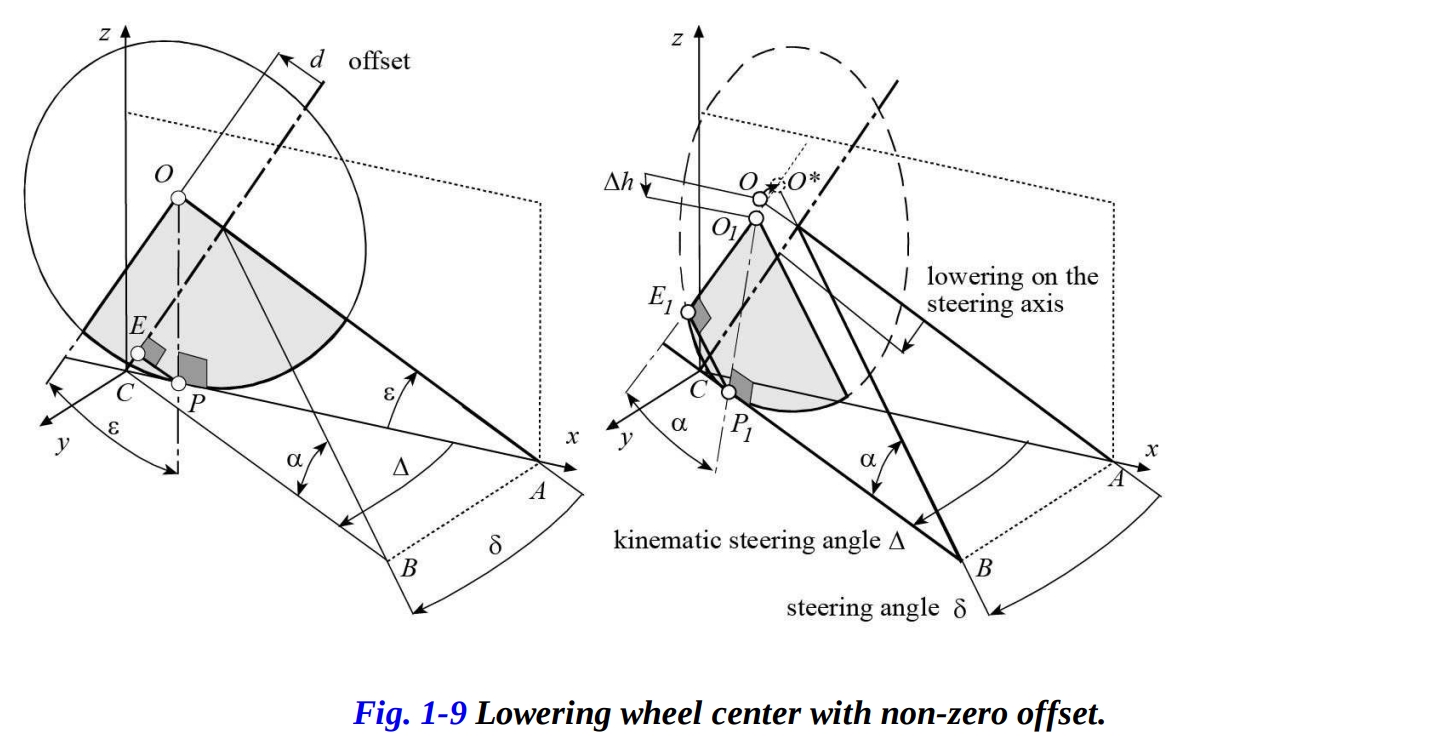
ゼロのステアリング角度では、トレイルは次のようになります：

非ゼロのステアリング角度 $\delta$ の場合、トレイルは次のようになります。

フォークオフセットが存在すると、ホイールの下降値に $d \cdot \sin ε \cdot (1 - \cos \delta)$ の減少が生じます。この値は、オフセットを考慮せずに計算されたフロントアクスルの下降値から差し引かれる必要があります。

結論として、オフセットがある場合、ゼロオフセットの場合よりも、フロントホイールの中心の下降値が少なくなります。

例1：

次のステアリングパラメータを持つバイクを考えます：

• 前輪の半径：$R_f = 0.3 m$
• オフセット：$d = 0.05 m$
• キャスタ角：$ε = 27°$

ステアリング角$\delta = 9°$ の場合、次のようになります：

• ゼロオフセットの場合：$\Delta h = 0.75 mm$
• オフセット付きの場合：$\Delta h = 0.478 mm$

ステアリング角を$\delta = 45°$ に増やすと、次のようになります：

• ゼロオフセットの場合：$\Delta h = 1.59 mm$
• オフセット付きの場合：$\Delta h = 0.92 mm$

この例は、オフセットを無視すると前輪中心の下降値を計算する際に大きな誤差が生じることを示しています。ステアリングの範囲は一般的に ±35°未満であることに注意する必要があります。

例2：

同じ機械トレール（$a = 101 mm$ ）、同じ半径（$R_f = 0.3 m$ ）、異なるキャスタ角（$ε_1 = 27°, ε_2 = 20°$ ）を持つ2台のバイクを垂直位置に考えます。

ステアリング角が0°から9°に変化した場合、各キャスタ角の前輪中心の下降値を計算します。

• $ε_1 = 27°$ および$\delta = 9°$ の場合：$\Delta h = 0.50 mm$
• $ε_2 = 20°$ および$\delta = 9°$ の場合：$\Delta h = 0.40 mm$

低いキャスタ角は、前輪中心の下降値を減少させます。

ステアリング角$\delta$ が 9°の場合、各キャスタ角に対するトレールの変化を計算します。

• $ε_1 = 27°$ および$\delta = 9°$ の場合：$a = 99.5 mm$
• $ε_2 = 20°$ および$\delta = 9°$ の場合：$a = 99.8 mm$

トレールの値は、わずかにステアリング角に依存します。

これまでの考察により、ステアリングヘッドの下降値とトレールの値を$\delta$ と ε の角度で表す解析方程式を見つけることができました。これは、ロール角度がゼロであり、前輪の厚みがゼロであるという限定的なの仮定を考慮しています。次のセクションでは、より複雑な運動モデルが使用され、ロール角度と前輪タイヤ断面の半径の両方を考慮しています。

1.5 ロール運動とステアリング

2輪車の運動解析は4輪車よりも複雑であり、いくつかの独特な側面も持ちます。

例えば、ある点で直線運動中の速度Vのバイクを考えてみましょう。そのバイクがある時点でカーブに入るとします。バイクはステアリング角度がゼロの直立姿勢から、ロール角$\phi$ を持つ傾斜した姿勢に移行します。バランスを保つために、ハンドルバーの回転角度は、カーブの半径と速度に応じてゼロのままではいられなくなります。

我々は、車輪の厚さがゼロであると仮定すると、ステアリングの回転が、ステアリングヘッドのわずかな下降を引き起こし、その結果、後部フレームが後輪の軸周りにわずかな前方回転を生じることを見てきました（ピッチ回転）。

それでは、実際にはロール運動に従って、後輪の接触点がどのように変位するかを見てみましょう。ここでは、次の2つの三角形を定義できます。

• 動的な三角形（$P_r,x,y,z$ ）は、自動車技術者協会（SAE）によって指定されたように定義されます。原点は後輪の接触点 $Pr$ に設定されます。軸 $x$ は水平で後輪の平面と平行です。軸 $z$ は垂直で下向きに向いており、軸 $y$ は道路面に平行です。したがって、道路の表面は平面$z = 0$ で表されます。
• 後部フレームに固定された三角形（$A_r,X_r,Y_r,Z_r$ ）は、バイクが完全に垂直でステアリング角度δがゼロの場合にSAEの三角形と重なります。

今、後輪のみがロール角 $\phi$ で傾いていると仮定しましょう。その結果、後軸に固定された三角形（$A_r,X_r,Y_r,Z_r$ ）が $x$ 軸を中心に同じ角度で回転します。したがって、三角形の原点 $A_r$ は $P_r$ に対して平行移動します（図1-11bを参照）。

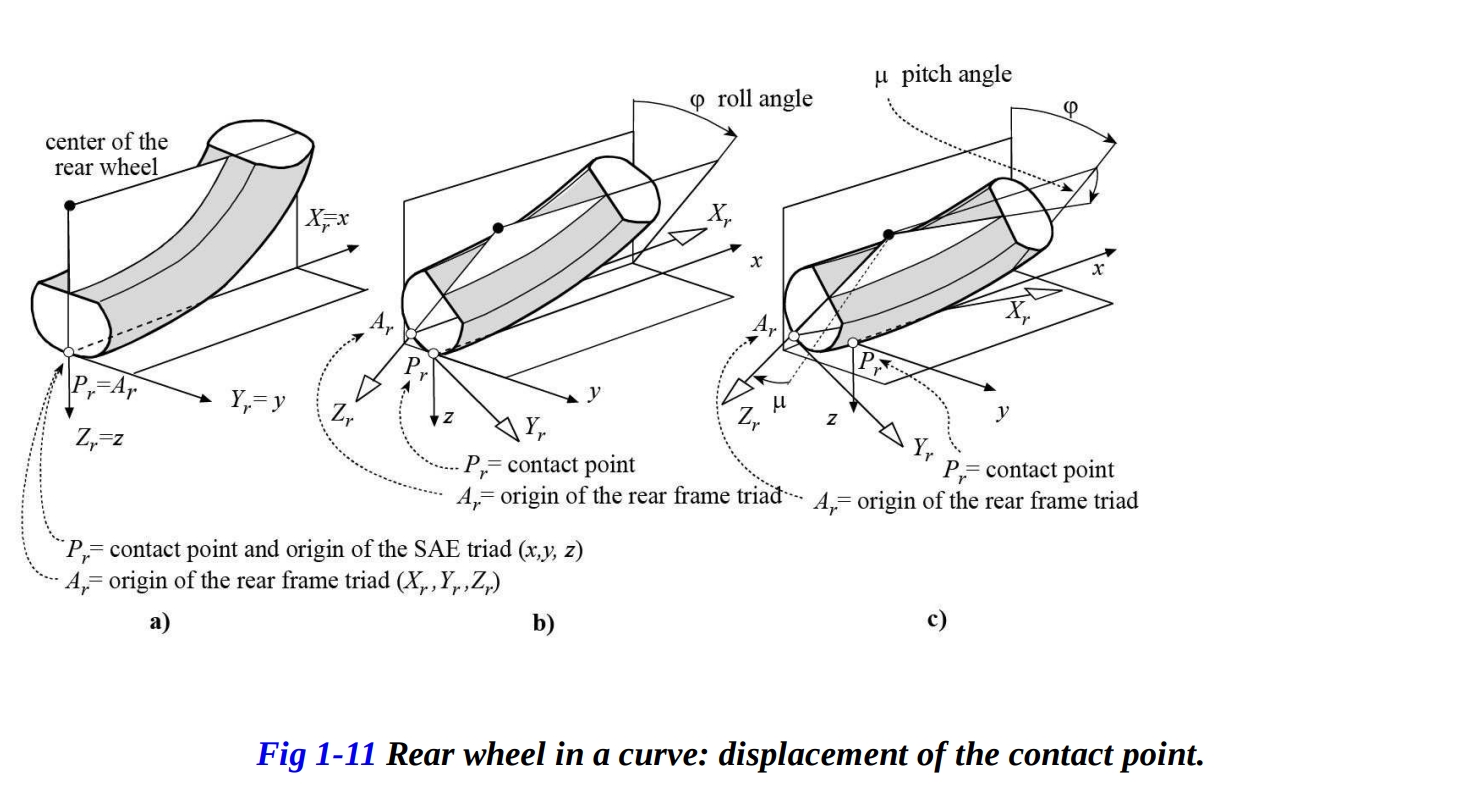
ステアリングヘッドの下降によって、後部フレームのわずかなピッチング回転が生じることが分かります。言い換えれば、後部フレームに固定された三角形の別の回転が生じます（図1-11cを参照）。

重要なのは、三角形の原点$A_r$ が後部フレームに固定されていることであり、後輪に固定されているわけではないことです。すなわち、$A_r$ はロール角 $\phi$ とピッチ角 $\mu$ が両方ゼロの場合にのみ $P_r$ と一致します。

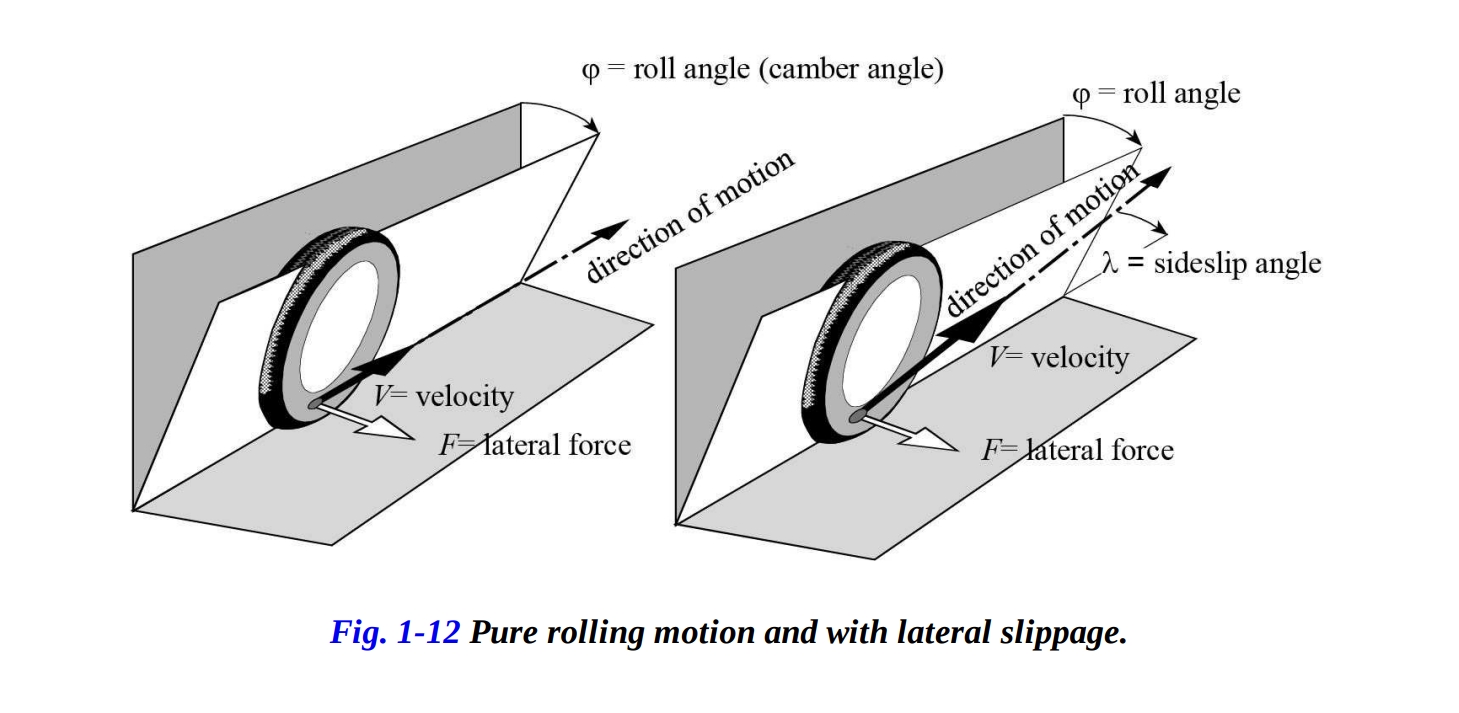
前輪の挙動はさらに複雑です。なぜなら、ローリングとピッチング運動に加えて、前輪はステアリングヘッドの軸周りにも回転します。傾斜した位置から垂直な位置への変化は、タイヤと道路面の間の滑りがゼロであるかのように、純粋なロール運動であると仮定されました。しかし、現実には挙動はより複雑です。曲線上で側方反応力を生成するためには、横滑り角 $\lambda$ の観点から側方のスリップが必要かもしれません（次章では、タイヤに関する内容で、スリップは車輪のキャンバー角によって生成される力の値に応じて正または負になることが示されます）。図1-12は、純粋なローリング運動と側方スリップを伴う運動の場合を示しています。スリップがない場合、車輪の接触点の前方運動の速度ベクトルが、バイクが曲線を走行していても、車輪自体と平行な平面にあることを意味します。

1.6 モーターサイクルのピッチ

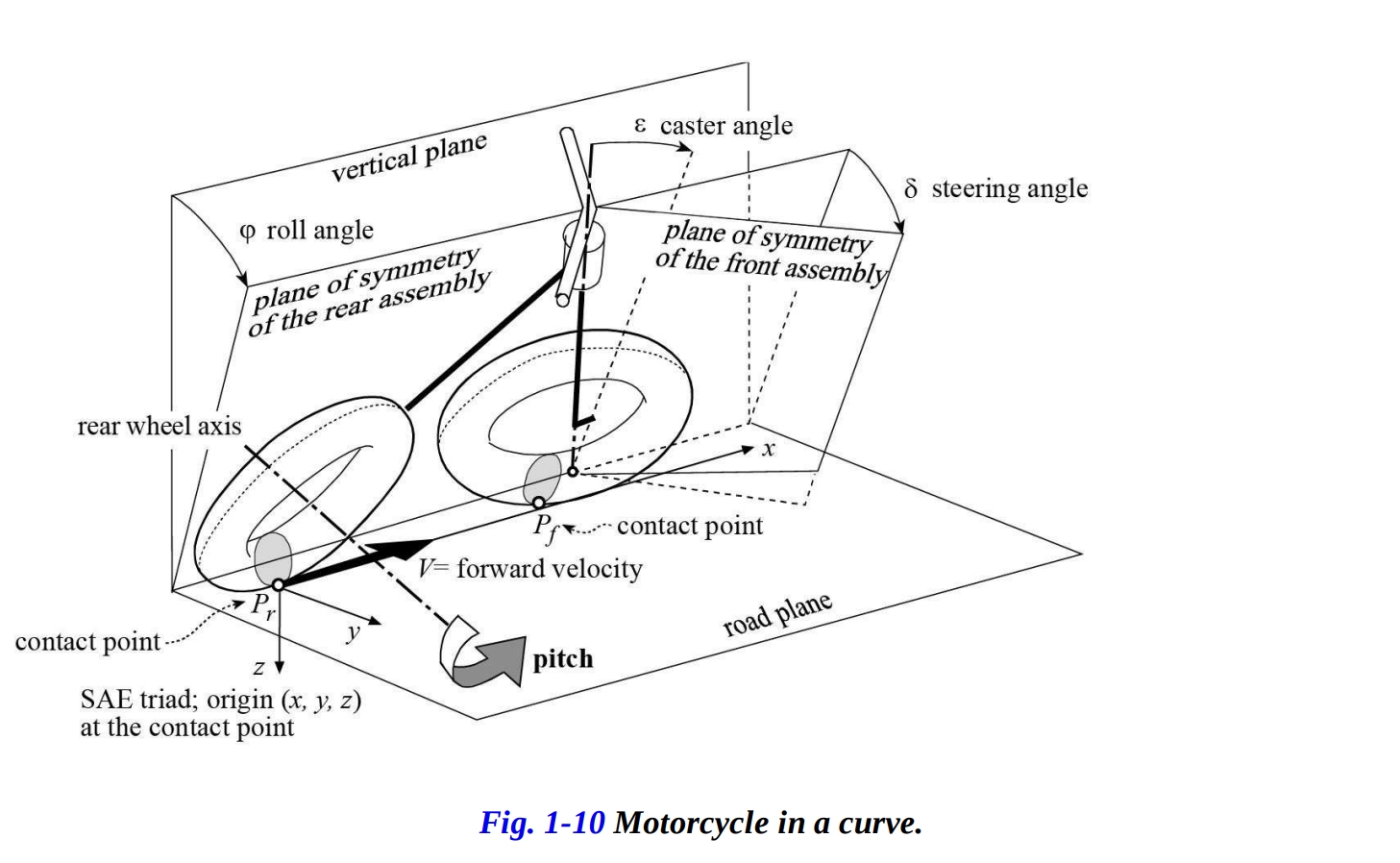
前述のように、モーターサイクルが完全に垂直な状態（$\phi = 0$ ）であるとき、ハンドルバーの回転によって前輪の中心が下がり、それによって後部フレームが後輪の軸を中心に回転することを示しました。言い換えれば、ハンドルの動きがピッチング運動を引き起こします。これから、より一般的なケースでのモーターサイクルのピッチを考察し、ゼロ以外のロール角 $\phi$ とタイヤ断面のサイズを考慮します（図1-10を参照）。

フレームのピッチ角 $\mu$ は、反時計回りの方向を正としています。したがって、前輪の中心が下がるとピッチ角の値は負になります。モーターサイクルの運動解析により、次のような非線形方程式が未知のピッチ角 $\mu$ を既知の値と結びつけます。これらの既知値には、ロール角 $\phi$ 、ステアリング角 $\delta$ 、ホイールベース $p$ 、タイヤの断面半径 $t_f$ と $t_r$ 、トーラス中心円の半径$\rho _r$ と$\rho _f$ 、およびキャスタ角 ε が含まれます。

ここで:

• $c1 = d \sin ε (1 − \cos \delta) + t_r - t_f$
• $c2 = \rho _f [\cos ε \cos(\beta'−ε) - \cos \delta \sin ε \sin(\beta − ε) - 1]$
• $c3 = d \sin \delta + \rho _f \sin \delta \sin(\beta' − ε)$
• $c4 = p - d \cos ε (1 - \cos \delta)$
• $c5 = \rho _f [\sin ε \cos(\beta' − ε) + \cos \delta \cos ε \sin(\beta' − ε)]$

角度 $\beta'$ の物理的意味については、1.7.2節の図1-22で後述します。

この前述の方程式は、ピッチ角 $\mu$ が通常 20° から 35° に変動するキャスタ角 ε と比較して、その値が数度しかないため、ε に対するピッチ角 $\mu$ を無視して導出されました。

ピッチの値がわかれば、それによって前輪中心の下降値を容易に計算できます。これは、ピッチ角とホイールベースの積から得られることが多いです。

前述の方程式は、小さなステアリング角度 $\delta$ （$\sin \delta \approx \delta$ ）を考慮すると大幅に簡略化されます。この場合、ピッチの式は次のようになります。

ピッチは、幾何学的パラメータ（$a_n - t_f \sin ε$ ）に比例し、これはトーラス中心円の円軸との対応で測定される理想的な正常トレールに対応します（図1-13参照）。また、ピッチはタイヤ断面の半径の差（$t_r - t_f$ ）にも依存します。すなわち、推進中の接地性を向上させるためにリアにより大きなタイヤを装着する必要があるとき、ステアリングヘッドの下降効果が増します。第二項がステアリング角度 $\delta$ に依存せず、ロール角度 $varphi$ のみに依存することに注意する価値があります。

また、タイヤの厚みも無視する場合、つまり車輪の厚みがゼロ（$t_r = t_f = 0$ ）の場合、次の簡単な方程式が得られます：

この後者の式からわかるように、法線トレールがピッチング運動に最も大きな影響を与えるパラメータであることが示されています。

1.6.1 ステアリングおよびロール角度に関するピッチ

図1-14は、ステアリング角度 $\delta$ とロール角度 $\phi$ がピッチ角 $\mu$ に与える影響を示しています。重要なのは、ピッチ角 $\mu$ の負の値が、車両をリアホイールの軸周りに下向きに回転させることに対応するということです。したがって、ピッチ角μの負の値は、オートバイの重心を下げることになります。

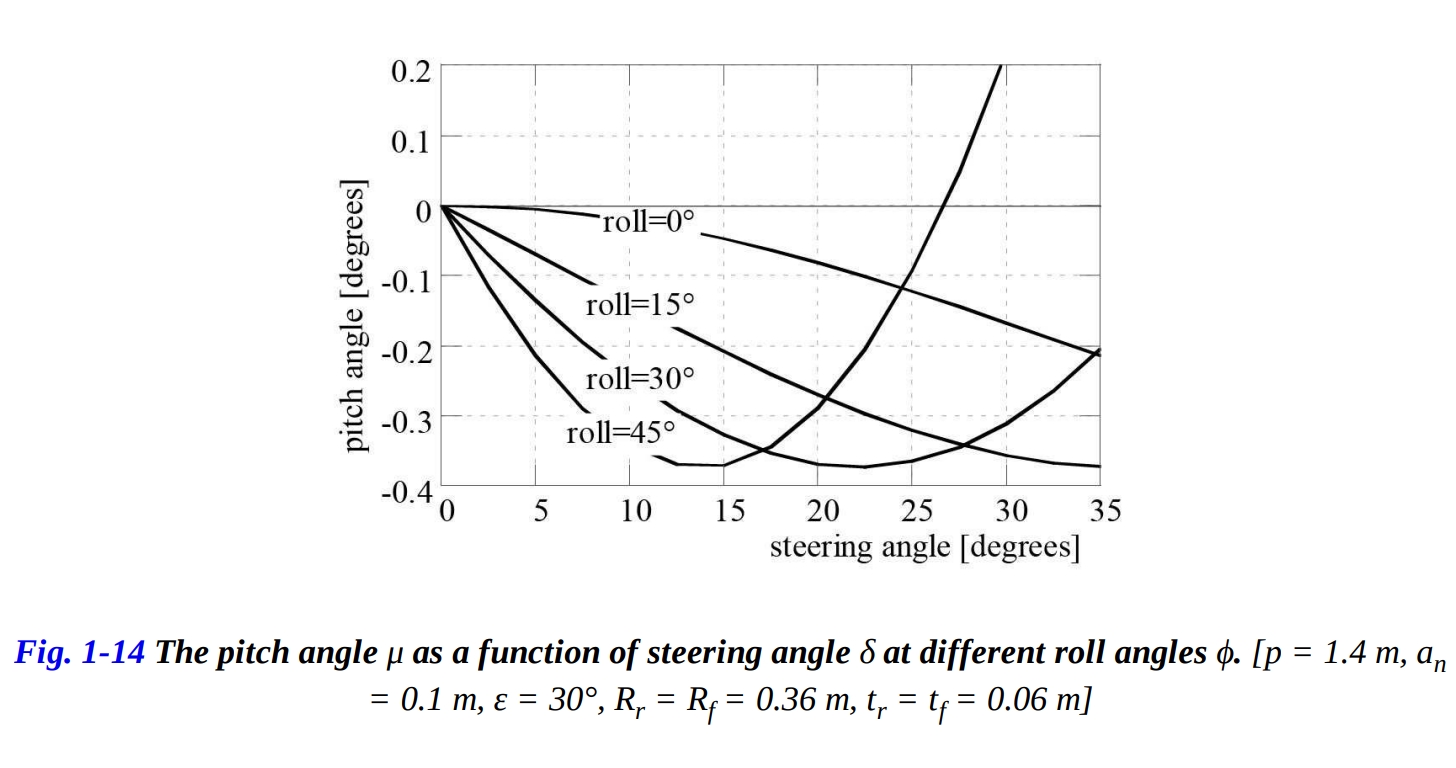
ロール角度ϕの値が高くない場合（図1-14の0°および15°）、ステアリング角度δの増加により、オートバイの重心 $G$ が連続して下がります。下がりはポテンシャルエネルギーの減少に対応するため、ステアリング角度の増加は、ハンドルにトルクをかけなくても自然に起こります。

この振る舞いは、特に自転車などの軽量な二輪車では簡単に確認できます。自転車が傾いたとき、強制されるロール角度は、ハンドルが自然に回転する角度を決定します。ロール角度の高い値（図1-14の30°および45°）では、ピッチ角 $\mu$ の変化はステアリング角度 $\delta$ に関して減少が停止し、最小値を示します。この時点で、ピッチの傾きが符号を反転させる限界値のステアリング角度 $\delta$ に到達します。

さて、ピッチ角μの最小条件を考えてみましょう。これは、ポテンシャルエネルギーの最小値（重心が最も低い位置にある）に対応します。物理的な観点から見ると、特定のロール角度 $\phi$ が課せられ、ハンドルに外部トルクが加えられない場合、前部フレームは自然にピッチ角 $\mu$ の最小値に対応するステアリング角度 $\delta$ に向かって回転しようとします。

結論として、ロール角度 $\phi$ が徐々に増加するにつれて、ピッチ角 $\mu$ の最小値はより低いステアリング角度 $\delta$ に対応します。

1.6.2 キャスター角度の関数としてのピッチ

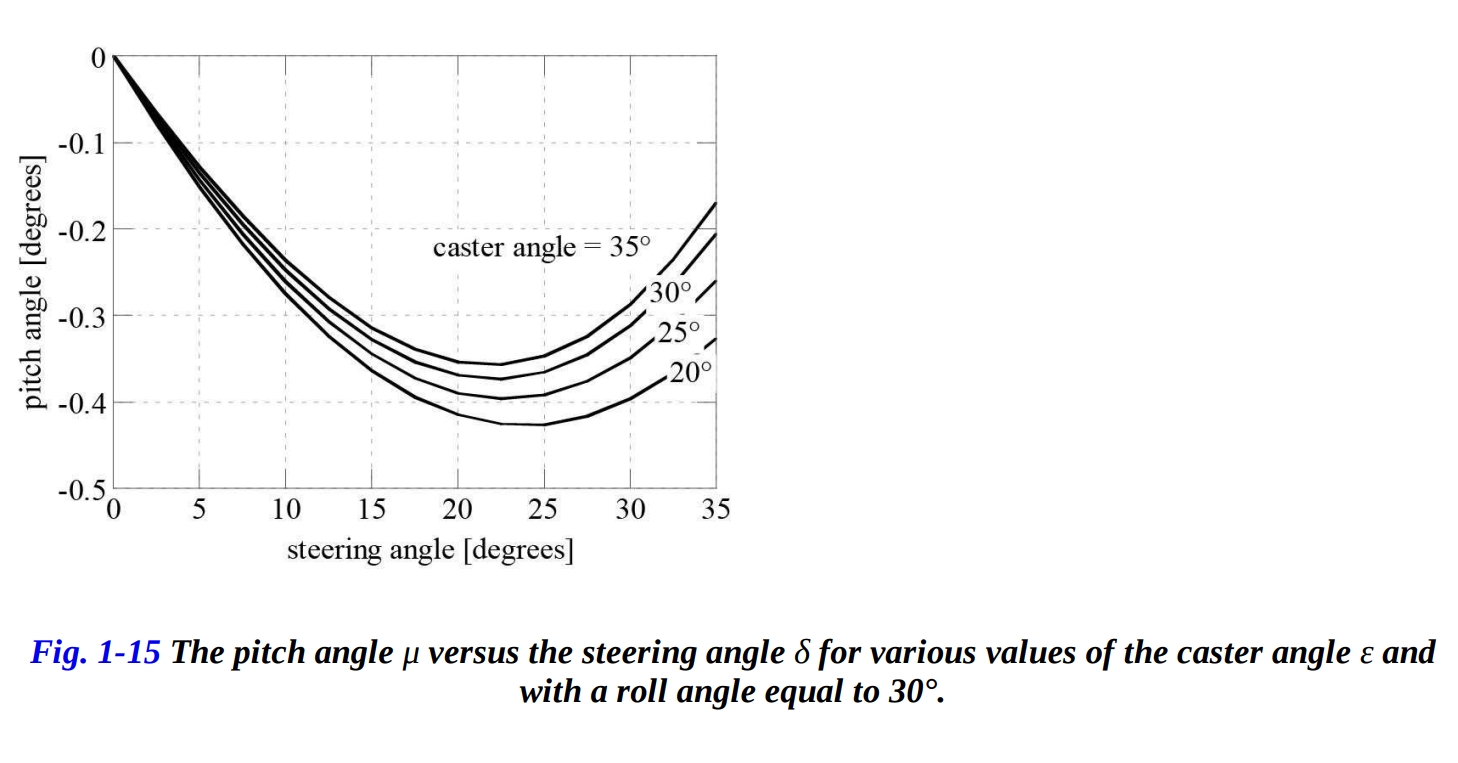
図1-15は、固定されたロール角度 $\varphi$ に対するステアリング角度 $\delta$ とステアリングヘッド角度 ε の影響を示しています。

ピッチ角 $\mu$ は、ステアリング角度 $\delta$ が増加するにつれてより負になります。キャスター角の影響は控えめです。

1.6.3 ピッチと法線トレイルの関数としてのピッチ

図1-16は、法線トレイルがオートバイのピッチに最も影響を与えるパラメータであることを示しています。 たとえば、ステアリング角度 $\delta$ が10°の場合、オフセットを変更して正規トレイルを20%変化させると、ピッチ角の変化は約35%です。

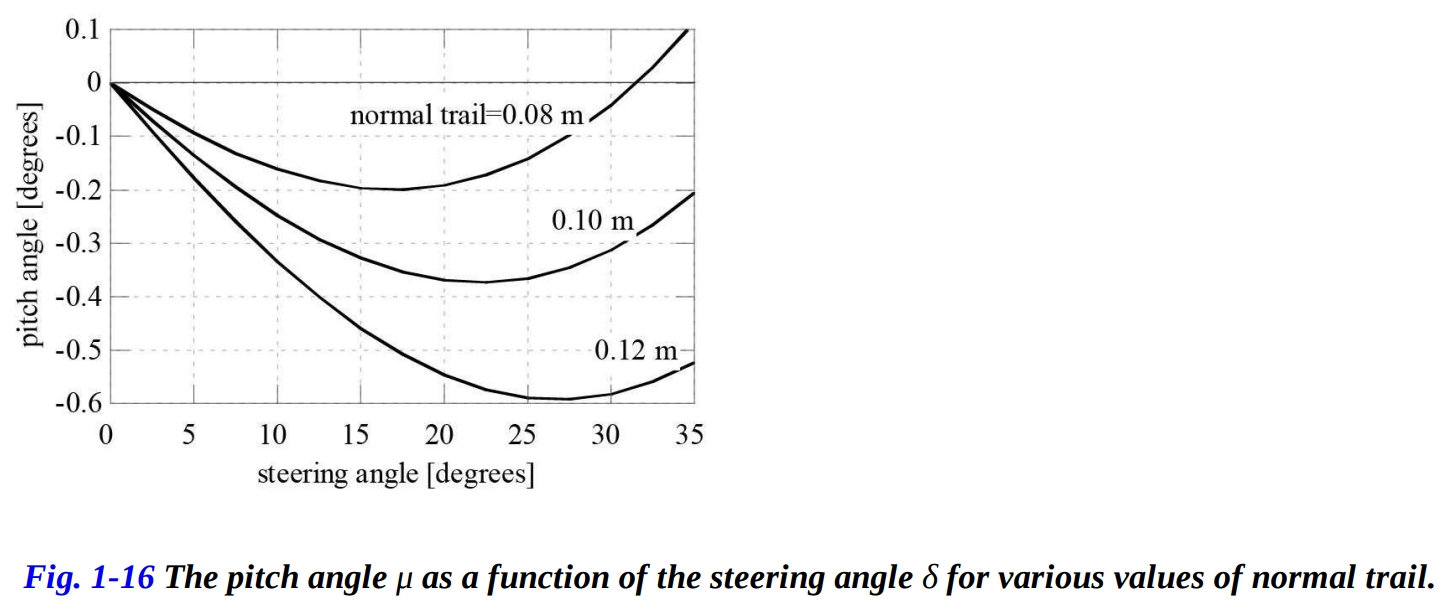
図1-16に示されているように、正規トレイルが増加すると、ピッチ角 $\mu$ の最小状態はステアリング角の増加する値に対応します。これは、ロール角が増加する場合とは逆であり、図1-16と図1-14を比較することで明らかになります。

1.7 リアホイールの接点

1.7.1 キャンバーとタイヤ断面の影響

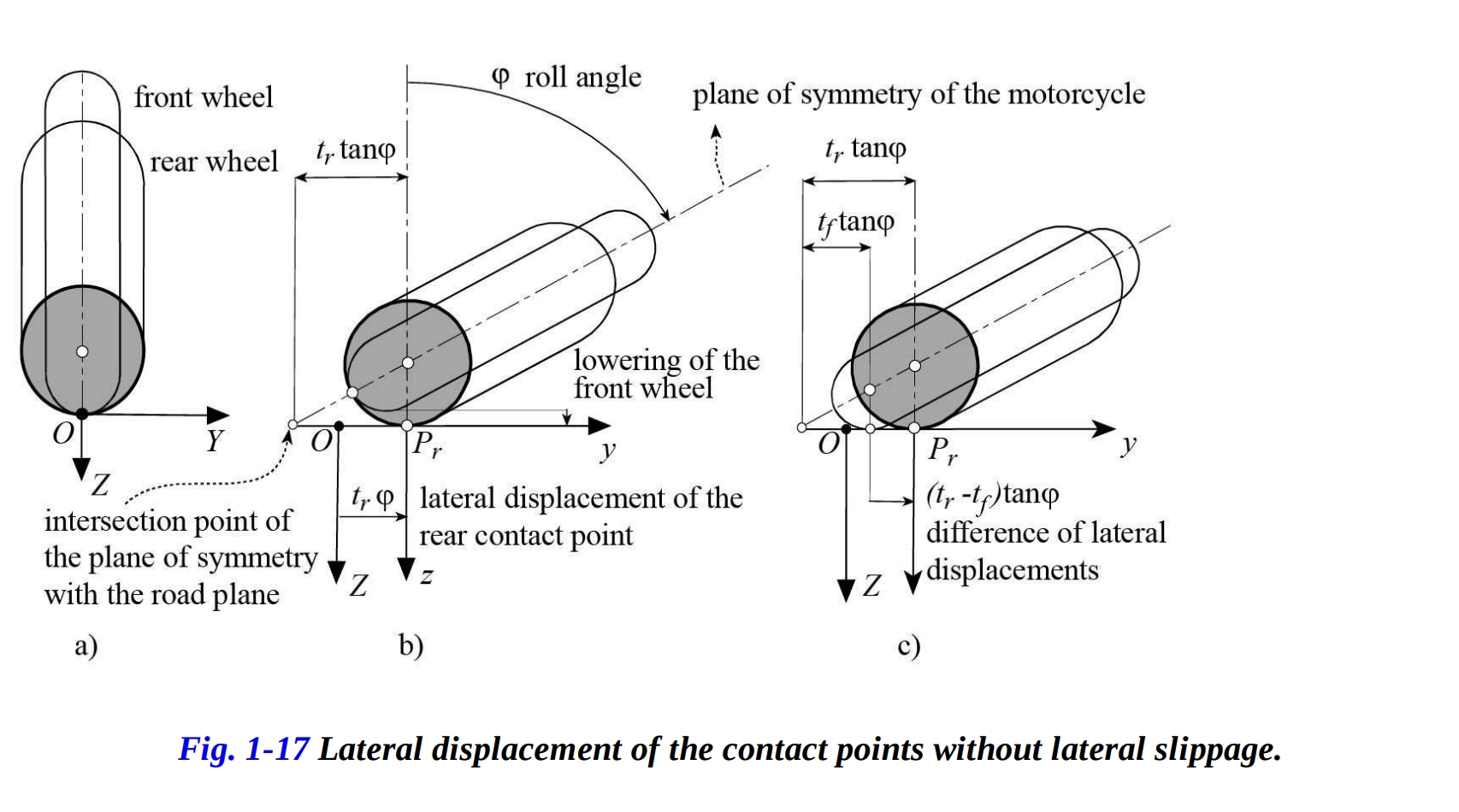
まず、垂直な位置にあるバイクを考えましょう。後輪タイヤの断面積が前輪よりも大きいとします。後部フレームが傾き、道路面で側方のロールが生じると仮定します。この時横滑りは無視します。（図1-17b）

後輪タイヤの接点は、後輪フレームのロール角とタイヤ断面の半径に比例する距離 $t_r \cdot \varphi$ だけ、$y$ 方向に側方に移動します。

後輪フレームのロール運動が起こる間、ステアリング角をゼロのままにし、バイクが後輪の軸を中心にピッチングしないと仮定しましょう。前輪が後輪よりも小さい断面を持っているため、ロール運動に応じて前輪が道路面から持ち上げられるでしょう。しかし、バイク全体が後輪の軸を中心に同時にピッチ回転することで、前輪が道路との接触が確保されます。

ロールとピッチの回転が発生した後、前輪の接触点は $(t_r - t_f) \tan \varphi$ ) だけ、後輪の接触点の左に移動します（図1-17c）。両方のタイヤが同じ断面を持つ場合、2つの接触点の側方移動量は同じです。

1.7.2 ロールとステアリングの組み合わせ効果

ハンドルの回転は、前輪の接触点の側方および縦方向の変位を生成します。

まず、垂直な姿勢のバイクを考えましょう。バイクはロール角度 $\varphi$ で傾斜し、その後ハンドルバーを角度 $\delta$ だけ回転させます。この操作により、前輪の接触点 $P_f$ が後輪フレームの平面から離れます。

点 $P_f$ の座標は、以下のSAEで定義された方程式で表されます。

c1からc5の量は、1.6節で定義されています。

図1-19は、4つのロール角度と対応するステアリング回転のための、前方接触点の側方および縦方向の変位を示しています。 ステアリング角度δと事前に設定されたロール角度φが増加すると、点は前方に移動します。図1-19は、x座標が車輪ベースと等しい初期値から増加する様子を示しています。 点は最初に左に移動します（$P_f$ のy座標は最初に負です）が、その後右に戻り、$x$ 軸を超えます（$P_f$ の $y$ 座標が符号を変えます）。通過点では、事前に設定されたロール角度 $\varphi$ が増加するにつれて、ステアリング角度 $\delta$ が減少します。

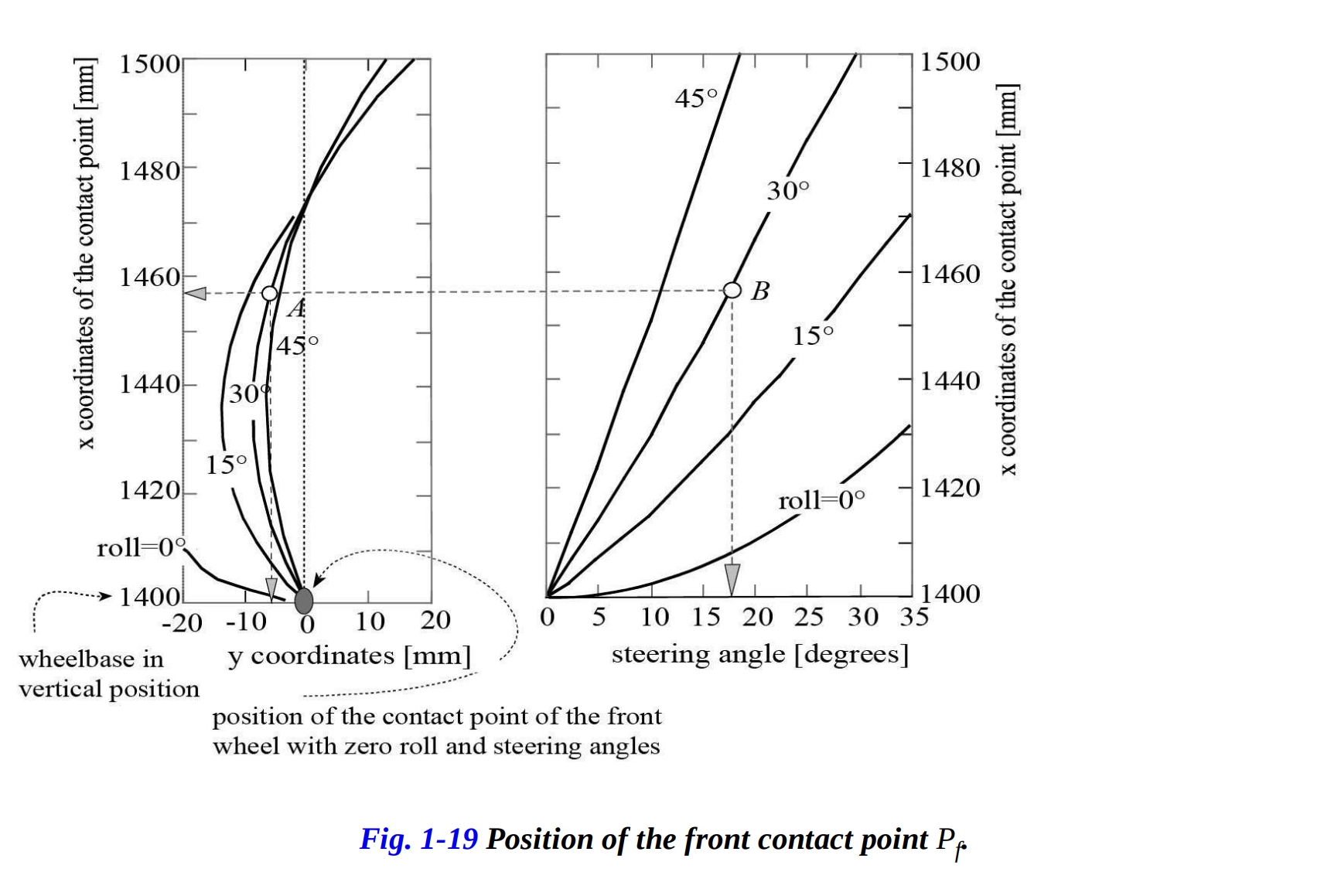
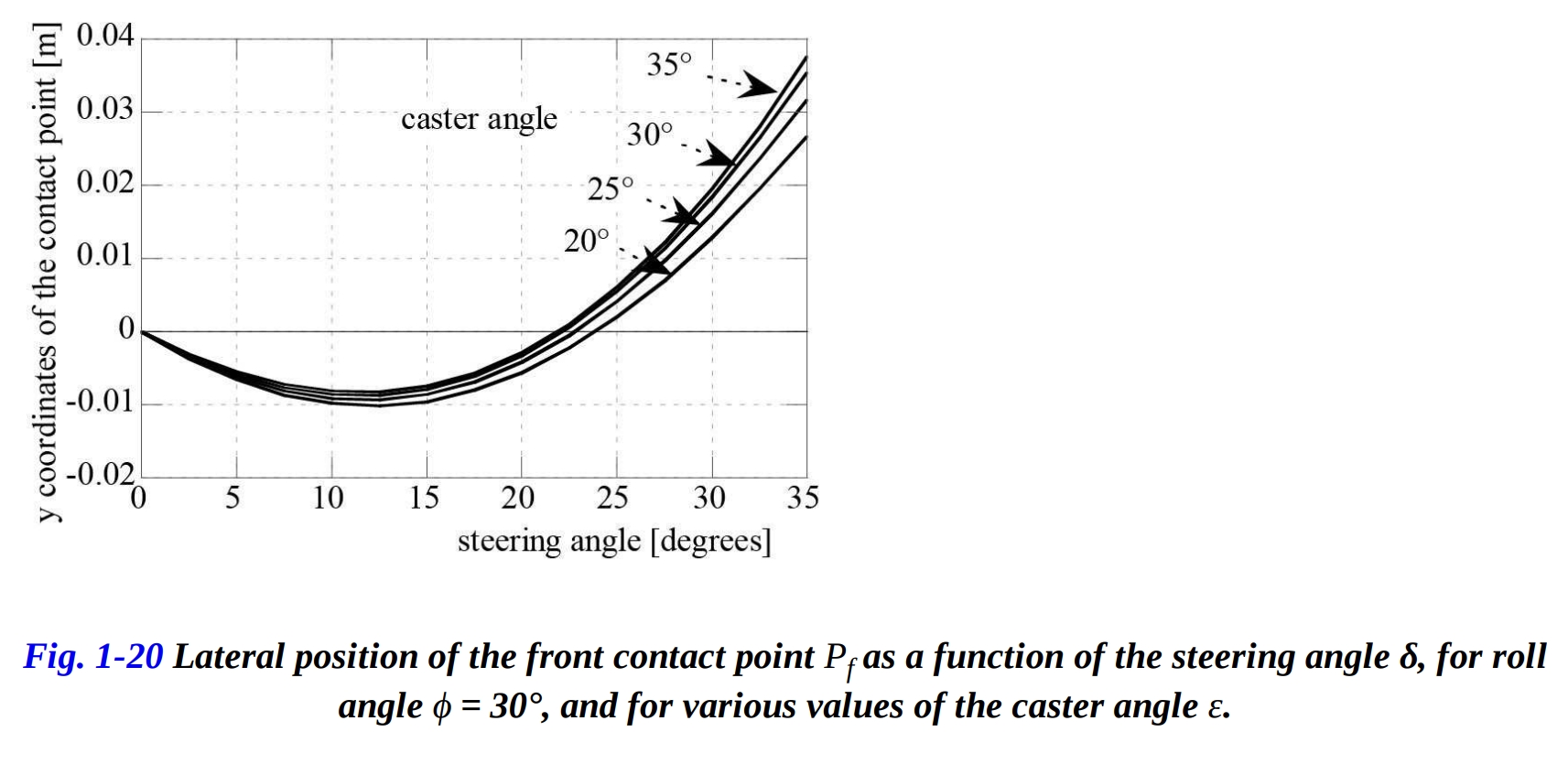
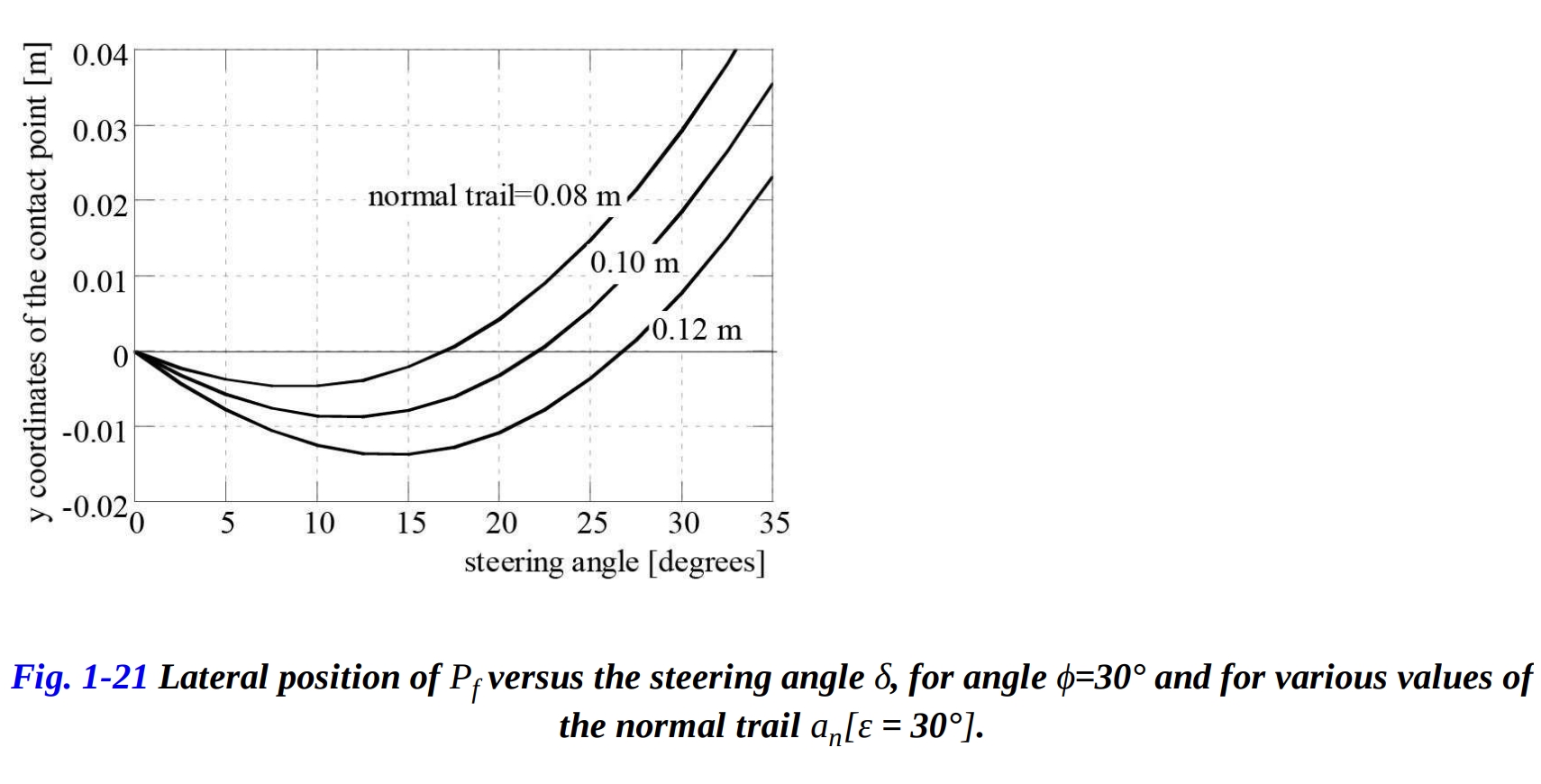
これは、キャスター角 ε の変化が接点 $P_f$ の横方向への変位に大きな影響を与えないことを示しています（図1-20）。一方で、法線トレイル $a_n$ の値の変化が接点 $P_f$ の横方向への変位に大きな影響を与えることが分かります（図1-21）。

フロントフレームに固定された状態のフロントコンタクトポイントの変位を観察するために、タイヤの厚さをゼロとした状態を考えます（図1-22）。バイクが完全に垂直であるとき（ロール角とステアリング角がゼロであるとき）、接点は $A$ にあります。図1-22に示されているように、ロール角とステアリング角を増やすと、接点Pfは $AC$ の弧に沿って移動し、その制限位置Cに達します。接点 $P_f$ がポイント $C$ に達するのは、ロール角 $\varphi$ が90°であるとき、つまり、バイクが水平であるときだけです。

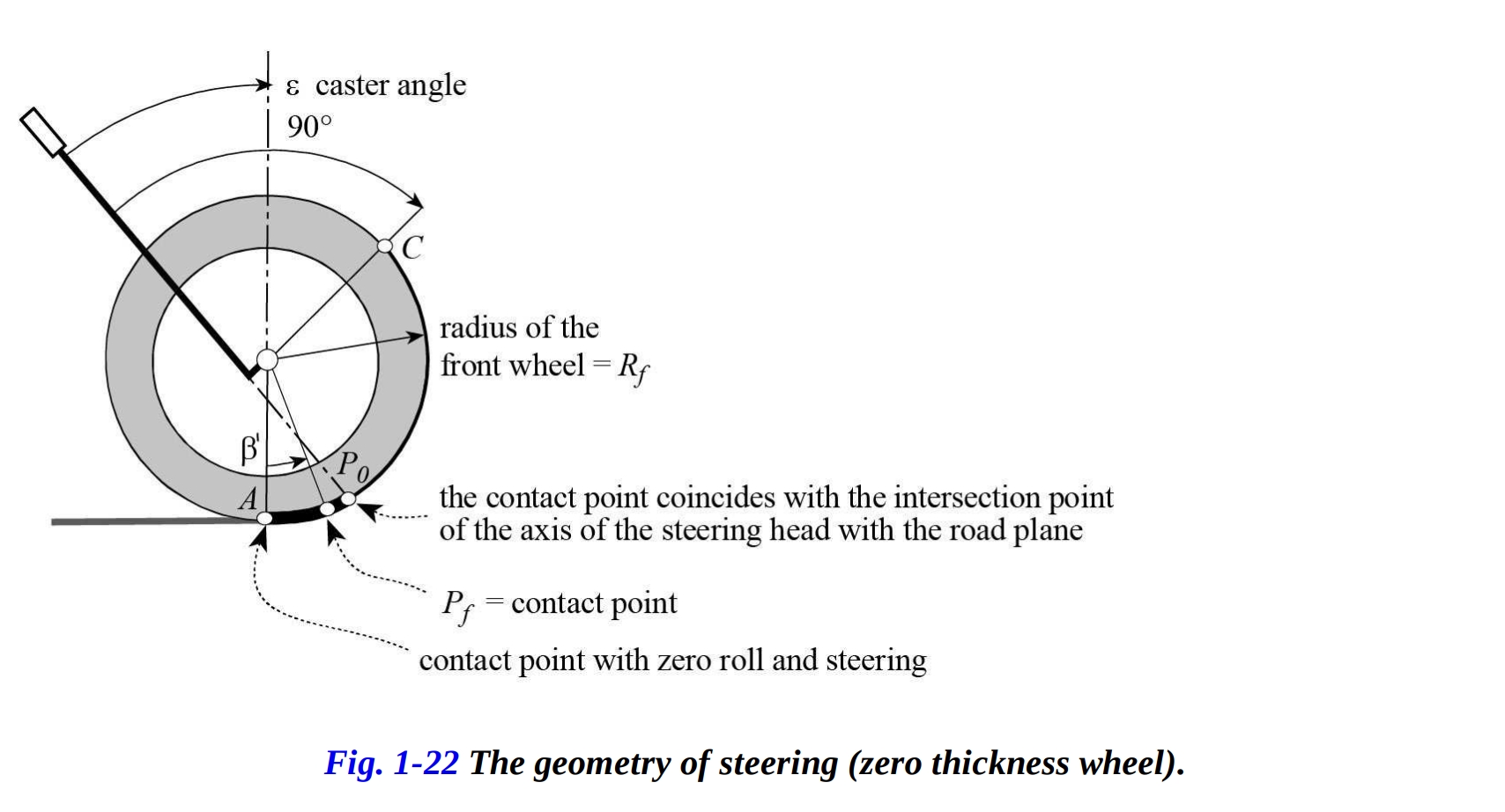
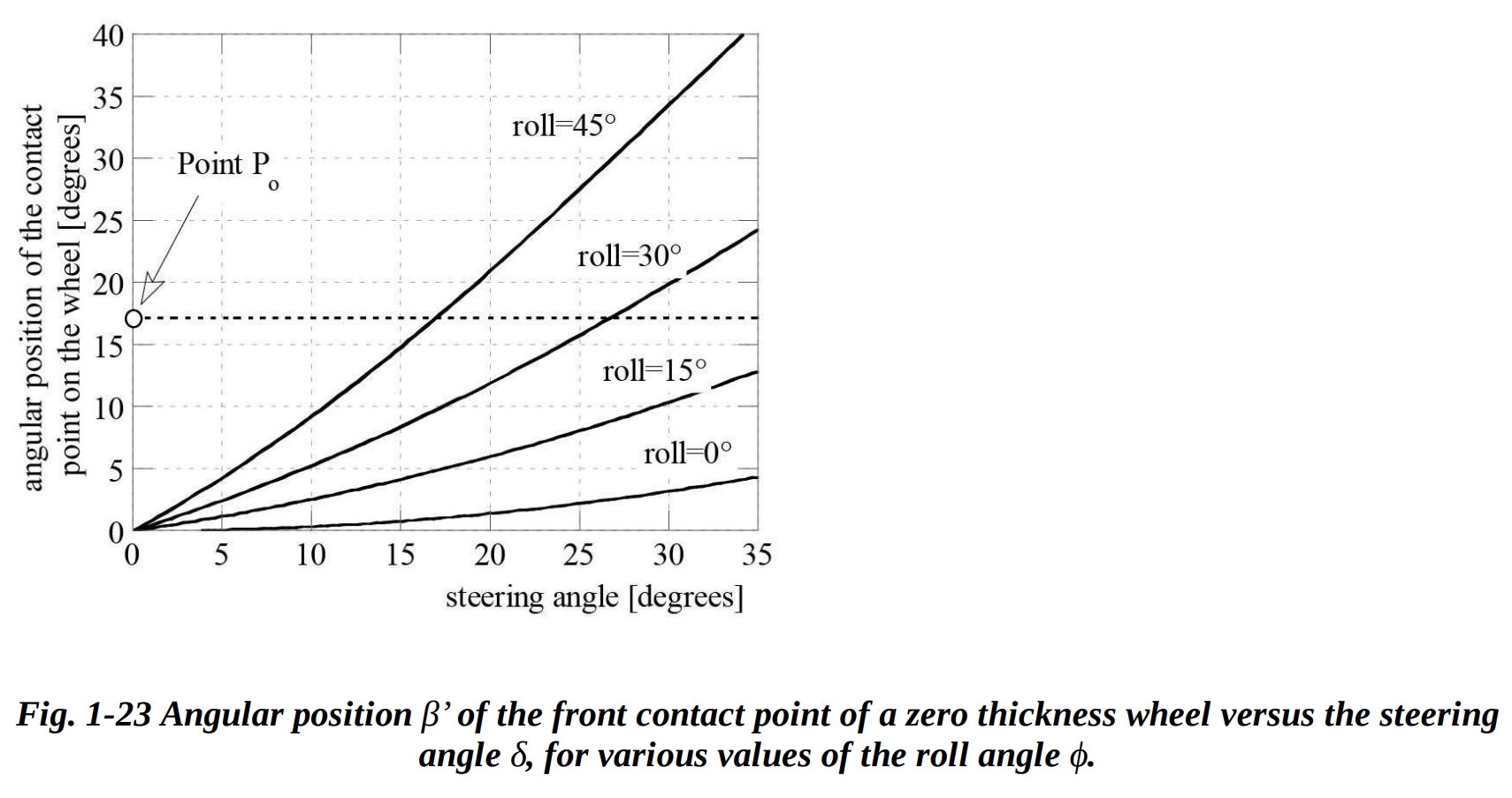
明らかに、通常の運転で使用されるロール角とステアリング角では、フロントコンタクトポイントはポイント $C$ に到達しません。実際、接点 $P_f$ は $AP_o$ の弧内を移動します。ここで、$P_o$ はステアリング軸と車輪のプロファイルとの交点です。

フロントコンタクトポイント $P_f$ は、ステアリング角とロール角に応じてポイント $P_o$ に到達します。図1-22に示されているように、設定されたロール角で右方向にステアリング操作を行うと、接点 $P_f$ は弧 $AP_o$ に沿って前方に移動し、そのトレースは道路表面上で左および前方に移動します。接点が $P_o$ にちょうどあるとき、有効なトレールはゼロです。さらに、ロール角とステアリング角の増加により、接点 $P_f$ は位置 $C$ に向かって移動し、その道路面でのトレースは右に移動し、トレールは負になります。

フロントコンタクトポイントの位置を与える前述の方程式は、ステアリング角 $\delta$ の回転が小さいと仮定することで、大幅に簡略化できます（$\sin \delta \approx \delta$ ）。この場合、接点 $P_f$ の式は次のようになります。

タイヤの厚みも無視すると、これらの方程式はさらに簡略化されます。

1.7.3 接点の横方向変位がロール運動に与える影響

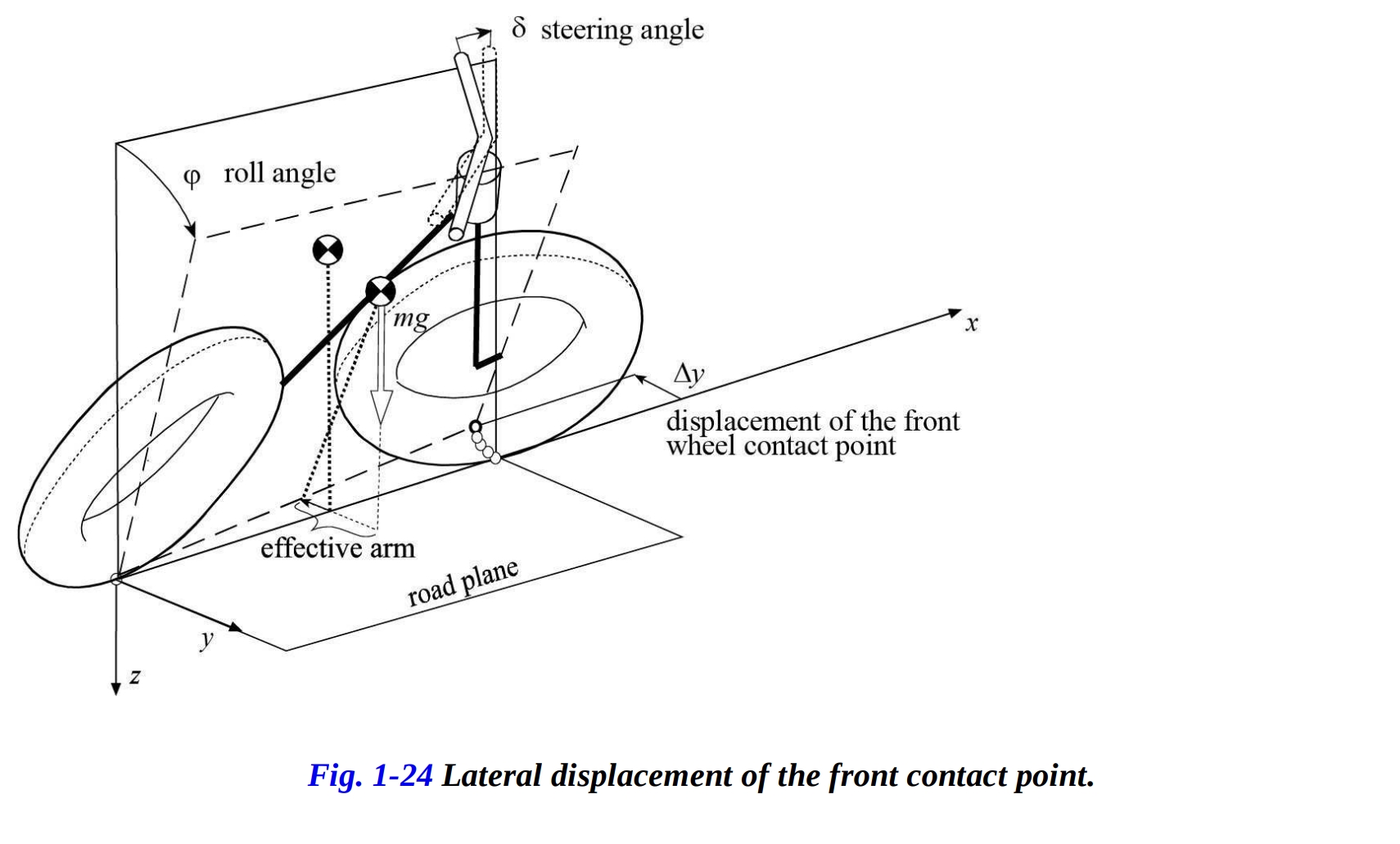
前節から明らかなように、右に操舵操作を行った場合の接点 $P_f$ の左方向への変位は、ロールを促進します。この主張は図1-24で説明されており、ここでは質量 $m$ の剛体として表されるオートバイが、ロール角 $\varphi$ が30°のカーブ上で平衡状態にある様子を示しています。

一定のロール角を維持すると仮定すると、前輪の接点 $P_f$ は操舵角 $\delta$ の増加に伴ってカーブの外側に移動します。したがって、重量モーメントは操舵角 $\delta$ の増加とともに増加します。このモーメントはオートバイをさらに傾ける傾向があります。図1-24に示すように、重量アームの増加は前輪の接点の左方向への横方向変位に比例します。横方向変位 $\Delta y$ は、特定の操舵角 $\delta$ に達すると減少し始めます。

接点は、ある特定の操舵角 $\delta$ で最大の外部変位に達します。この $\delta$ の値は、ピッチ角 $\mu$ を最小化する $\delta$ の値に対応しません。例えば、ロール角 $\varphi$ が30°の場合、最大横方向変位 $\Delta y$ は操舵角 $\delta$ が12.5°のときに発生しますが、ピッチ角 $\mu$ が最小となるのは操舵角 $\delta$ が22.5°の場合です。それぞれ図1-19および図1-14に示されています。

1.8 フロントホイールのキャンバー角

操舵角 $\delta$ がゼロ以外の場合、フロントホイールのキャンバー角 $\beta$ はリアフレームのロール角 $\varphi$ と異なります。すでに示されているように、フロントとリアのフレームのロール角は、操舵角がゼロの場合にのみ一致します。

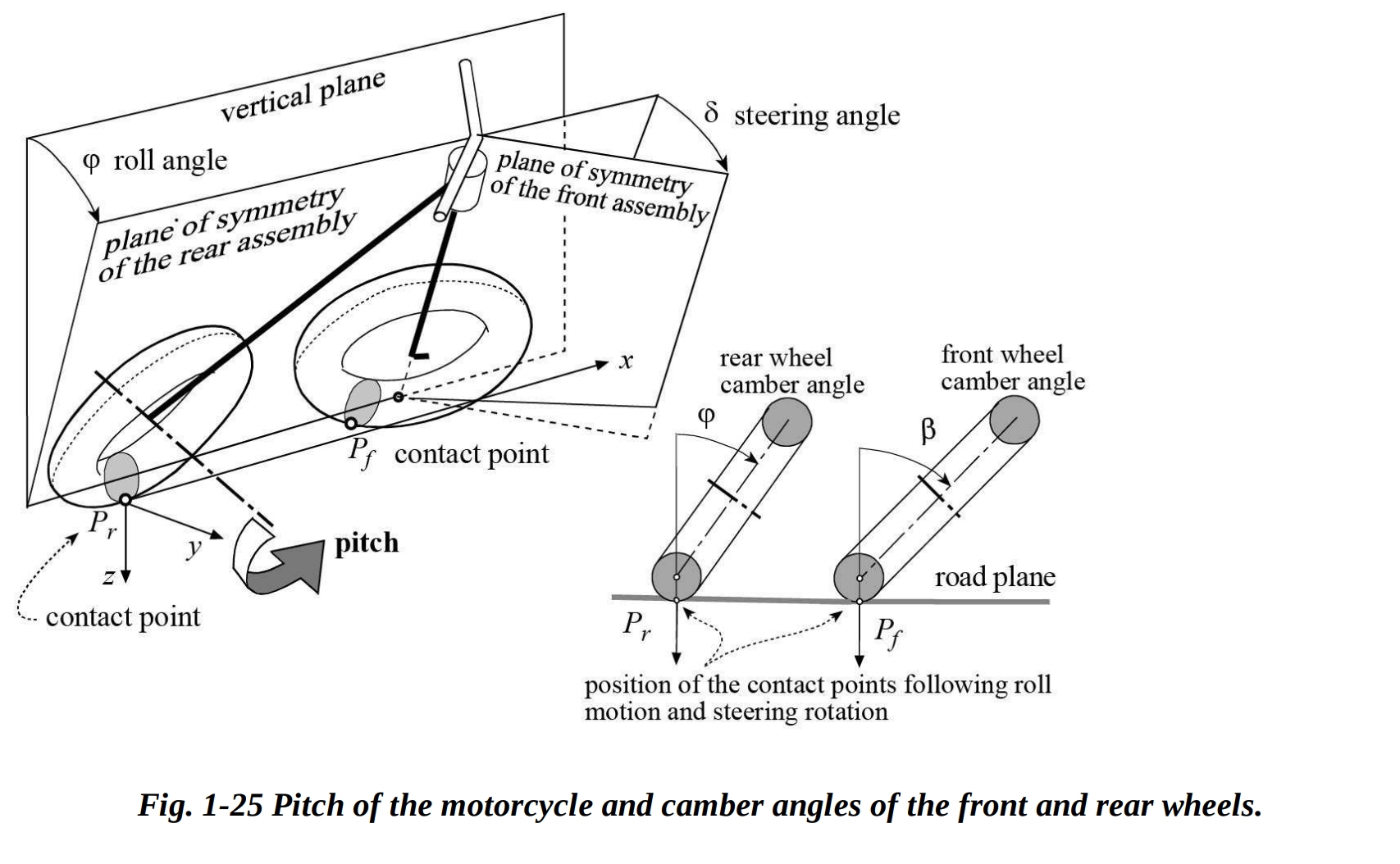
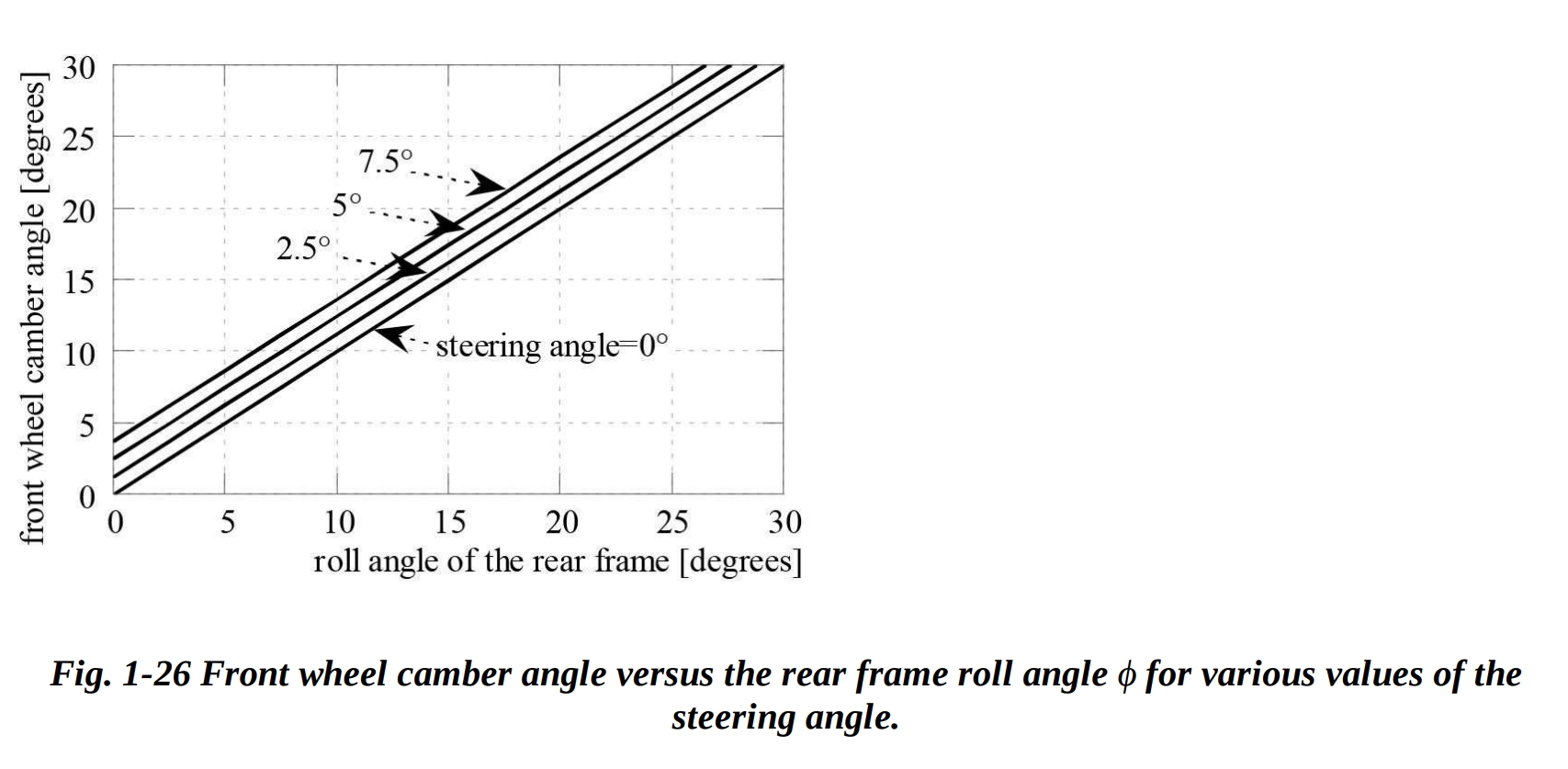
フロントホイールのキャンバー角 $\beta$ は、リアフレームのロール角 $\varphi$ 、操舵角 $\delta$ 、キャスター角 ε、およびピッチ角 $\mu$ に依存します。

操舵角がゼロ以外の場合（ロール角と同じ符号）、フロントフレームは常にリアフレームに比べてより傾いています。操舵角 $\delta$ が増加すると、キャンバー角 $\beta$ も増加します。

ピッチ $\mu$ をキャスター角 ε に対して無視すると、次のようになります：

操舵角とロール角が十分に小さい場合、フロントキャンバー角は次のように近似できます：

この式からわかるように、「同相」のロール角と操舵角、つまり、右にロール角があり、ハンドルも右に回転している場合、フロントフレームのロール角は常にリアフレームのロール角よりも大きくなります。この点は重要であり、次章で見るように、タイヤの横方向力はキャンバー角に強く依存します。

1.9 運動学的なステアリング角

運動学的なステアリング角 $\Delta$ は、リアフレームのロール角 $\varphi$ 、ステアリング角 $\delta$ 、キャスタ角 ε、およびピッチ角 $\mu$ に依存します。

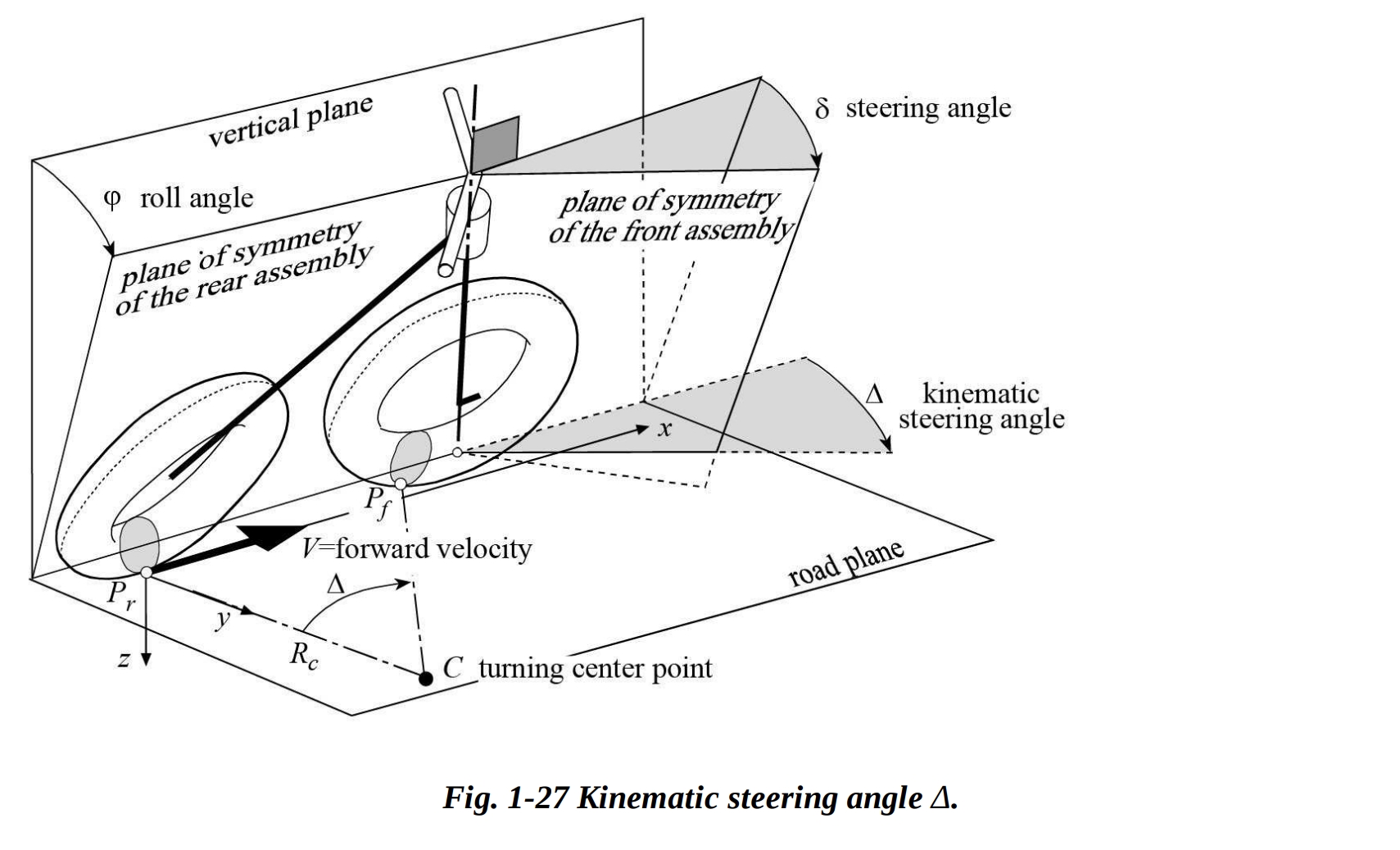
厳密に幾何学的な観点から見ると、ステアリング角 $\delta$ はリアホイール平面とフロントホイール平面の間の角度であり、運動学的ステアリング角 $\Delta$ はこの実際の角度が道路平面 $z = 0$ との交差を表します。

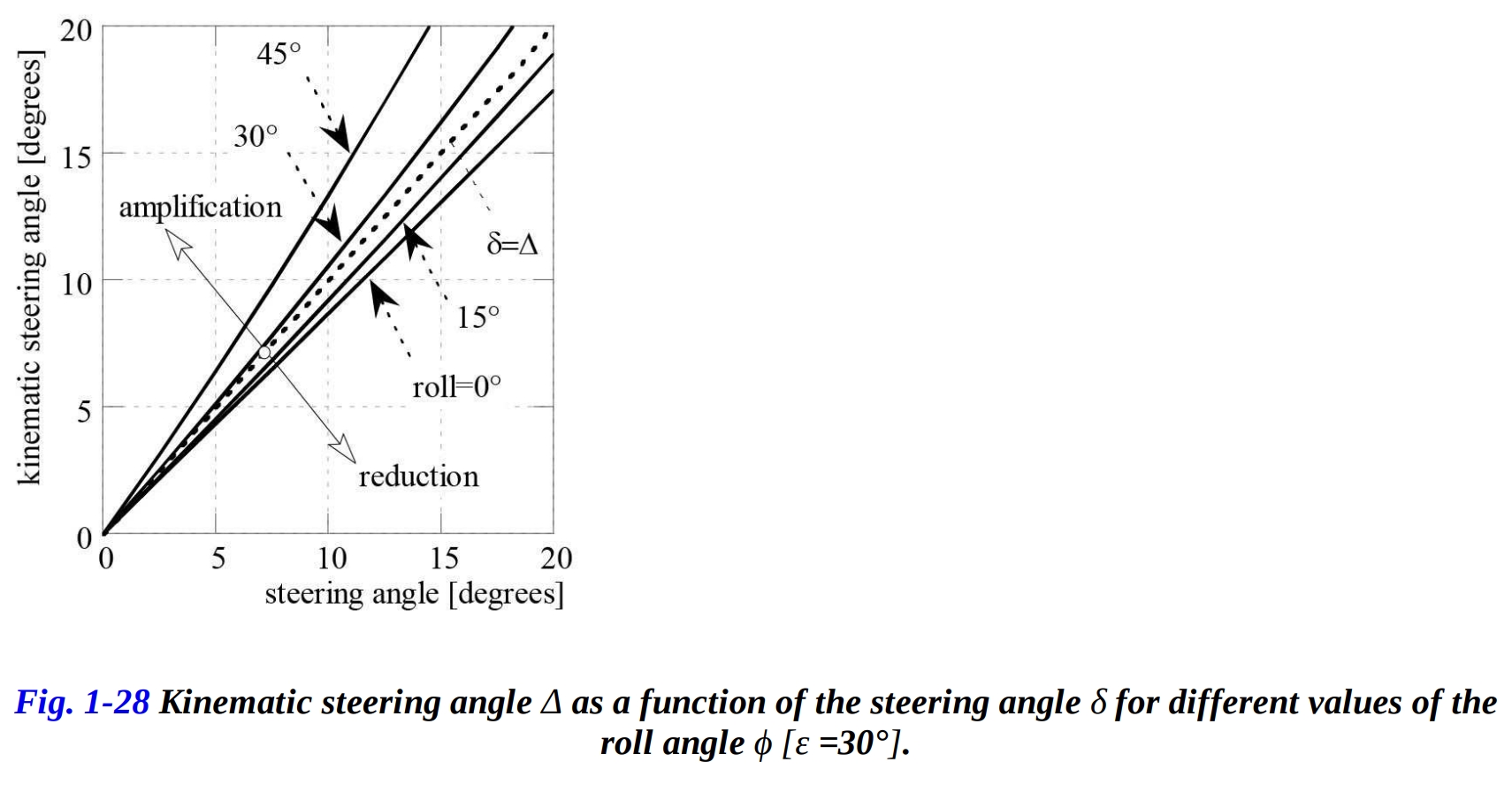
図 1-28 は、ステアリング角 $\delta$ の四つの異なる値に対する運動学的ステアリング角 $\Delta$ の変化を示しています。点線は $\Delta = \delta$ の条件を表します。したがって、運動学的ステアリング角 $\Delta$ が設定値 $\delta$ より低いままであるロール角の過渡値があり、その上では $\Delta$ が設定値 $\delta$ を上回ることが明らかです。

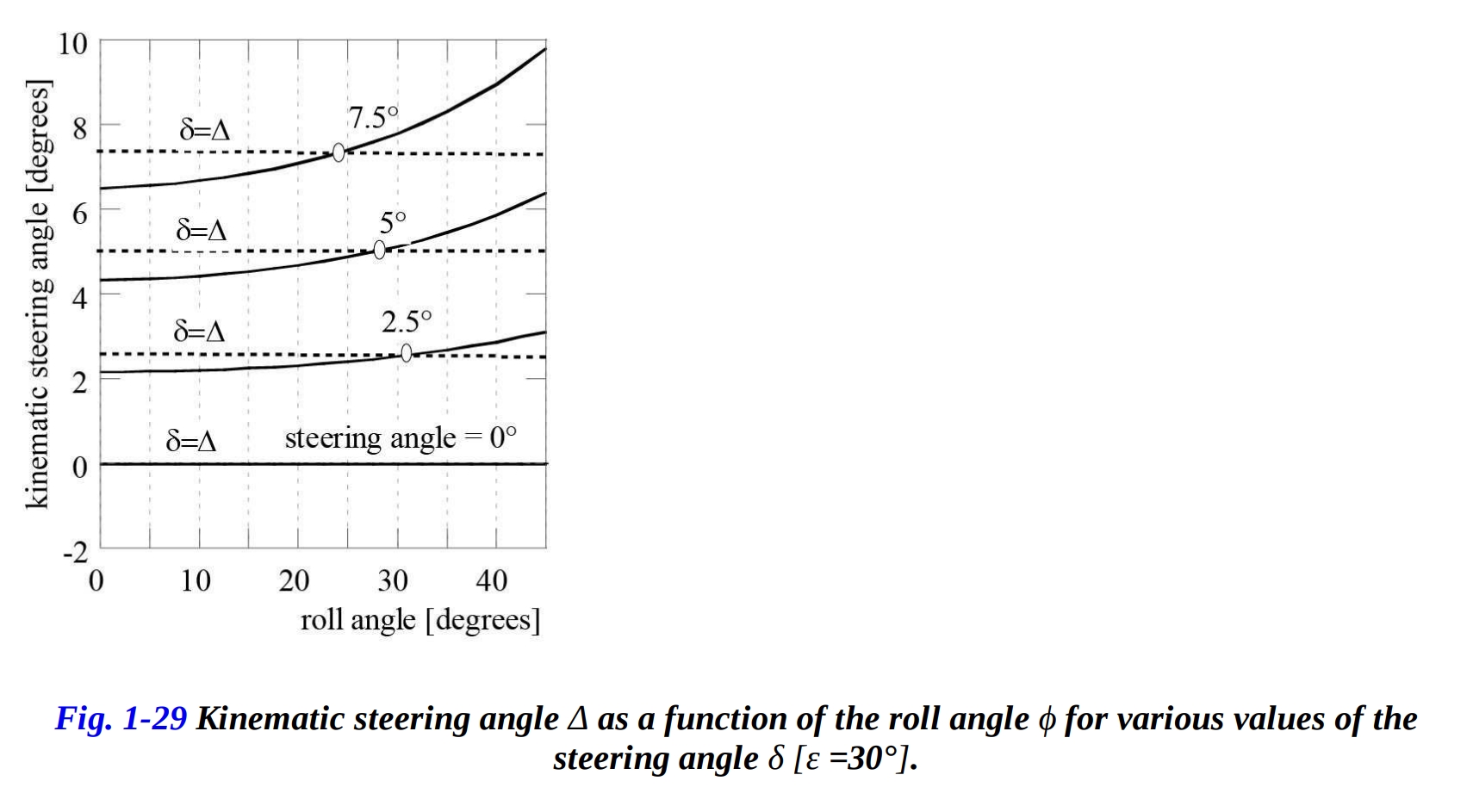
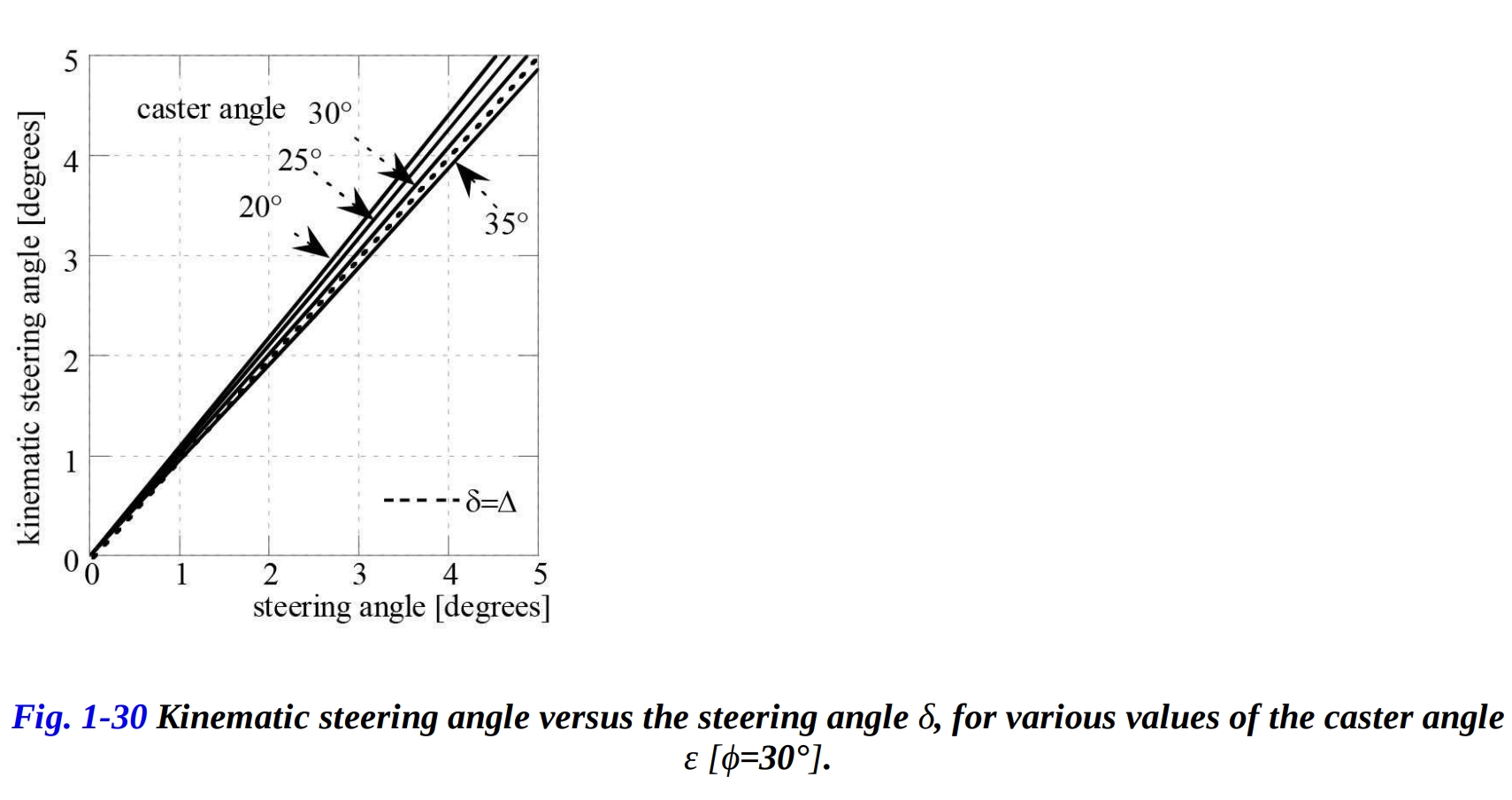
具体的には、検討された特定のケースでは、過渡値はおよそ 27.5° です。図 1-29 では、運動学的ステアリング角 $\Delta$ の変化を、今度はロール角 $\varphi$ の四つの典型的な値に対して示しています。水平の点線は、各設定値 $\delta$ に対する $\Delta = \delta$ の条件を表します。明らかに、ロール角 $\varphi$ の低い値（25°から30°）では、ステアリング機構が「減衰」しており（$\Delta < \delta$ ）、ハンドルの回転に対するステアリング機構がより感度が低く、バイクをより簡単に操縦することができます。乗り手は、幅広いハンドルバーが使用されていなくても、同じ操縦の容易さを体験します。一方、ロール角 $\varphi$ の高い値では、ステアリング機構が「増幅」され（$\Delta > \delta$ ）、方向転換に対してバイクがより敏感になります。運動学的ステアリング角 $\Delta$ は、ステアリング機構の幾何学にも依存します。図 1-30 は、ロール角が $\varphi = 30°$ に設定されています。点線は 条件 $\Delta = \delta$ を表し、キャスタ角を減少させるとステアリング機構がより感度が高くなります（$\Delta > \delta$ ）。この感度は、通常トレールの値にほとんど依存しません。実際、バイクが非常に迅速な操舵に敏感であるためには、小さなキャスタ角が必要であり、高いキャスタ角ではより操舵しやすくなります。

仮にピッチ $\mu$ をキャスター角 ε に対して無視し、$\sin \varphi \sin \delta \sin ε$ を $\cos \varphi \cos \delta$ で割ると、運動学的ステアリング角の近似式は次のようになります：

この式は、単純な幾何学的考察に基づいても得られます。 垂直な姿勢のバイクを考え、ハンドルが回転し、フロントホイールの接触点 $P_f$ が固定されているとします。

リア接触点 $P_r$ はわずかに後方に移動し、ステアリングヘッド軸の道路面との交点が横方向に移動します。この軌跡は、おおよそ円を描きます。これは、図1-31で示されています。 リアフレームの回転角 $\delta_p$ は、次の式に示すように、ステアリング角 $\delta_n$ に依存します：

ステアリング角 $\delta$ （定義上はステアリングヘッド軸に直交する平面で測定される）は、角度 $\delta_n$ （バイクの平面に直交する平面で測定される）と関係しており、次の式によって表されます（また、セクション1.4も参照）：

回転が小さいと仮定すると、次の単純化された式が得られます：

したがって、ロール角を 0 に維持したままの、前輪の接地点からのリア平面の変位は次のとおりです：

変位 $y_{P_f}$ はトレールの値に比例し、キャスター角の増加とともに減少することが、以前に24ページで示されています。

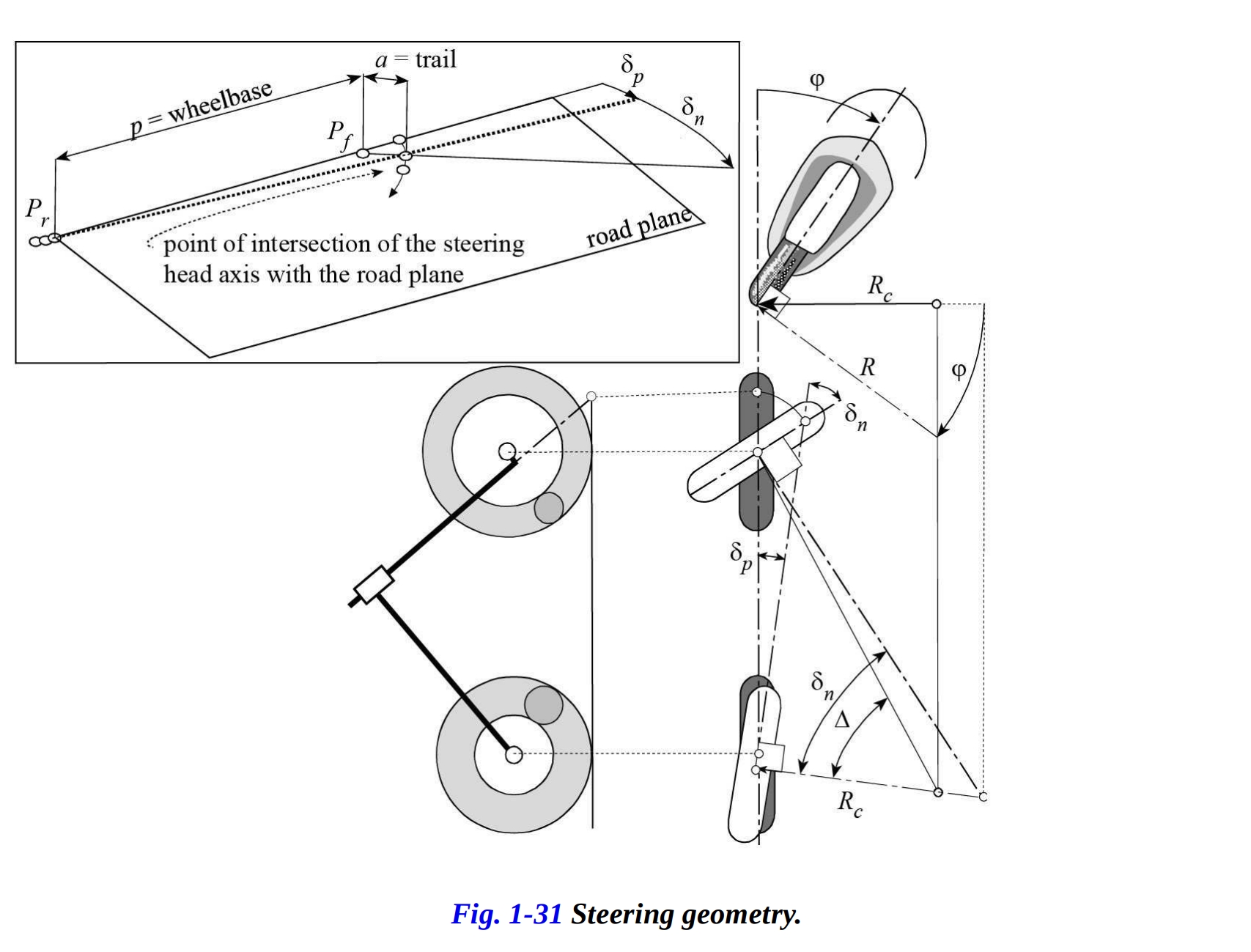
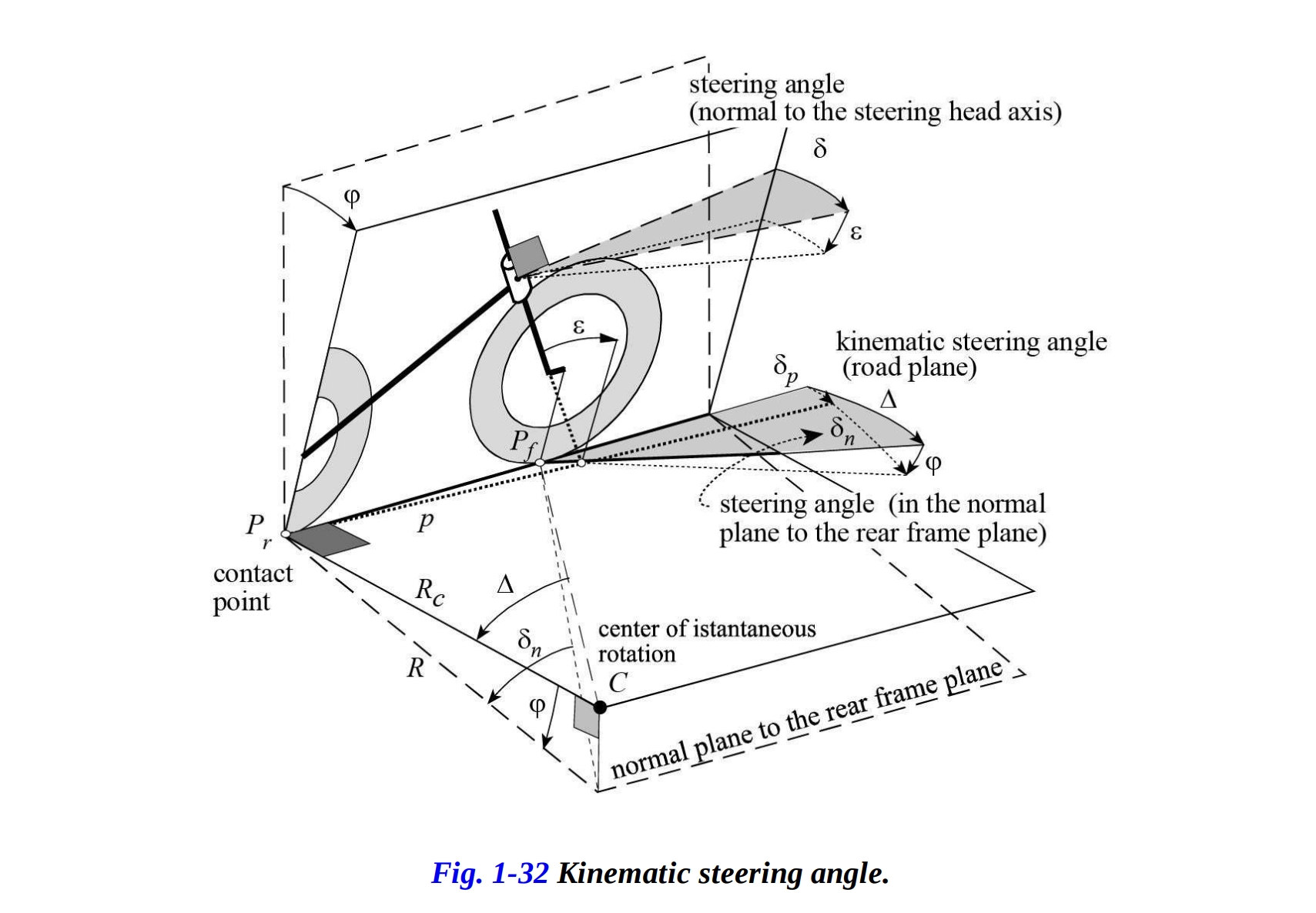
ステアリング角 $\delta$ が固定されたので、図1-31や1-32のように、一定のロール角度 $\varphi$ でバイクを傾けてみましょう。運動方向の前輪と後輪の方向によって形成される角度によって、運動学的ステアリング角 $\Delta$ が表されます。この角度の近似式は、ホイールベースと曲率半径の比率によって与えられます：

ステアリング角 $\delta_n$ は、リアフレーム平面に垂直な平面で測定されます。

運動学ステアリング角 $\Delta$ は、ロール角 $\varphi$ 、キャスター角 ε、およびステアリング角 $\delta$ の関数として、次のように表されます。

これは以前に28ページで示されました。

この式に基づいて、次のような結論を導くことができます。

• ロール角 $\varphi$ がキャスター角 ε に等しい場合にのみ、運動学ステアリング角 $\Delta$ がハンドルバーの回転角 $\delta$ と等しくなります。
• 低いロール角の場合、減衰 $\Delta < \delta$ が発生し、大きなロール角では増幅 $\Delta > \delta$ が発生します。
• キャスター角 ε の値が高い場合（チョッパーのように）、同じ運動学ステアリング角を生成するためにはより大きなハンドルバーの回転が必要です。

1.10 パス曲率

オートバイが描く経路の運動学的研究は、車輪と路面の間に横滑りがないと仮定して行われます（“運動学的ステアリング”）。 パスの曲率 $C$ （パス半径の逆数）は、前接触点 $P_f$ の位置と運動学ステアリング角 $\Delta$ に依存します。

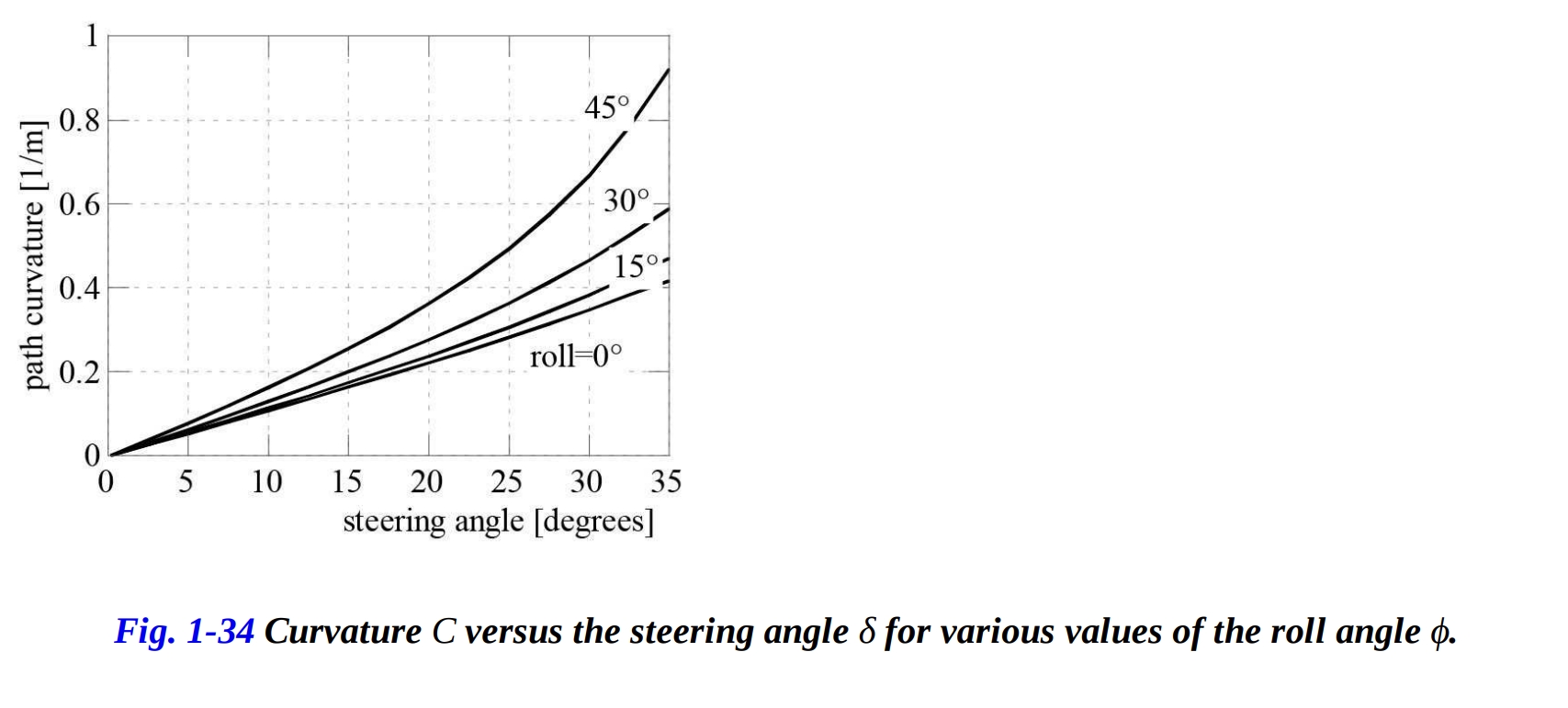
小さなステアリング角（$\sin \delta \approx \delta$ ）の場合、曲率Cはロール角 $\varphi$ とステアリング角 $\delta$ の関数として表すことができます。

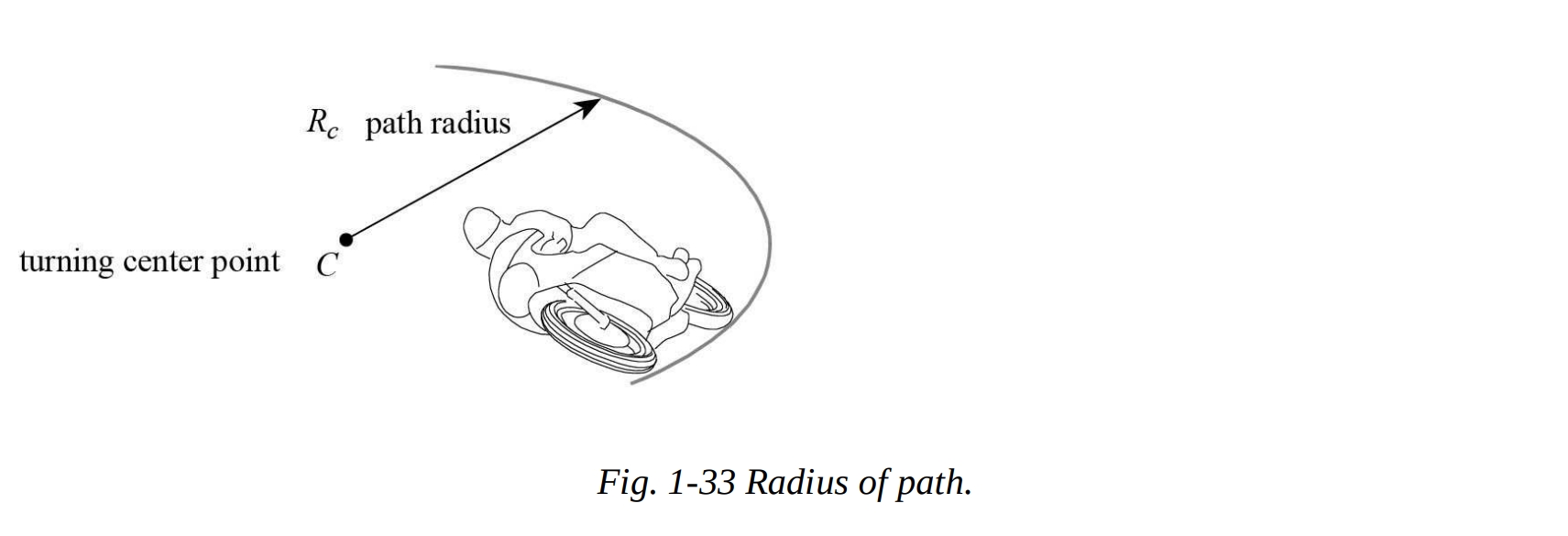
前輪の接点 $P_f$ の変位がホイールベースに比べて小さいため、曲率は次の単純化された式で計算できます。

経路の半径がホイールベースに直接比例することが観察されます。図1-34は、曲率 $C$ がさまざまなロール角 $\varphi$ の値に対してステアリング角 $\delta$ でどのように変化するかを示しています。近似式を使用した場合の最大誤差は約2%です。

1.11 曲線上の有効トレイル

トレイルは、前輪の接触点とステアリングヘッド軸が道路面で交差する点との距離です。一方、法線トレイルは、前輪の接触点とステアリングヘッド軸との垂直距離です（図1-35）。

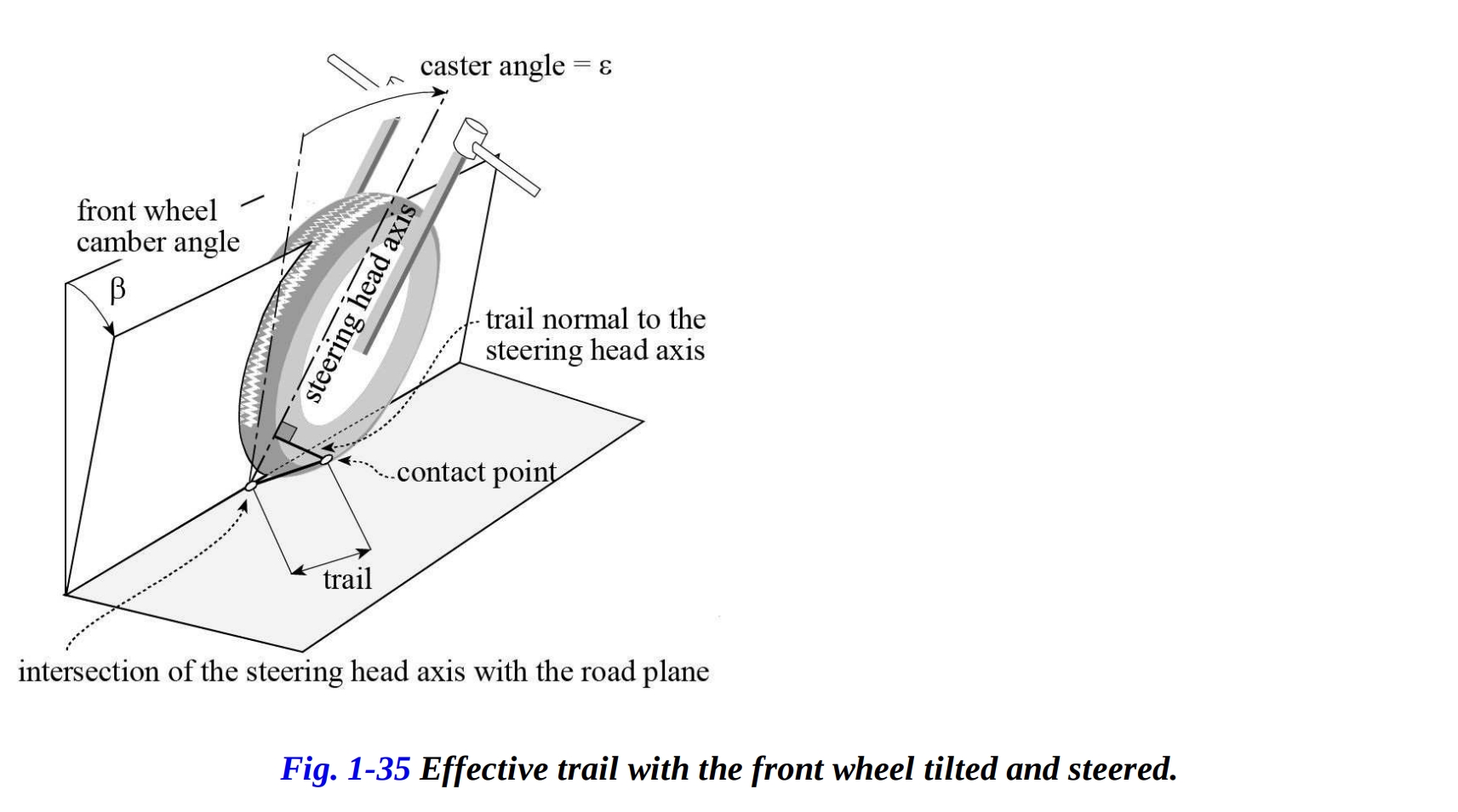
コーナリング中、法線トレイルとメカニカルトレイルは、車軸距離、キャスター角、フロントホイールのオフセット、タイヤの幾何学的特性、前輪の接触点の位置、ピッチ角に依存します。コーナリング中のの法線トレイルは、

コーナリング中のメカニカルトレイル $a^*$ は:

トレイルが、ピッチ角と前輪の接触点の位置が $\rho_f$ と $t_f$ に依存するため、フロントタイヤのジオメトリに依存することは注目に値します。 法線トレイルの重要性は、タイヤの反力（鉛直荷重と横力）によって生成されるステアリング軸周りに発生するモーメントが、法線トレイルの値に比例するためです。

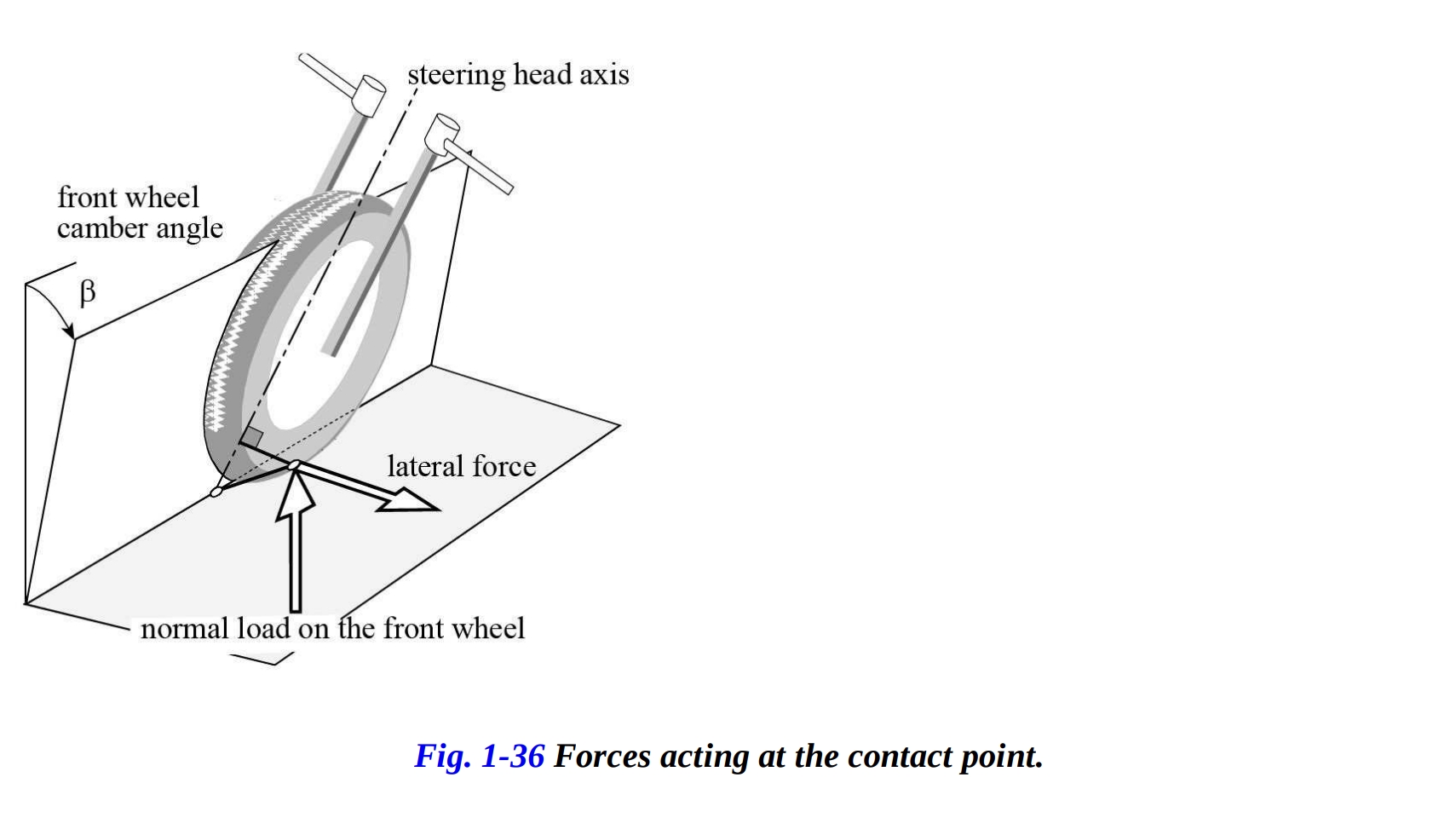
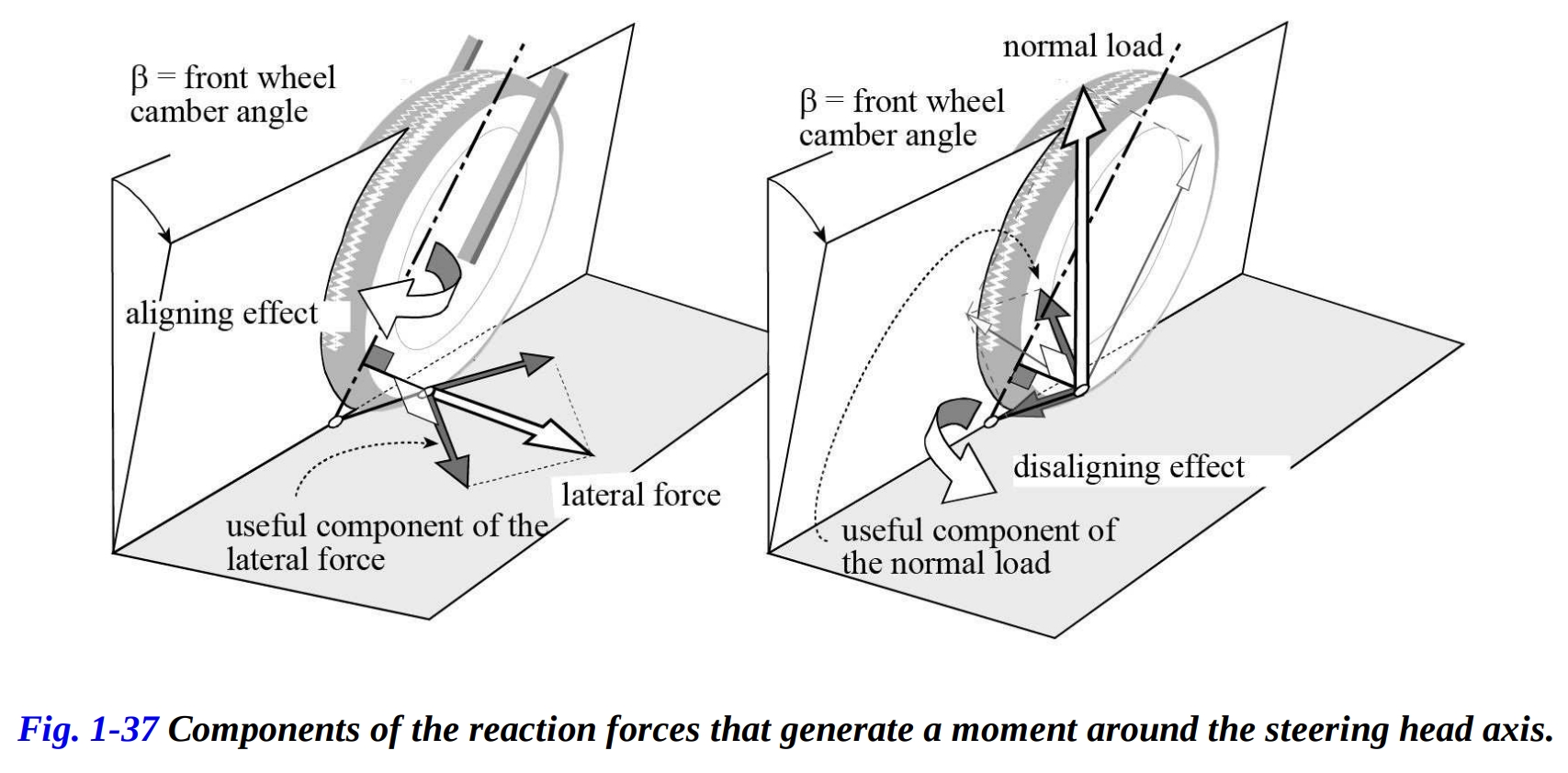
前輪の接地点での横力と法線荷重を考えましょう（図1-36）。各力は、ステアリング軸と法線トレイルに垂直に作用する成分と、ステアリング軸に平行または交差する成分に分割できます（したがって、軸周りのモーメントを生成する位置にあります。 図1-36, 37）。 法線トレイルは、有用成分の腕を表します。横力の有用成分は、車輪を進行方向の速度に向かわせますが、垂直荷重の有用成分は、車輪を曲線の内側に回転させる傾向があります。これらの有用成分によって生成されるステアリングヘッド周りのモーメントは、前部の平衡（ステアリングヘッド軸周り）に重要です。ライダーが平衡を保つために必要なトルクは、これらに依存するのです。

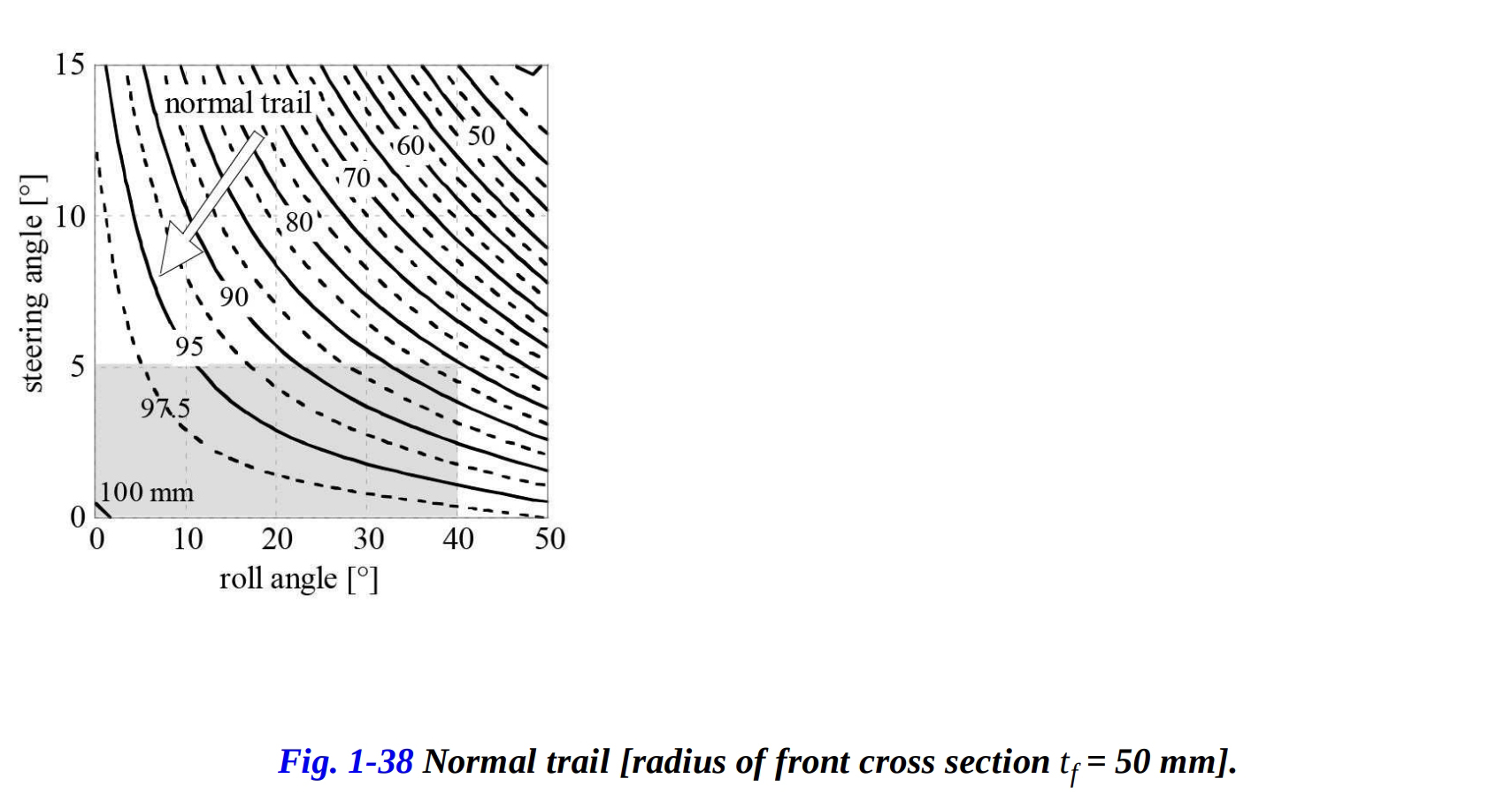
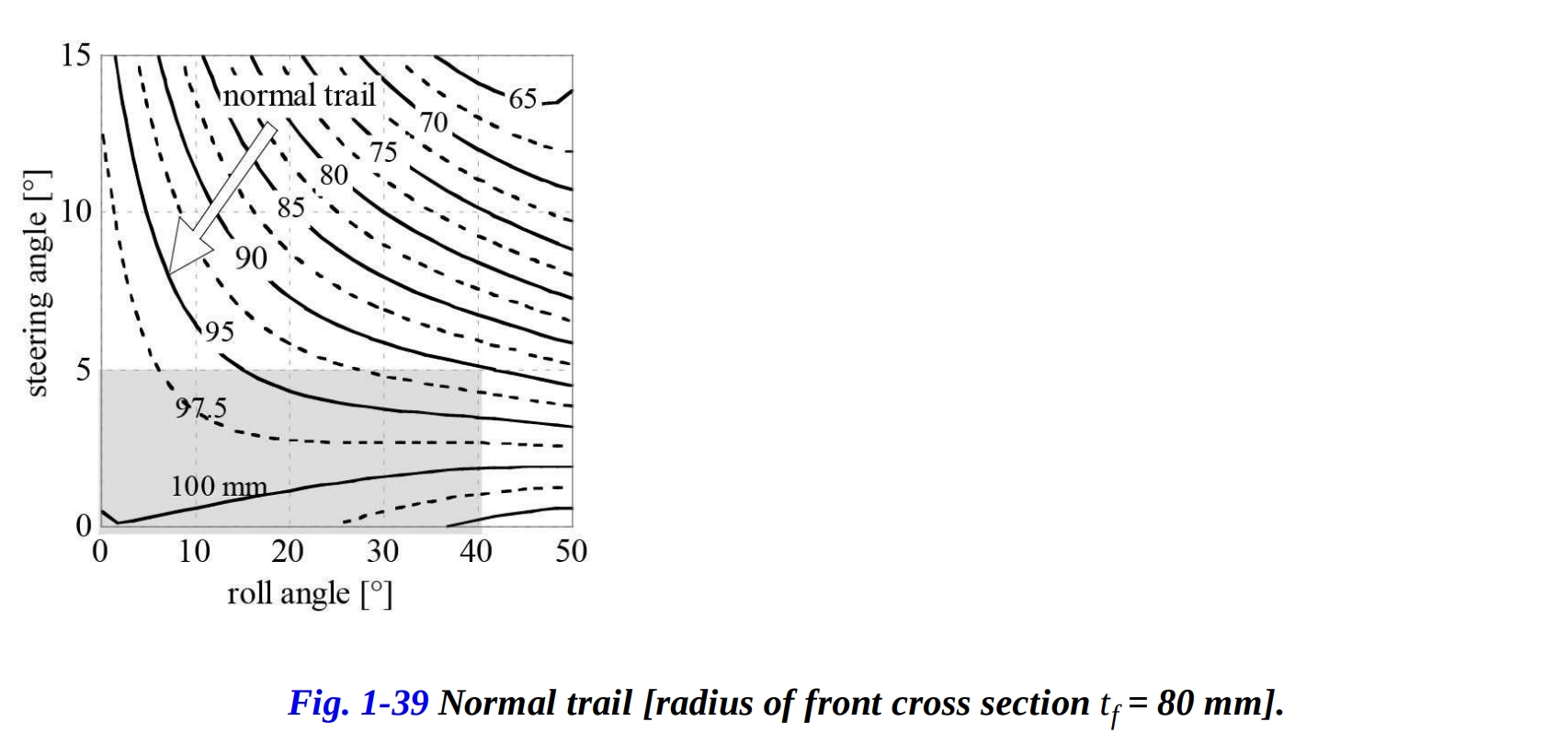
バイクがコーナリング中、法線トレイルがどのように変化するかを考察してみましょう。図1-38は、ロール角とステアリング角の関数としての法線トレイルを示しています。ロール角が増加すると、法線トレイルが減少し、特にステアリング角が増加するとさらに減少することがわかります。ただし、ステアリング角が5°未満、ロール角が40°未満の場合、トレイルの変化は20%未満にとどまります。

図1-39では、前輪タイヤ断面の半径を50mmから80mmに増やすと、これらの変動がさらに減少することが示されています。ステアリング角が5°でロール角が40°の場合、トレイルの減少率は20%から10%になります。

前輪タイヤの種類を変更すると、断面半径が変化し、したがって、コーナリング中の法線トレイル、つまり反応力の各成分が変化します。ライダーはハンドルバーにかかるトルクを通じて前部の挙動を「感じる」ため、断面半径の変化が異なる感覚を生むことは明らかです。キャスター角を変更すると、非常に類似したグラフが得られます。ただし、キャスター角の値は法線トレイルの変化にはあまり影響しません。

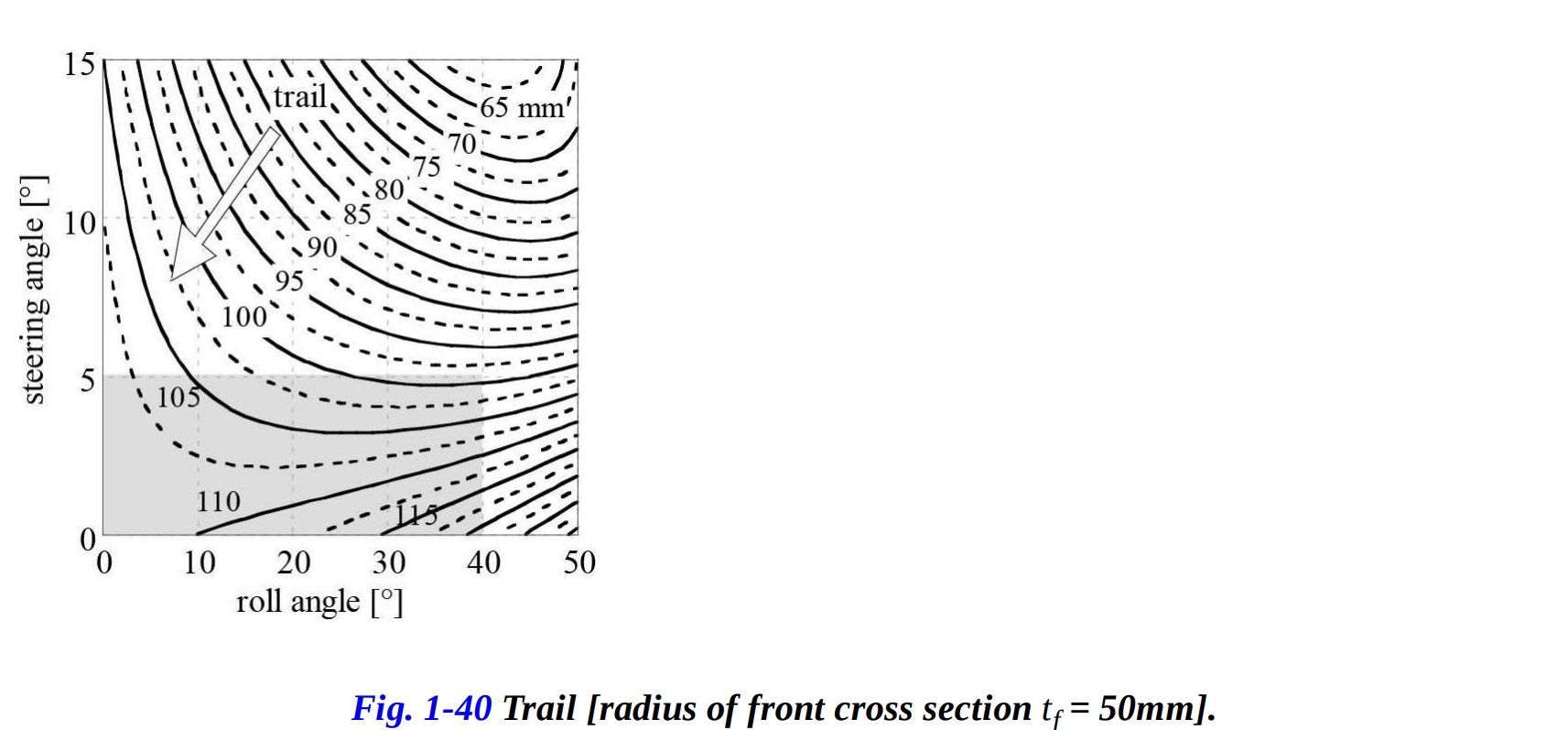
結論として、異なるバイクを比較する際には、法線トレイルが重要です。なぜなら、それには明確な物理的意味があるからです。図1-40と図1-41では、トレイルがロール角とステアリング角の関数として示されています。ロール角が増加すると、ステアリング角が小さい場合にトレイルが増加することが観察されます。これは、正規トレイルで起こることとは異なります。

まとめると、次のように言えます：

• ステアリング角 $\delta$ の増加とともに、トレイルと正規トレイルの両方が減少します。
• トレイルの値（法線トレイルまたは路面で測定されたもの）は、ロール角 $\varphi$ にも依存します。
• ステアリング角 $\delta$ の増加に伴うトレイルの減少は、フロントタイヤの断面半径と外周の半径を増やすと緩和されます。

1.12 タイヤサイズが後輪フレームのヨーに与える影響

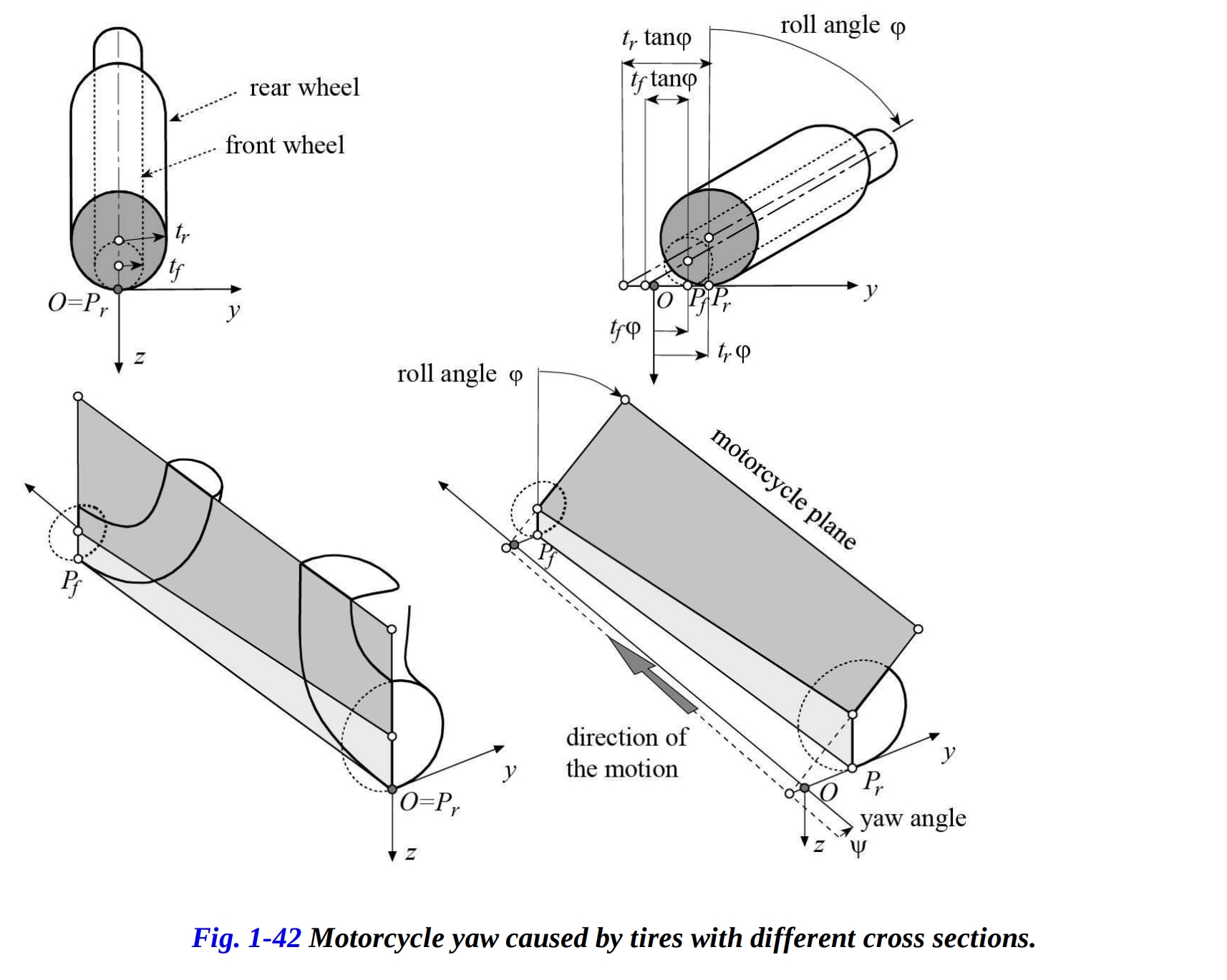
今度は、バイクが傾くときに生じるもう1つの特定の側面を調べてみましょう。異なる断面サイズのタイヤによって引き起こされるヨー効果です。 最初にバーティカルな位置にあるバイクと、ステアリング角がゼロの場合を考えてみましょう（図1-42a）。既に述べたように、SAE基準系によれば、三つ組の原点は後輪接触点 $P_r$ にあり、$x$ 軸はバイクの前進方向を表します。

ステアリング角がゼロのままバイクが傾くと仮定しましょう、図1-42bに示すように。タイヤの断面の半径が同じ場合（$t_r = t_f$ ）、後フレーム平面の路面平面との交差は前進方向と一致します。 この場合、後方面はヨーせず、むしろタイヤの横方向のローリングによって横に移動します。横方向の変位、$t_r\varphi = t_f\varphi$ 、は、ロール角 $\varphi$ とタイヤ断面の半径の積に等しい。 断面の半径が異なる値を持つ場合（$t_r > t_f$ ）、また図1-42bに示されているように、ステアリング角をゼロのままにしてバイクを傾ける動作は、後方フレーム平面の回転 $\psi$ 、つまりヨー動作を生じます。その値は次の通りです：

（例 3）

以下の特性を持つバイクを考えます：ホイールベース $p = 1400 mm$ 、タイヤ断面の半径は $t_r = 100 mm$ 、$t_f = 40 mm$ です。 バイクが直線走行（垂直なバイク、$\varphi = 0$ ）から旋回（ロール角 $\varphi = 45°$ ）に変わる場合、後方フレームのヨー角を計算します。 断面の半径の差による後フレーム平面のヨー角は、$\psi = 0.53°$ です。

2 タイヤ

オートバイのタイヤは、最も重要な部品の1つです。その基本的な特性は、小さな障害物に遭遇した場合でも、車輪と道路の間の接触を維持することができる柔軟性です。 乗り心地を向上させるだけでなく、タイヤは接地性を向上させ、大きな駆動力やブレーキング力を地面に伝達するために重要であり、また横方向の力を発生させるのにも重要です。オートバイの性能は、そのタイヤの特性に大きく影響されます。その重要性を理解するためには、車両の平衡と運動の制御が、タイヤのコンタクトパッチと路面の間で作用する縦方向および横方向の力の発生によって行われることを考える必要があります。これらの力は、ライダーがステアリング機構、アクセル、およびブレーキシステムを通じて行動を起こすことによって発生します。

2.1 タイヤと路面の接触力

オートバイのダイナミックな観点から、タイヤの全体的な振る舞いを表現することは重要であり、タイヤ自体に作用する前進速度、キャンバーアングル、縦滑り、横滑り、および荷重を用いて接触の力とモーメントを表現できるモデルを通じて、さまざまな使用条件での振る舞いを描写することが求められます。

マクロな観点から見ると、タイヤと路面の相互作用は、以下のような3つの力と3つのモーメントからなるシステムで表現されます（図2-1参照）：

• 道路面と車輪面の交差する軸に沿って、接触点を通る（駆動時は正、ブレーキング時は負と仮定される）x方向の縦力；
• 路面に直交する鉛直方向の力（車輪に作用する鉛直荷重で、上向きが正と仮定される）、z軸に沿う；
• x軸周りの転倒モーメント、
• y軸周りの転がり抵抗モーメント、
• z軸周りのヨーイングモーメント。

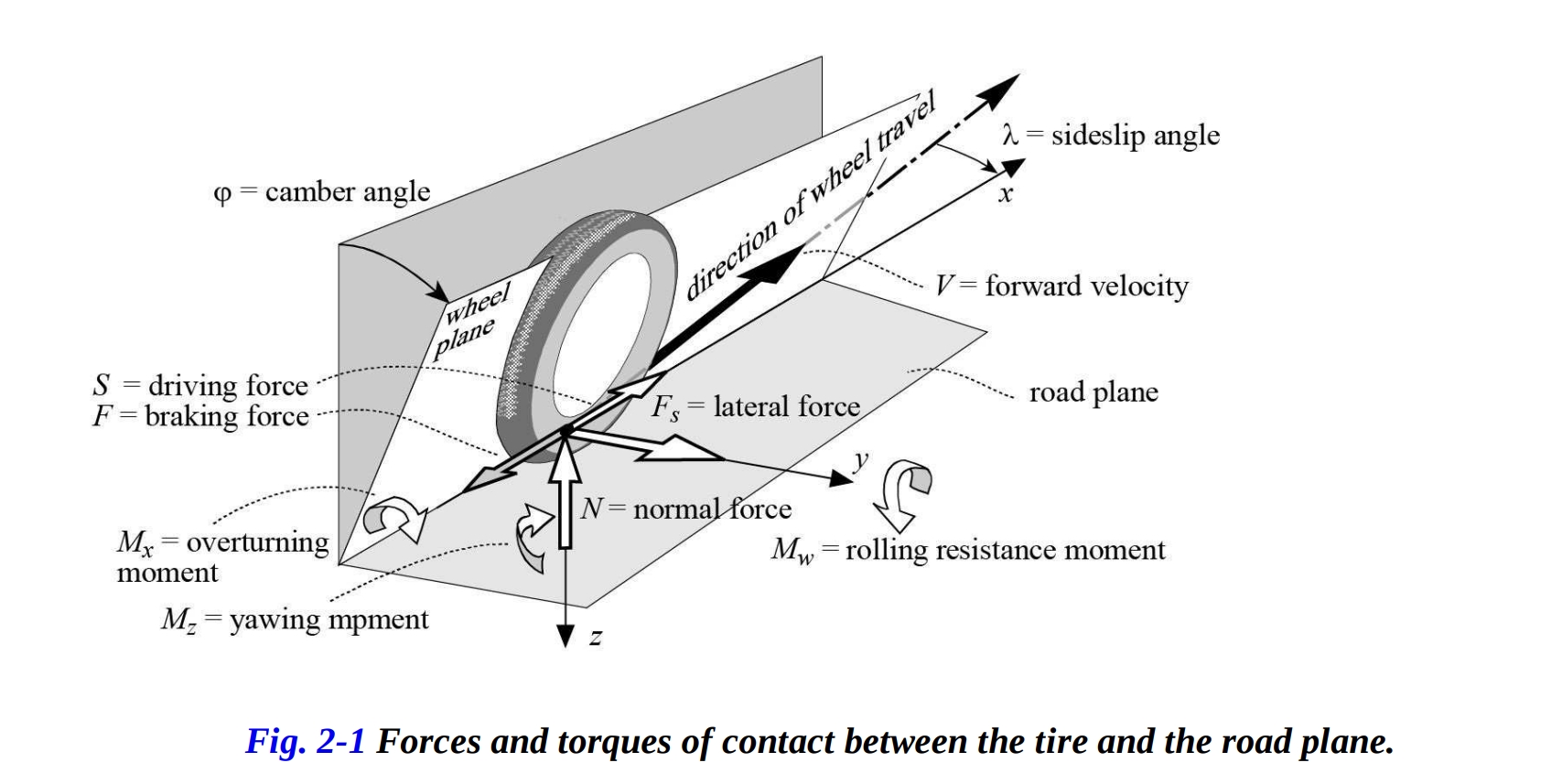
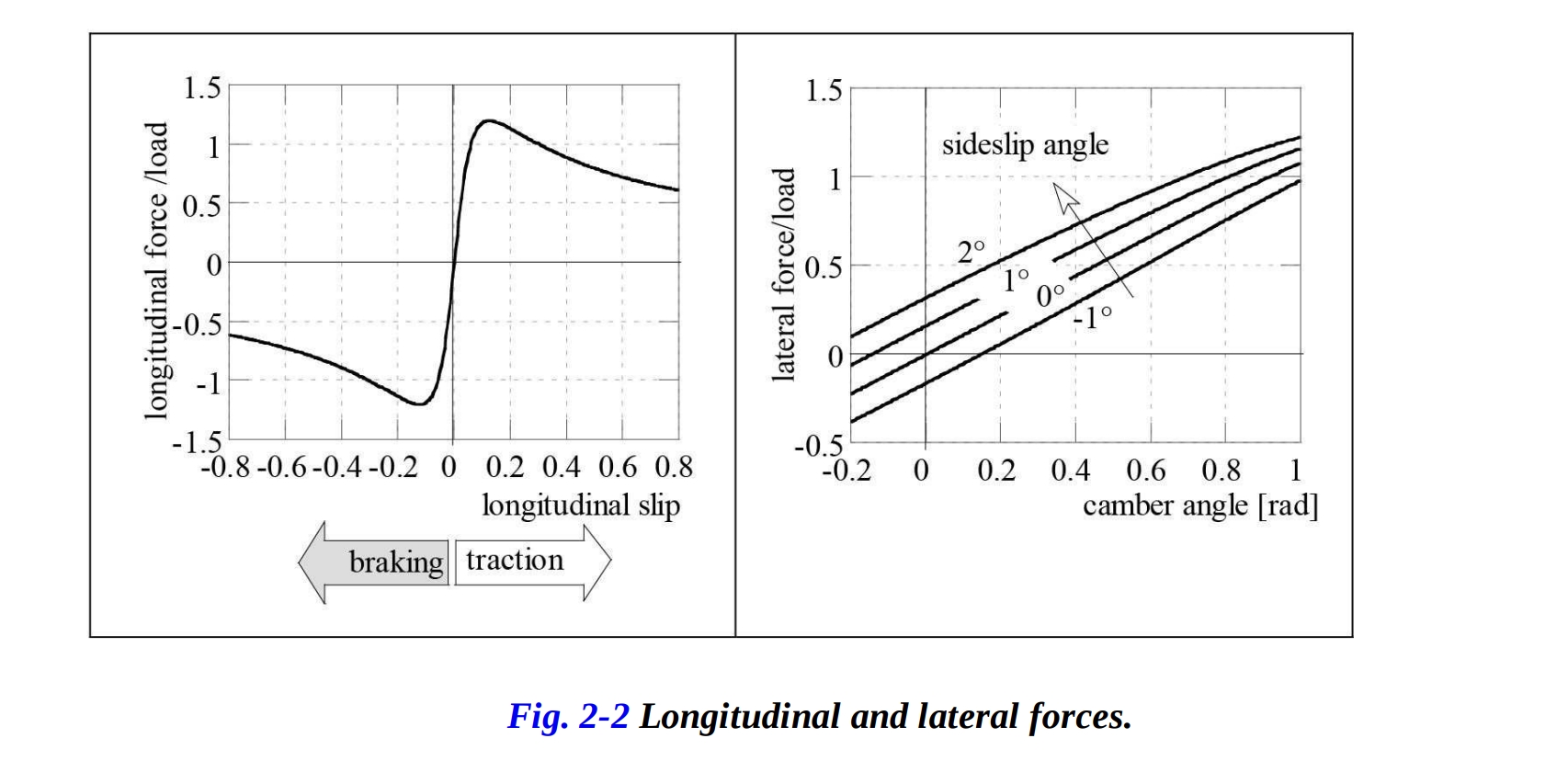
図2-2では、純粋なスリップ状態での典型的な縦方向および横方向の力が描かれています。 純粋なスリップは、縦方向または横方向のスリップが単独で発生する状況を表します。縦方向の力は縦方向のスリップに依存し、明確なピークを示しますが、横方向の力はキャンバーアングルとスライプアングルの両方に関数として表されます。図2-2に描かれているような形状を持つ曲線は、“マジックフォーミュラ”と呼ばれる数学的な式で表すことができます。

2.2 実験結果の表現のための”マジックフォーミュラ”

Ρacejka（1993年）によって提案されたモデルは広く使用されています。このアプローチは主に経験的であり、その結果はタイヤの実際の挙動を非常によく再現します。このモデル全体は、“マジックフォーミュラ”と呼ばれるもので成り立っています。これは、縦方向の駆動力またはブレーキ力、横力、または $z$ 軸周りのモーメントを表すために使用できる単一の式です。その式は次のとおりです：

ここで、$B$ 、$C$ 、$D$ 、および $E$ は4つのパラメータであり、$S_v$ は $y$ 軸に沿った曲線の平行移動を示し、$S_h$ は $x$ 軸に沿った曲線の平行移動を示します。

大きさ $y$ は、縦方向の推力または横方向の力を表すことができ、$x$ はそれに対応するスリップ量を表します。図 2-3 は、Pacejka 曲線の典型的な変化を再現し、そこに現れる 4 つのパラメータの意味を視覚的に示しています。

　・パラメータ $D$ はピーク値を表し（ただし $E < 1$ かつ $C \geqq 1$ ）、垂直荷重に依存します。

　・パラメータ $C$ はスリップが無限に近づくときに曲線がとる漸近値を制御し、この方法で曲線の形状を決定します。

　・パラメータ $B$ は原点からの曲線の勾配を決定します。

　・パラメータ $E$ はピーク付近の曲率を特徴づけ、同時にピーク自体の位置を決定します。

原点での勾配は、$BCD$ の積で与えられることが示されています。

※参考文献:“Magic Formulaについて”

2.3 ローリング抵抗

平らな表面上で滑りなく回転するホイールを考えます。ローリング半径は、前進速度を角速度で割った比率で定義されます。

自由運動中の有効なローリング半径は、図 2-4 に示されているように、タイヤの変形のため、無負荷のタイヤの半径よりも小さくなります。その値は、タイヤの種類、その径方向の剛性、荷重、空気圧、および前進速度に依存します。自由運動中のその値は、無負荷のタイヤの半径よりも小さく、しかしタイヤの中心から路面までの距離よりも大きいことが示されています。その近似値は次の式によって与えられます：

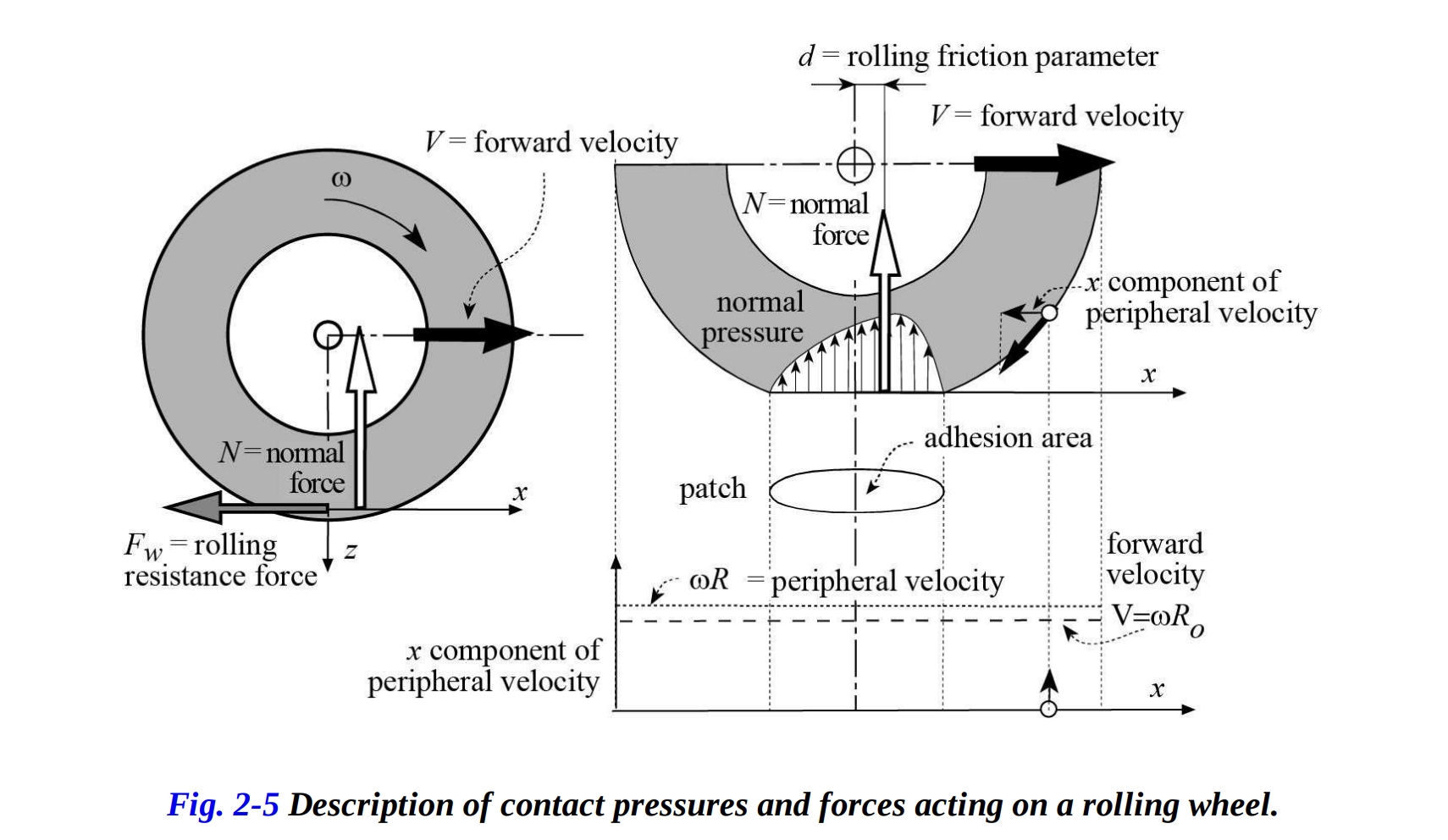
タイヤが転がる過程で、トラック上を通過する円周の部分がたわみます。接触面では、荷重による法線応力と、円周のアークとそのトレッド弦（接触トレッドの長さを表す）との長さの違いによる剪断応力が発生します。タイヤ材料のヒステリシスによる、タイヤのカーカスを変形させるために費やされたエネルギーの一部が、緩和の次の段階で回復されないか、遅れて回復されます。これにより、接触圧の分布が変化し、それが非対称になり、車輪の軸の前の領域でより高くなることがあります。

図2-5に示すように、法線接触圧の合力は、車輪の中心から距離 $d$ だけ前方にずれています。この前方へのずれを、転がり摩擦係数と呼びます。したがって、車輪を一定の前方速度で移動させるためには、次のような転がり抵抗モーメントを克服する必要があります。

転がり抵抗は、前進運動の逆方向の抵抗力を介して表現されます。その値は、転がり抵抗係数 $fw$ と鉛直荷重の積で与えられます。

タイヤの種類（ラジアルやバイアス）、寸法、特性、温度、および使用条件に加えて、転がり抵抗係数は主に前進速度と空気圧に依存します。転がり抵抗係数はキャンバー角とともに増加します。典型的な値は約0.02程度です。

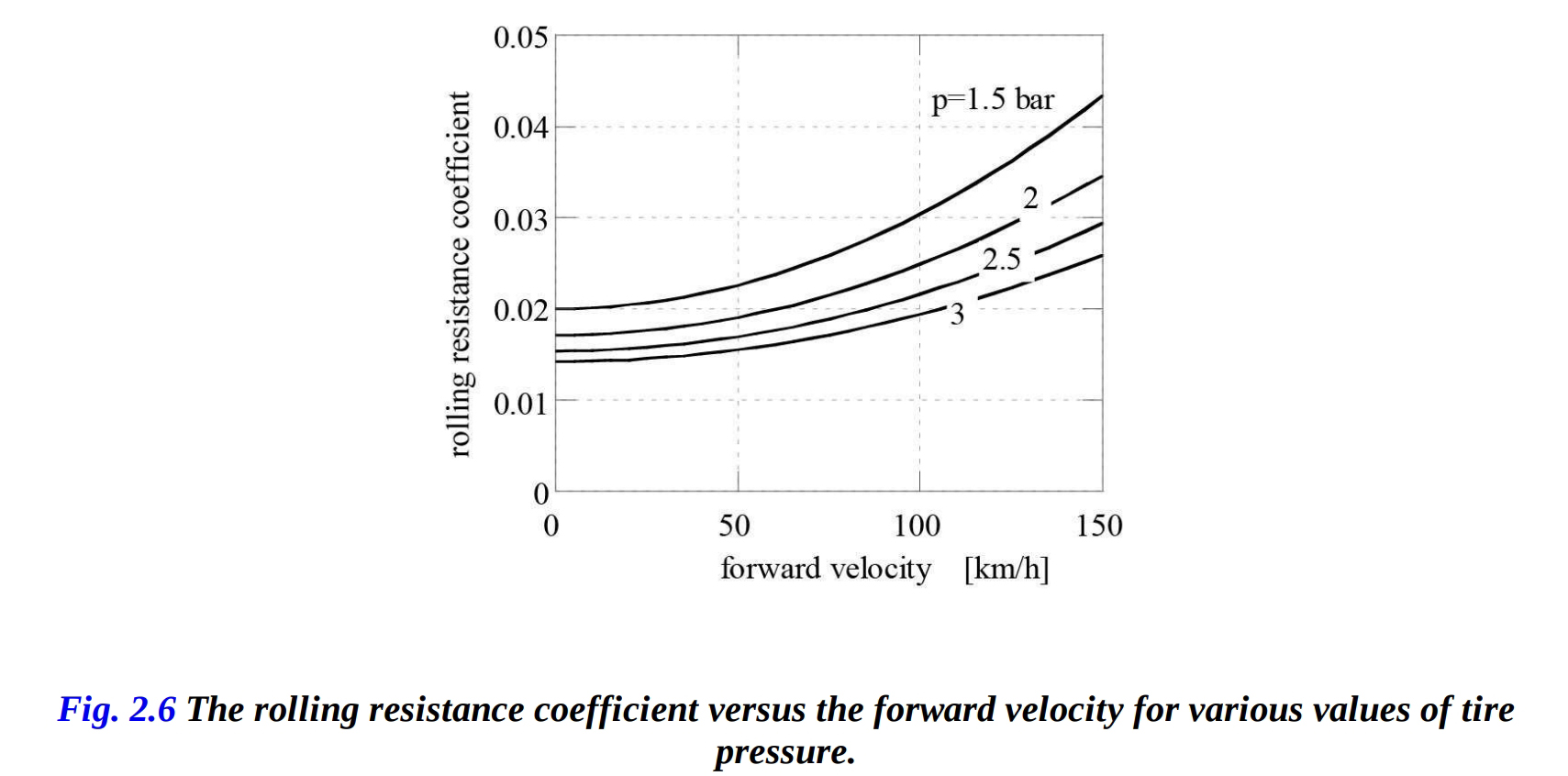
ケビン・クーパー（参照：J.ブラッドリー、1996年）は、オートバイタイヤの転がりによる抵抗に関する損失を計算するための次の経験的な式を提案しました。この式は、空気圧と前進速度を考慮に入れます。

速度は時速キロメートルで表され、タイヤの圧力 $p$ は $bar$ で表されます（$1bar$ は約$1 atm$ です）。図2-6は、一定のタイヤ圧力値での速度変化に対する転がり抵抗係数の変化を示しています。圧力の増加が転がり抵抗を減少させることが観察されます。 転がり抵抗力によって消費されるエネルギーは、抵抗力と前進速度の積で与えられます。

ここで、$N$ は車輪への荷重を表し、（ニュートンで表されます）; 消費されるエネルギー $P$ は、キロワットで表されます。 要約すると、転がり抵抗力は次の要素に依存します：

• 空気圧
• タイヤの変形（材料のヒステリシスを考慮したもの）
• タイヤと路面の相対的なすべり
• ベンチレーションによる空気抵抗

このうち、最も重要なのは最初の要因です。ベンチレーションによる損失は、車輪と循環する空気との相互作用によって引き起こされます。この相互作用は、車輪自体の形状（スポークの有無）、タイヤのプロファイル、および回転速度に依存します。

例1

質量が200 kgのバイクがあり、速度が異なる2つの場合を考えます：100 km/h および 250 km/h。タイヤの空気圧が2.25 barとして、転がり抵抗を克服するために消費されるパワーを求めます。 100 km/hの速度で転がり抵抗を克服するために消費されるパワーはわずか1.1 kWですが、250 km/hの速度ではそのパワーは12 kWに上昇します。

2.4 縦方向力（駆動・ブレーキング）

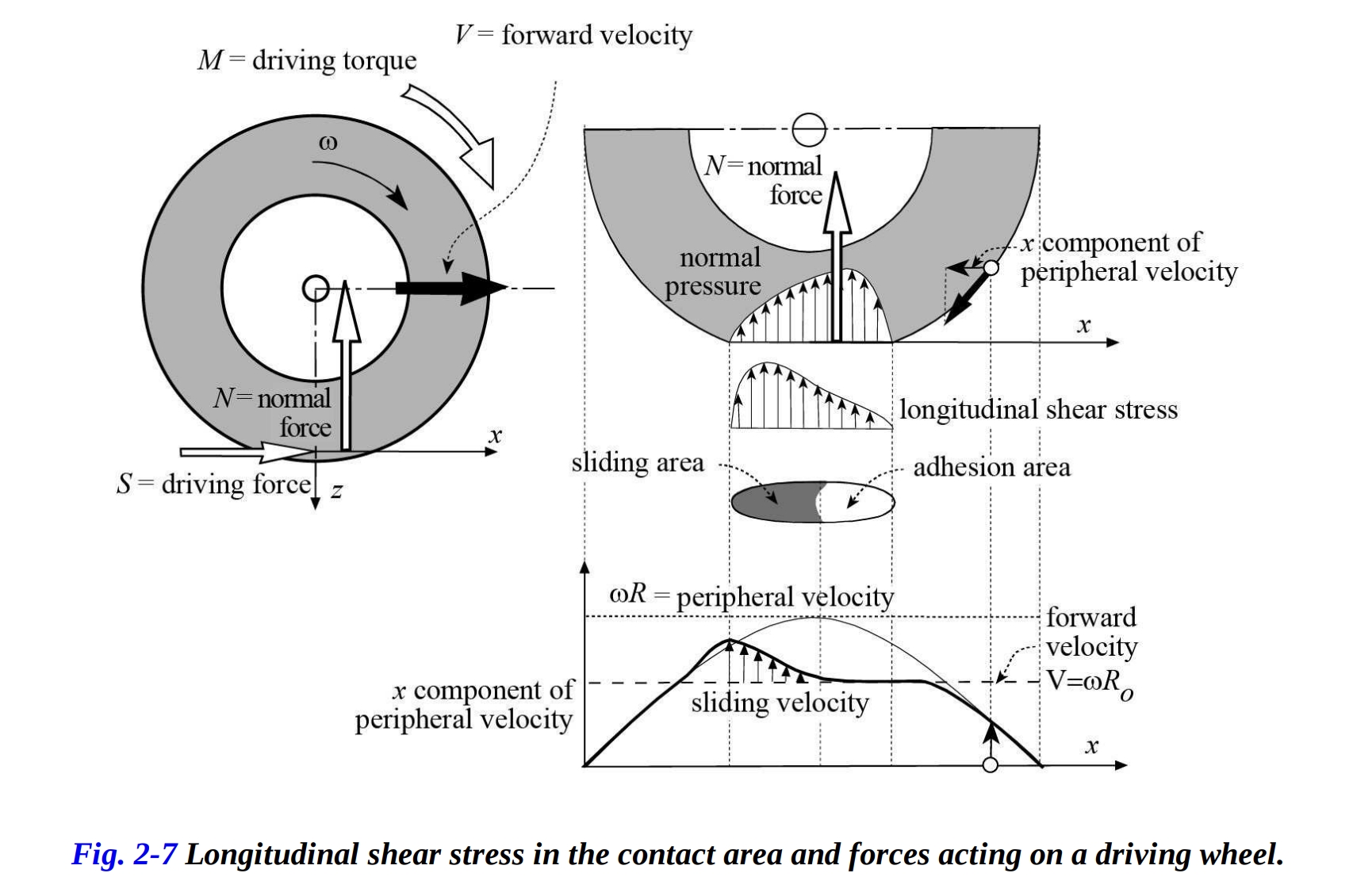
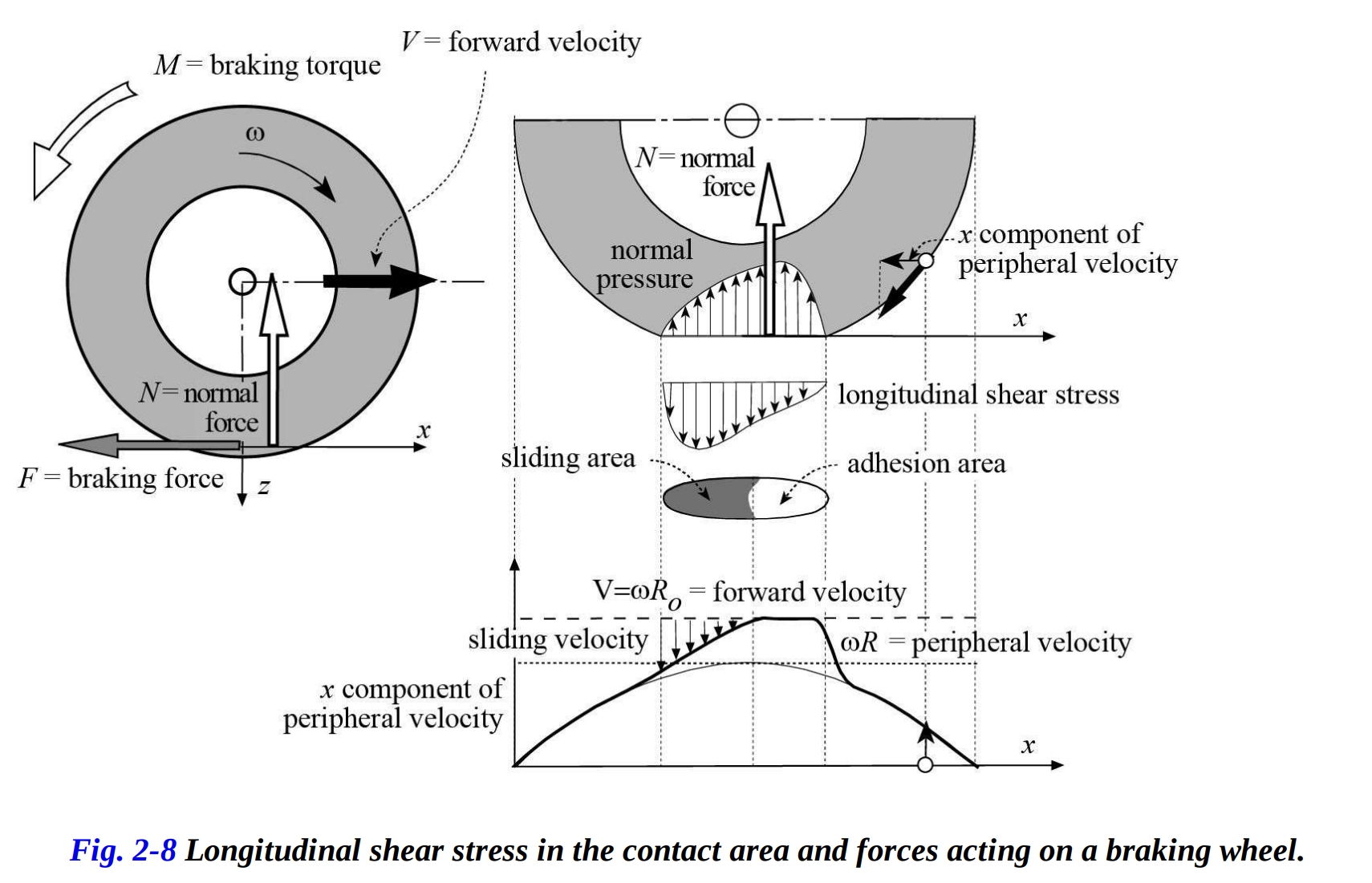
駆動またはブレーキング力の存在により、接触面に沿ったさらなる縦方向せん断応力が生成されます。駆動力の場合、周方向応力は接触面の繊維を圧縮します（図2-7）。ブレーキング力の場合、繊維は引張応力を受けます（図2-8）。

したがって、トラクションがかかる場合、接触点の前進速度はタイヤの周辺速度よりも低くなります。一方、ブレーキングの場合、接触点の前進速度はタイヤの周辺速度よりも高くなります。これは、縦方向の滑りによって表されます。滑りは、滑り速度（$V - \omega R$ ）と前進速度 $V$ の比率で定義されます。

トラクションがかかっている時、縦方向の滑りは正であり、ブレーキングの場合は負です。後者の場合、縦方向のせん断応力は前進速度の符号と逆です。 駆動輪の場合、接触領域で同じ符号の縦方向のせん断応力が生成されるため、タイヤのトレッドは接触パッチで圧縮されます。パッチの最初の部分では、接触は粘着によるものですが、2番目の部分では滑りが発生します（図2.7）。

ブレーキング時、純粋な転がり条件下では瞬間の転がり半径は車輪の外周半径より小さくなり、ブレーキング力の増加とともに転がり半径が車輪の半径を上回るまで増加します（車輪をロックする急激な停止では、この半径は無限大になります）。パッチの最初の部分では、接触は接着によるものです。ある時点で、前進速度と周速度の差が接着条件下で生成されるせん断応力を上回り、このため、滑り領域が生成されます。滑り領域の長さは、おおよそブレーキング力に比例します（図2.8）。

2.4.1 非線形モデル

トラクション時およびブレーキング時の両方の縦方向の力は、荷重に対して一次近似で比例します。縦方向のブレーキング / 駆動力係数と荷重（正規化された縦方向の力）の比率 $\mu$ は、縦方向の ブレーキング / 駆動力係数 と呼ばれます。

ノミナル荷重 $N$ における縦方向の力は、マジックフォーミュラによって記述できます。

係数 $D_\kappa = \mu p$ は、ブレーキング / 駆動力係数 のピークを表し、積 $D_\kappa C_\kappa B_\kappa$ は縦方向のスリップ剛性です。

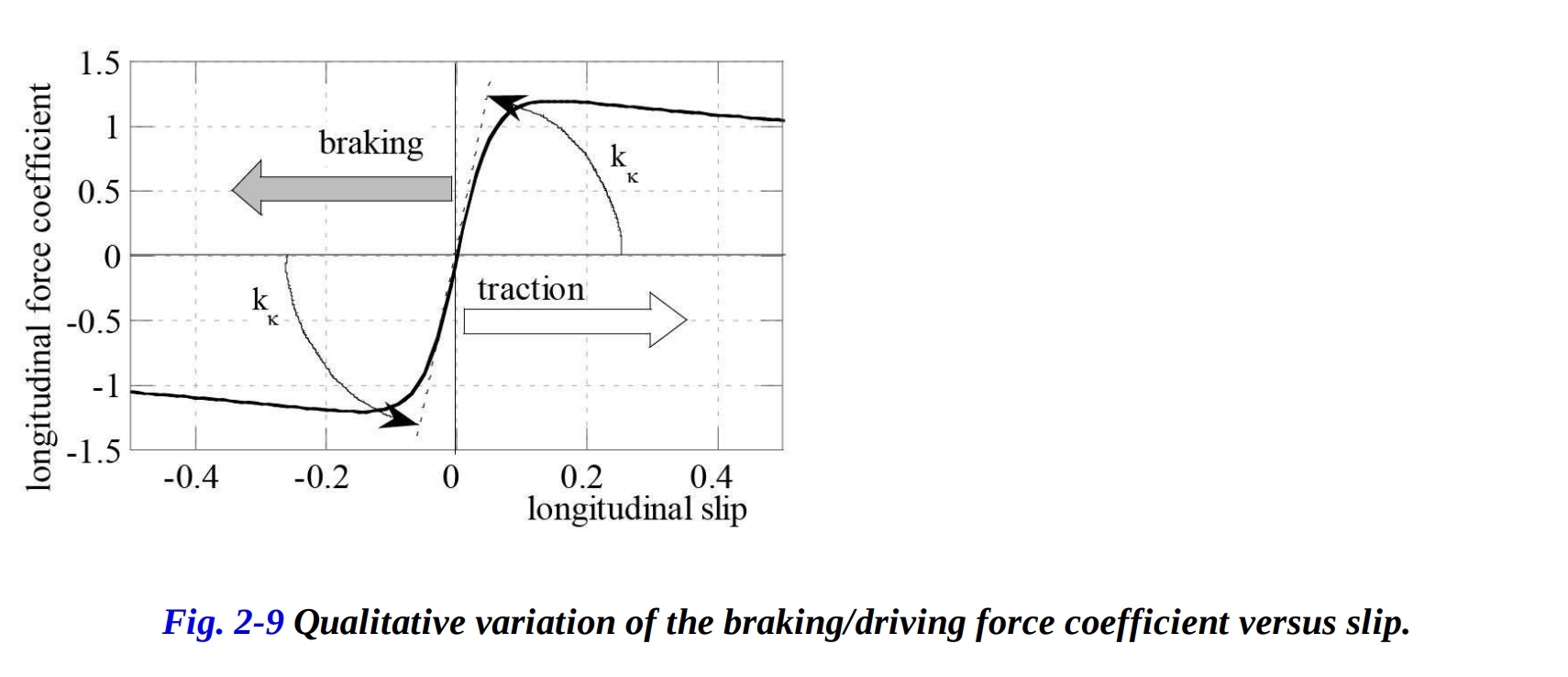
図2-9は、縦方向の力と法線荷重の比率を、縦方向のスリップの値の変化に対する定性的な観点から示しています。最大値（ブレーキング/駆動トラクション係数）は、道路状況に強く依存します。

2.4.2 線形モデル

ブレーキングおよび推進フェーズにおける力は、次のような線形方程式によって表すことができます。

ここで、

は、次元の滑りに対する剛性 $N$ を示し、

は、無次元の長手方向の滑り剛性を表します。

縦方向の剛性 $k_{\kappa}$ （滑りがゼロの時の勾配）の値のオーダーは、12から30の範囲にあります（無次元値）。

（例 2）

81 kW の出力（110 HP）を持つ車両が、最大速度 270 km/h（75 m/s）に達するとします。この速度に達するために必要な駆動力を求めます。次に、後輪に全荷重がかかった状態で最大の駆動力を仮定し、駆動力係数を求めます。

必要な駆動力は、出力と速度の比率に等くなります：

駆動力係数は次のようになります：

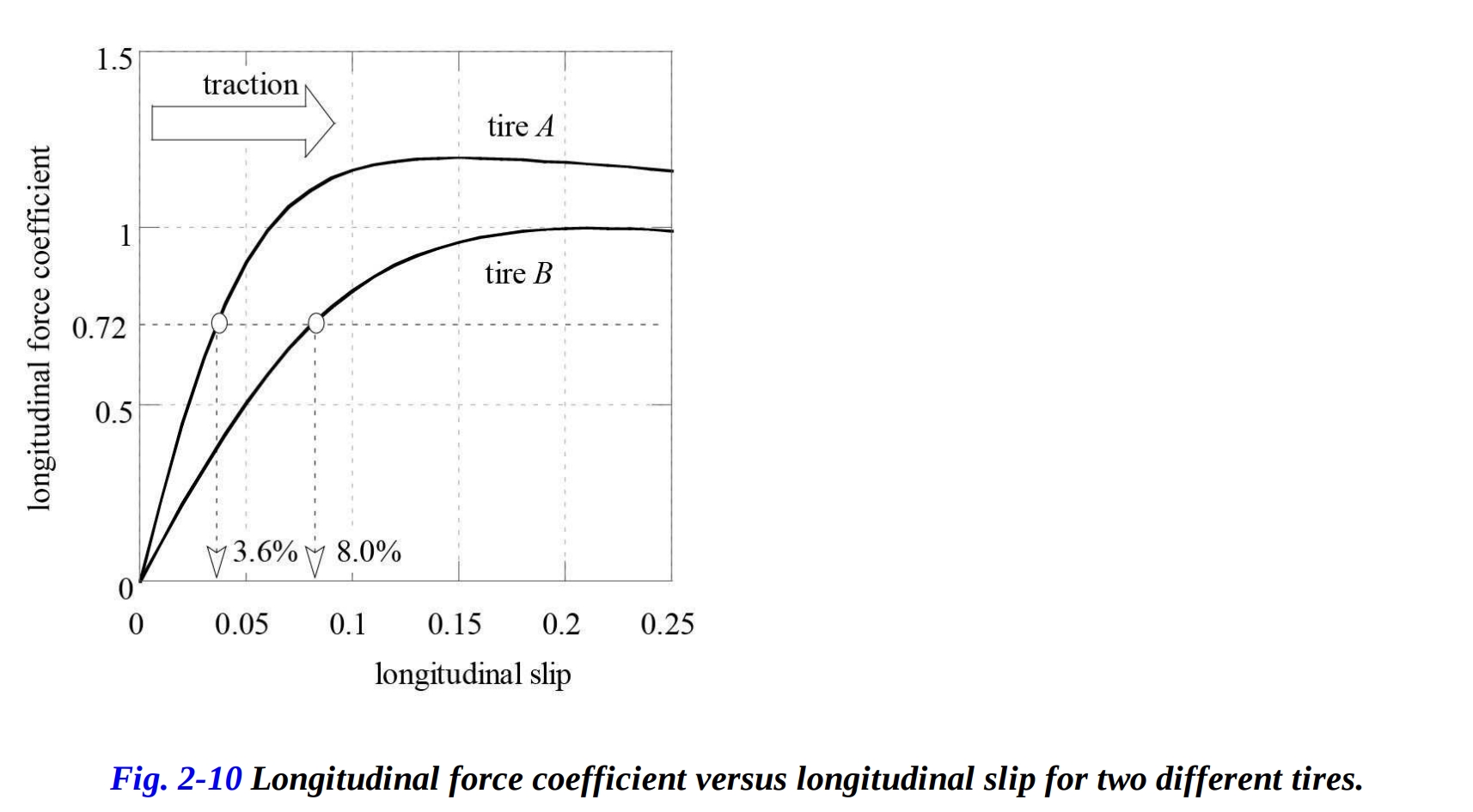
この正規化された縦方向の力を生じさせるために必要なスリップは、スリップに関する縦方向力係数の変動がわかっていれば決定できます。必要なスリップの値はタイヤの種類に依存します。図2-10に示されている2つの曲線では、摩擦係数 0.72 、タイヤ A の場合は 3.6％ のスリップ、タイヤ B の場合は 8％ のスリップが得られます。タイヤ B は、同じ駆動力を生成するために必要なより大きな縦方向スリップのため、タイヤ A よりも速く摩耗します。

2.5 横力

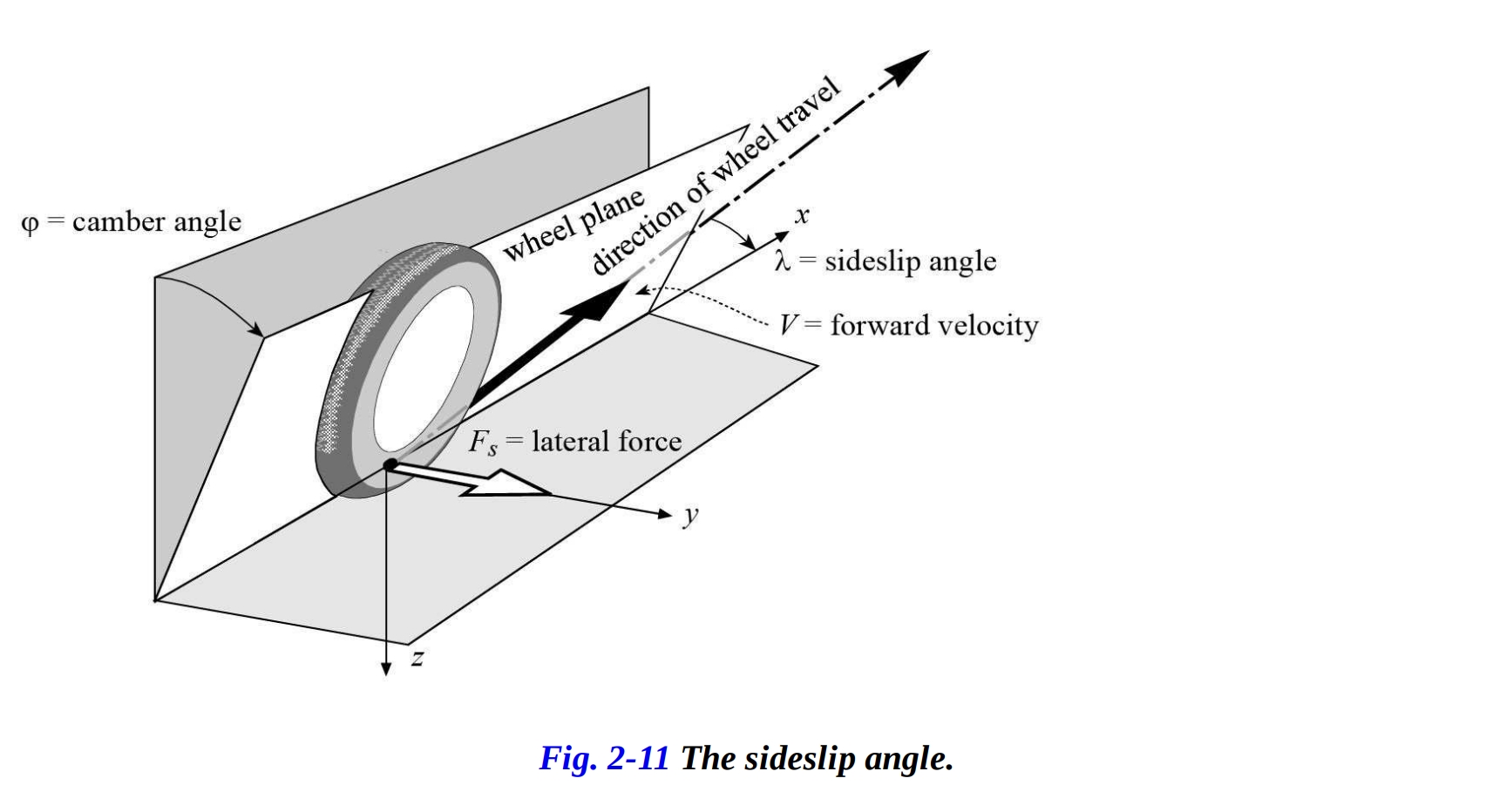
タイヤが地面に及ぼす横力は、サイドスリップアングル $\lambda$ とキャンバ角 $\varphi$ の両方に依存しています。サイドスリップアングルは、進行方向と車輪面が路面と交わる点との間の角度として定義されます（図2-11参照）。サイドスリップ力はタイヤのカーカスの歪みに依存し、一方、キャンバ力は主に幾何学に依存します。

タイヤは地面と接触すると変形し、タイヤの特性、ロール角、サイドスリップアングル、荷重、空気圧などの外部要因に応じて形状と寸法が可変のパッチ（contact patch）を生成します。横力やブレーキングまたは駆動トルクの存在は、このパッチにさらなる変形をもたらします。一般的に、パッチはx軸とy軸に対して対称ではありません。

2.5.1 キャンバー角によって発生する横力

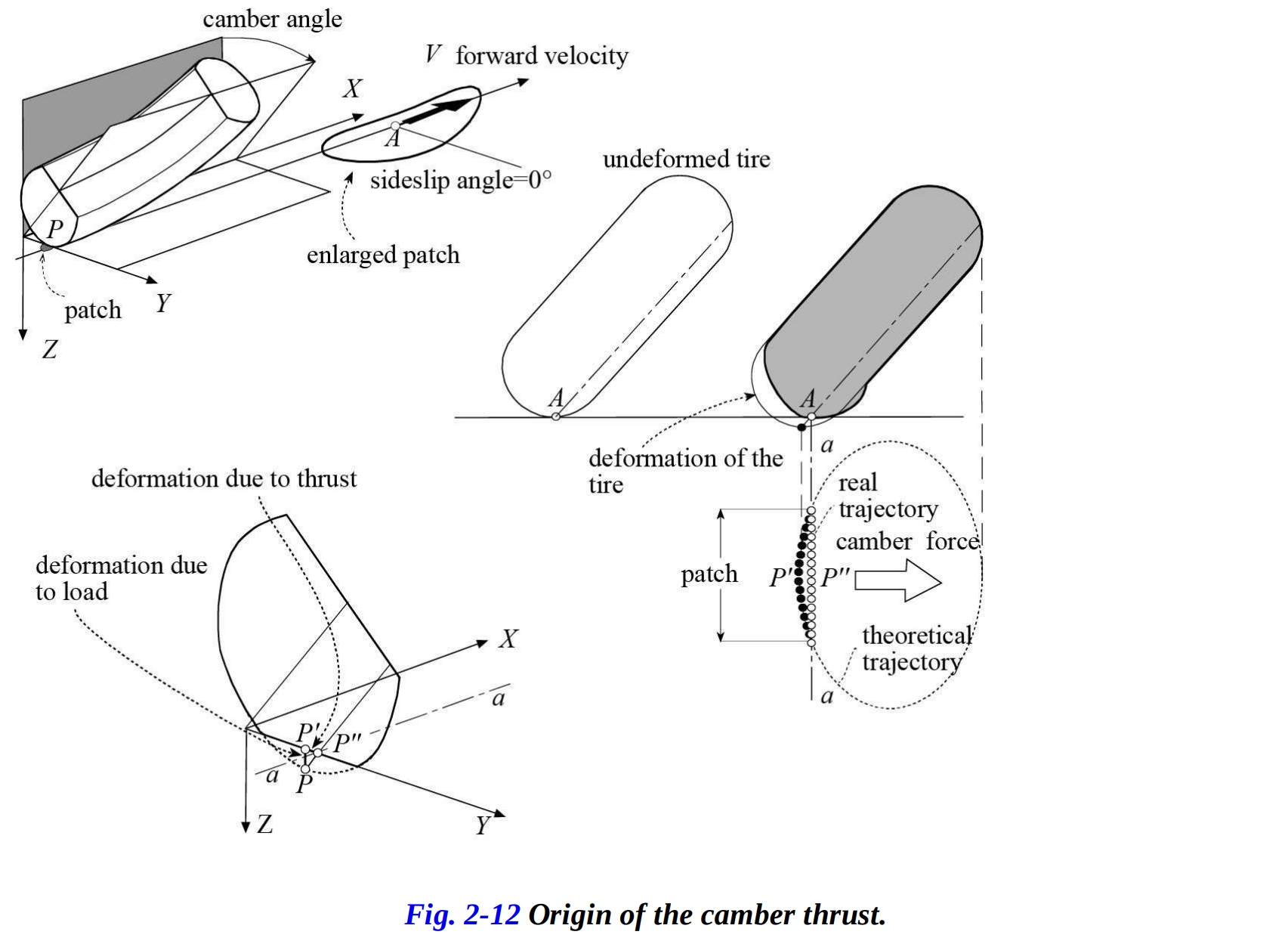
まず、設定されたキャンバ角度で傾いたタイヤの場合を考えてみましょう。このタイヤは、その平面の方向に前進し、サイドスリップアングルがゼロの場合です（図2-12）。タイヤカーカスが変形しない場合、パッチ上の点 $P$ は、空間上で円形の軌道を描き、その軌道の路面への投影は楕円曲線になります。したがって、それは道路で単一の接触点 $A$ で接触します。タイヤには横方向の変形がないため、キャンバ力は発生しません。

一方、タイヤのカーカスが変形する場合、接触面が広がり、地面と接触するときの点 $P$ は、上記の楕円軌道を離れ、車輪の進行方向に沿った直線軌道（図2-12の $a-a$ 線）になることを強いられます。

タイヤカーカスの変形 $PP''$ は、次の2つの段階で発生すると考えられます。まず、垂直荷重が垂直変形 $PP'$ を生成し、次にキャンバ力による横力が変形 $P'P''$ を生成します。キャンバに起因する横力は、特に小さなスリップアングルで重要です。

2.5.2 横滑りによって発生する横力

車輪が回転しながら横に滑るとします。この場合、接触パッチの形状は図2-13に示すように歪みます。 地面と接触するトレッド上にある点Pを考えます。点Pが点Aで地面と接触し、決定された点Bに移動すると、それは直線的な軌道を描きます。その速度は前進速度Vの方向を持ちます。点Bに達すると、カーカスとタイヤトレッド内のゴム要素の変形に起因する弾性復元せん断応力が、接着力よりも大きくなります。したがって、それを逆方向に変え、地面で滑らせて後方のエッジCに到達させます。 接触領域には次の2つの領域があります。

• 接着が行われる前方領域。
• スライドが発生する後方領域。

スライド領域はスリップアングルが大きいほど広がります。一定の側方力の限界値に達すると、全ての接触領域がスライド領域になります。

2.5.3 非線形モデル

図2-14は、正規化された横力とスリップアングル、およびキャンバー角に対する関係を定性的に示しています。特定のタイヤについて得られる力の最大値は、道路条件に強く依存しています。

これらの力は、[Cossalter et al., 2003]で記述された回転ディスク試験機によって測定されました。図2-15に示すように、ディスクは垂直軸を中心に回転し、安全歩行トラックが装備されています。試験対象の車輪はトラック上を転がり、関節アームによってキャンバー角とスリップアングルを設定できるように配置されます。

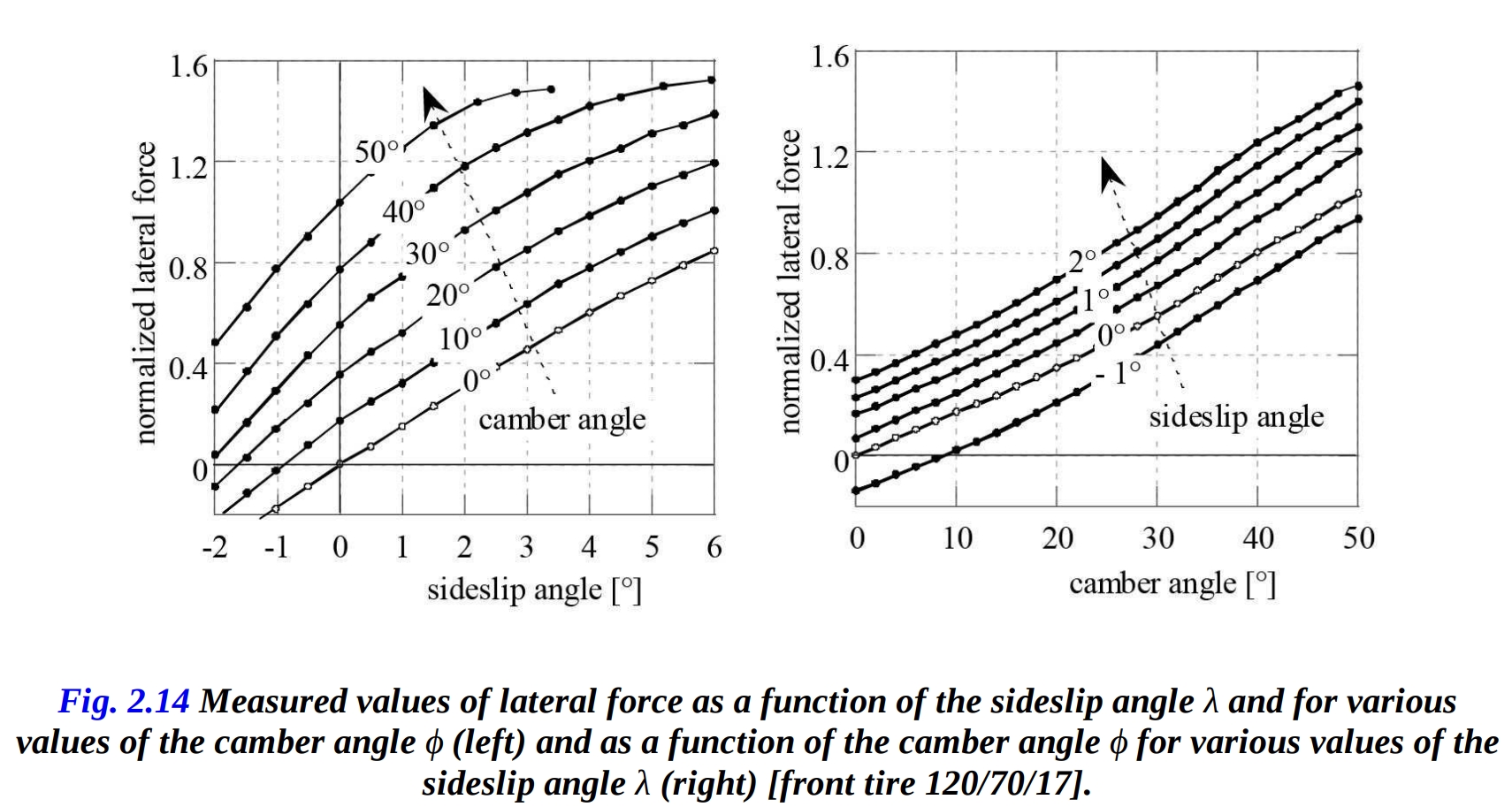
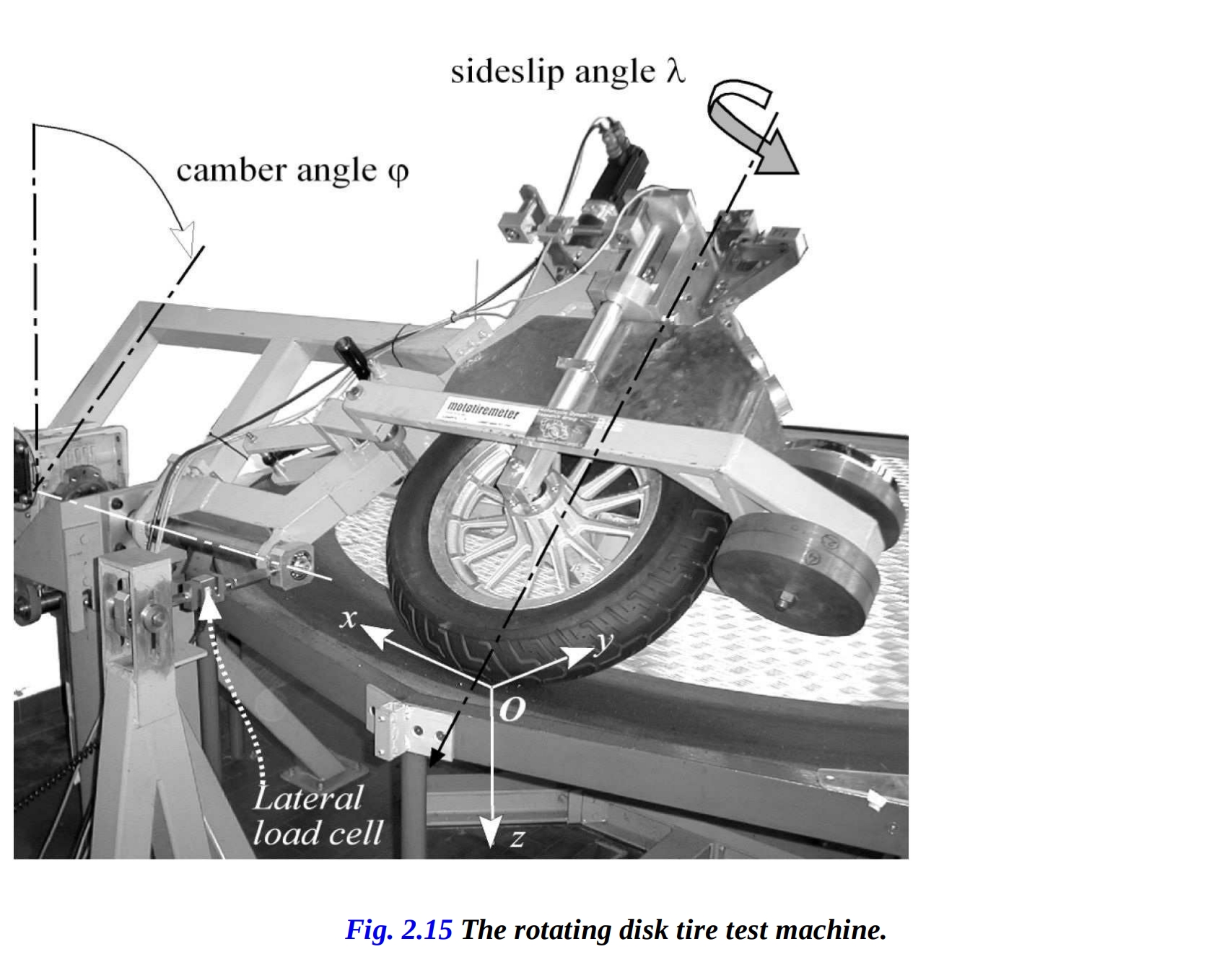
図に示されているように、横力は鉛直荷重、スリップアングル、およびキャンバー角の関数です。 コーニングとキャンバーの相互作用は、等価力アプローチを用いて以下の式で表すことができます:

このアプローチは、モーターサイクルタイヤに関する Pacejka の最新の定式化です[Pacejka, 2005]。 $Ds = \mu y$ は横力係数のピーク、$D_\lambda C_\lambda B_\lambda = k_\lambda$ はコーナリング剛性係数、$D_\varphi C_\varphi B_\varphi = k_\varphi$ はキャンバー剛性係数です。

2.5.4 線形モデル

タイヤと路面との接触力は、スリップアングルとキャンバー角に依存しています。小さなスリップアングルでは、スリップアングルに対する依存性がほぼ線形であり、キャンバー成分はほぼキャンバー角の線形関数です。 小さなスリップアングルと限られたキャンバー角のための横力は、次のような線形式で表されます:

図2-16は、左側には各種のキャンバー角の値に対するスリップアングルの関数としての正規化された横力の典型的な変化を、右側には各種のスリップアングルの値に対するキャンバー角の関数としての正規化された横力の変化を示しています。

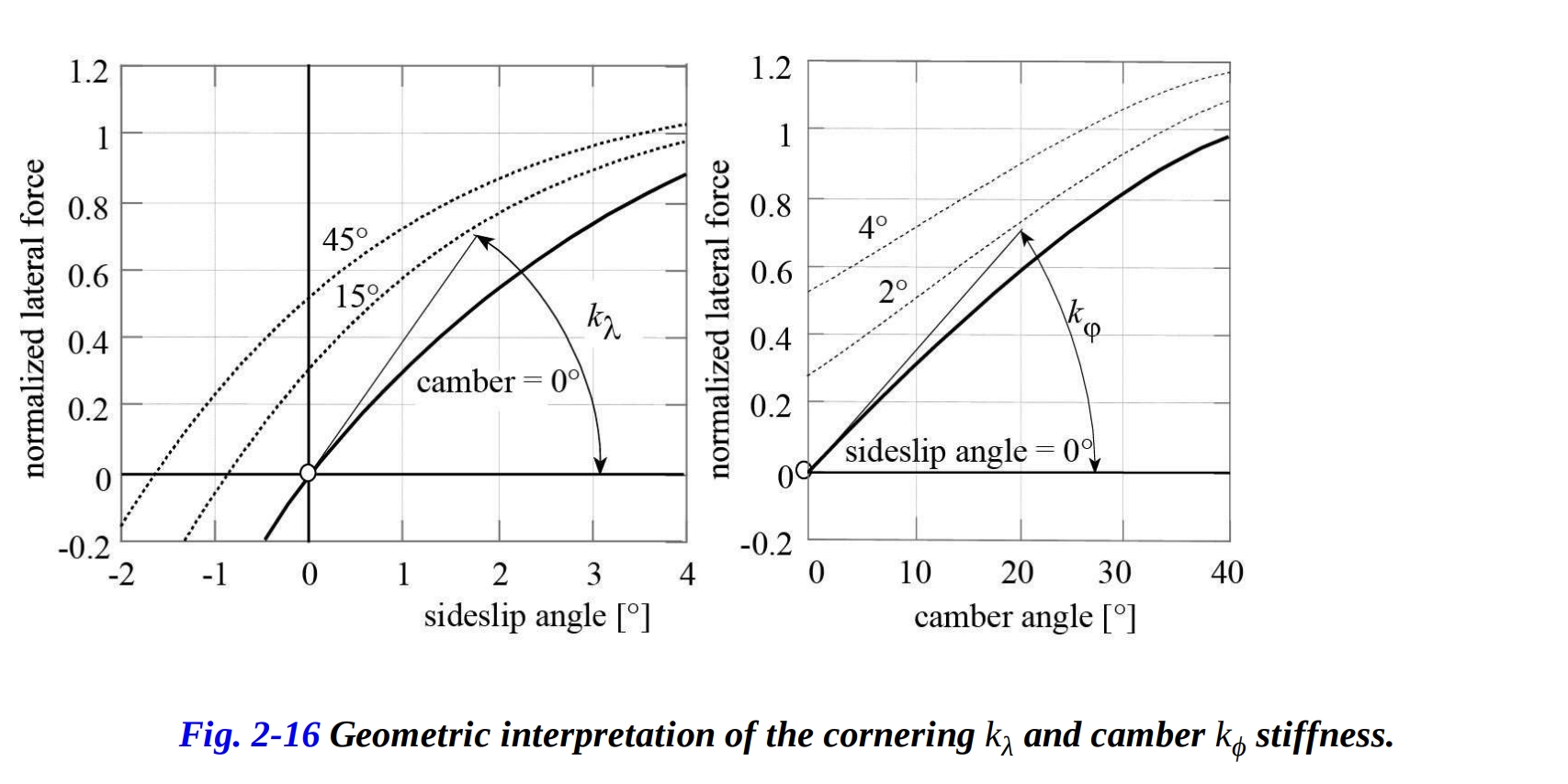
横力に関する限り、タイヤの特性はコーナリングとキャンバーの寸法剛性（N/rad）によって定義されます。

コーナリング剛性係数 $k_\lambda$ は、タイヤの特性の変化によって変動します。その可変範囲は約 $10 rad^{−1}$ から$25 rad^{−1}$ の値までです。

キャンバー剛性係数 $k_\varphi$ は、約 $0.7 rad^{-1}$ から$1.5 rad^{-1}$ の大きさです。 最大横力と垂直荷重との比率は、道路面がクリアで乾燥している場合には 1.3 から 1.6 の値に達することがあります。

2.5.5 モーターサイクルの平衡に必要な横力

曲がりの中で安定した状態のモーターサイクルを考えます。重心に作用する力のモーメントの平衡は、モーターサイクルの安定を確保するために必要な正規化された横力が、ロール角の正接に等しいことを示しています。これは図2-17で表されています。

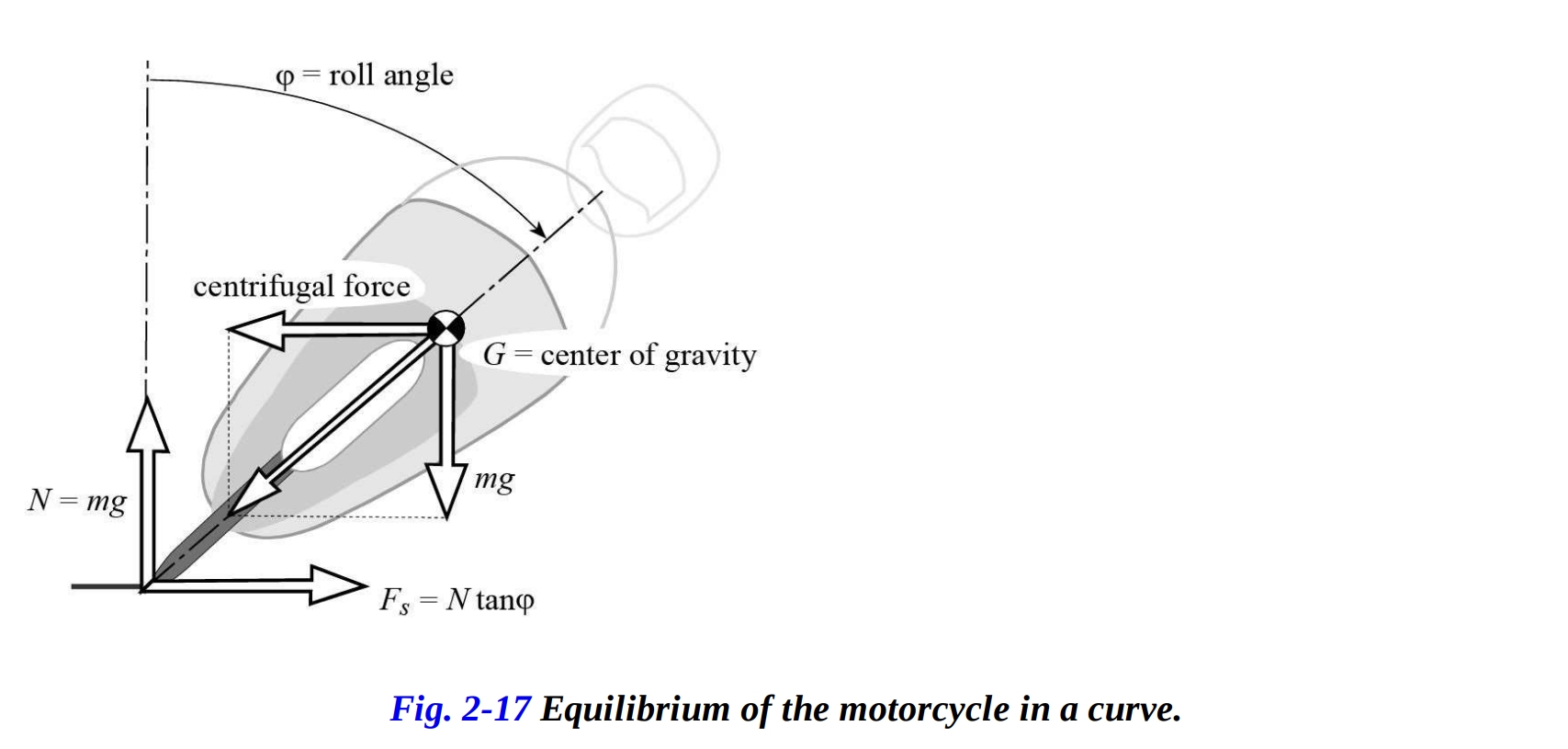
図2-18を考えましょう。右側のグラフは、特定のタイプのタイヤにおける、単独のキャンバーに起因する横力成分（直線）と、曲線上でのモーターサイクルの平衡に必要な横力（点線）を示しています。これらの力は垂直荷重 $N$ に関して正規化されています。左側のグラフは、横滑り角に対する正規化された横力を表しています。

直線はキャンバー力の変化を近似し、曲線 $\tan\varphi$ と交差する点がロール角 28° に一致していることが分かります。これは、0 から 28° の範囲では、平衡に必要な横力がキャンバーのみによって生成される推力よりも少ないことを意味します。生成される横力は、平衡に必要な横力とまったく等しくなければならないため、横力の減少は負の横滑り角を介して得られます。つまり、車輪はカーブの内側に向かって横方向の速度成分を持ちます。

例えば、図2-18では、キャンバー角が 10° の場合、生成される力と必要な力が等しくなるのは、負の横滑り角が 0.3° のときです（点$A$ ）。キャンバー角が 28° の場合、横滑りはゼロです（点$B$ ）。キャンバー角が 28° を超える値では、キャンバーのみによって生成される横力はモーターサイクルの平衡に十分ではなく、したがってタイヤの横滑り（正の横滑り）で横力を増加させる必要があります。

このような特徴的なタイヤの挙動は、特定のロール角度に達するまで、ほぼ全てがキャンバー成分によるものです。この成分は、スリップ成分よりも早く現れるため、安全性において基本的な役割を果たします。キャンバー成分は、カーカスの変形に依存するため、角度の変化が速いですが、コーナリング成分はスリップアングルに依存するため、発生に時間がかかります。

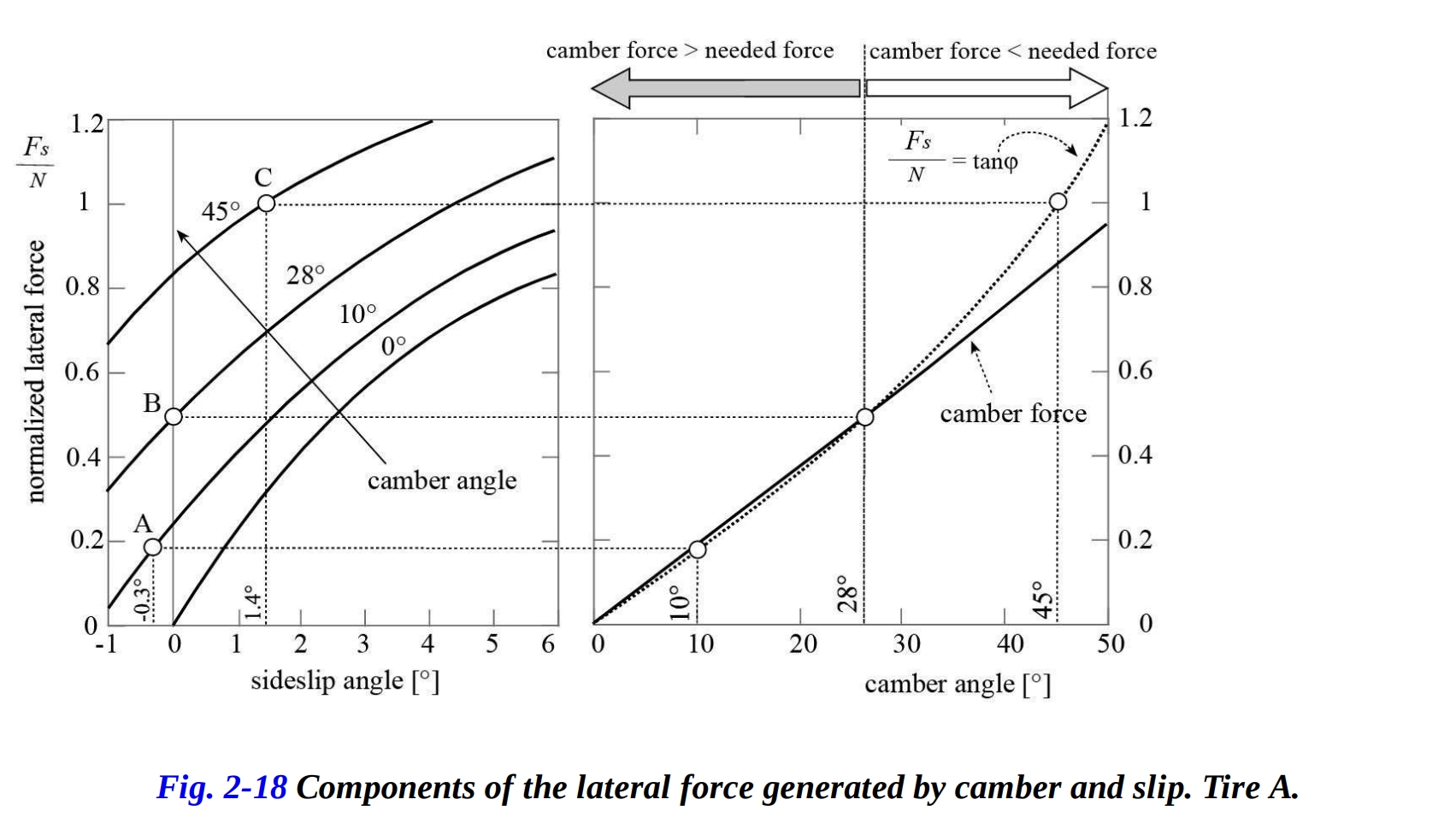
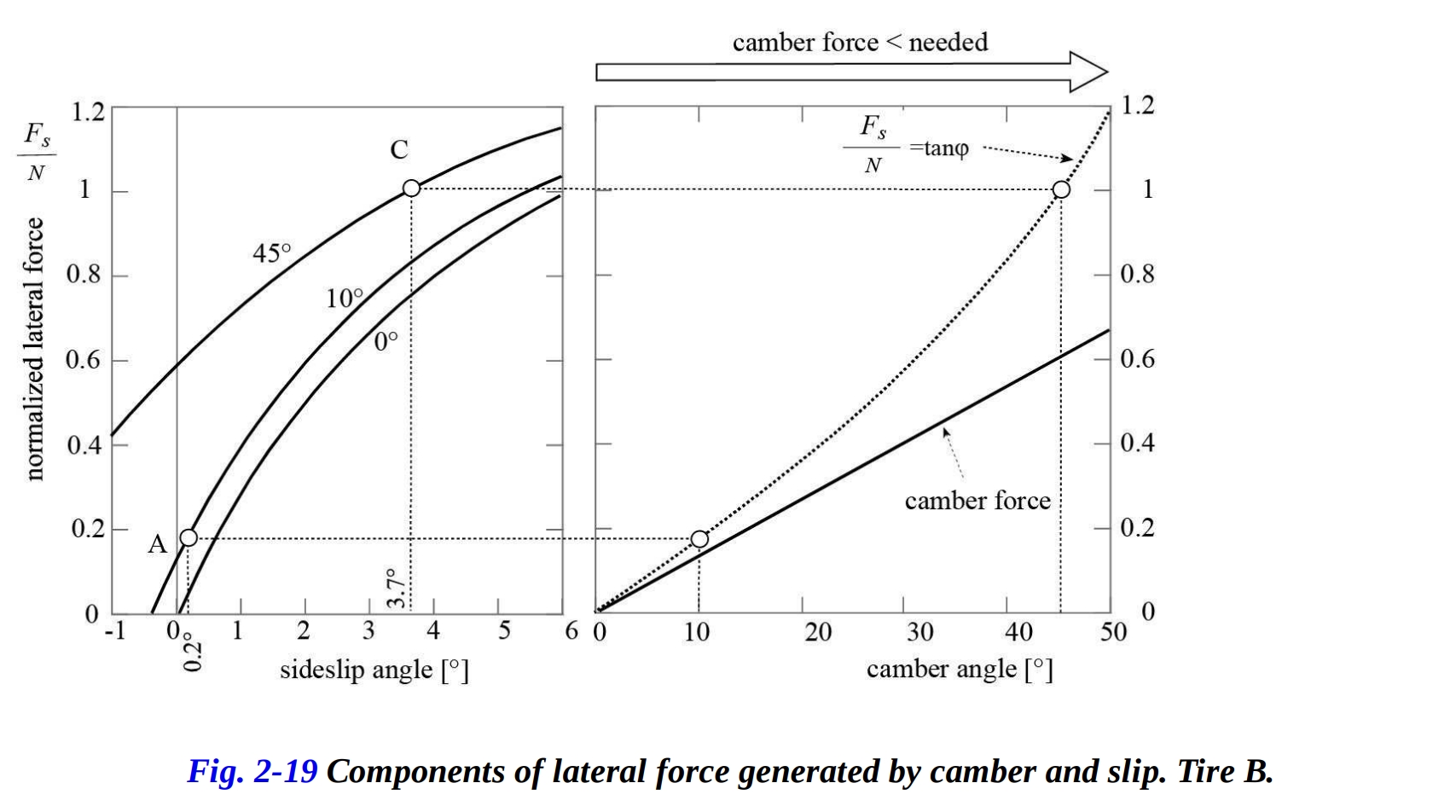
図2-19のグラフを考えてみましょう。これは異なるタイプのタイヤを示しています。この場合、キャンバー推力は常に、均衡に必要な横力を下回っています。つまり、均衡に必要な追加の横力を生成するためには常に横滑りが必要です。横力、それらが生成される方法、およびキャンバー角とスリップアングルに対する依存性は、バイクのアンダーステアやオーバーステアの挙動において基本的な役割を果たします。

もし、前輪の横力の生成に必要なスリップアングルが後輪の横力の生成に必要なものよりも大きければ、ロール角が増加するにつれて、バイクは前輪でより多くスリップしやすくなります。この挙動は、車両がアンダーステアになる原因となります。一方、後輪のスリップが前輪よりも大きい場合、挙動はオーバーステアとなります。スリップアングルが等しい場合は、中立挙動となります。これらの考察によれば、タイヤの理想的な挙動は、スリップアングルがゼロのときであり、つまり、均衡のために必要な横力がキャンバーだけで生成されるときです。

2.5.6 横力の荷重、圧力、温度依存性

タイヤの横グリップ能力は、キャンバー角とスリップアングルに対する横力をグラフ化するとよく分かります。図2.20では、異なるタイプのフロントタイヤとリアタイヤについてグラフ化したものです。

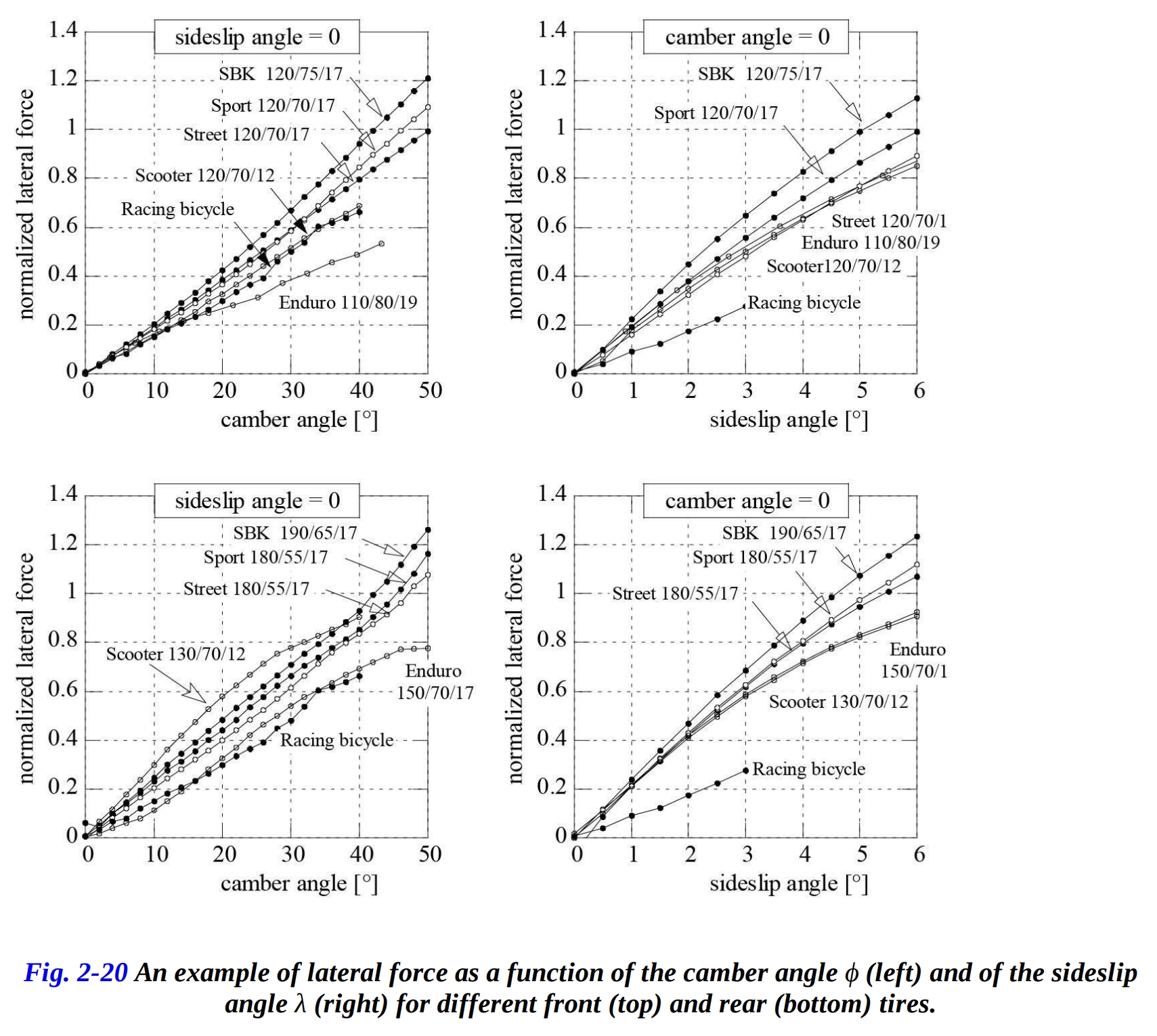
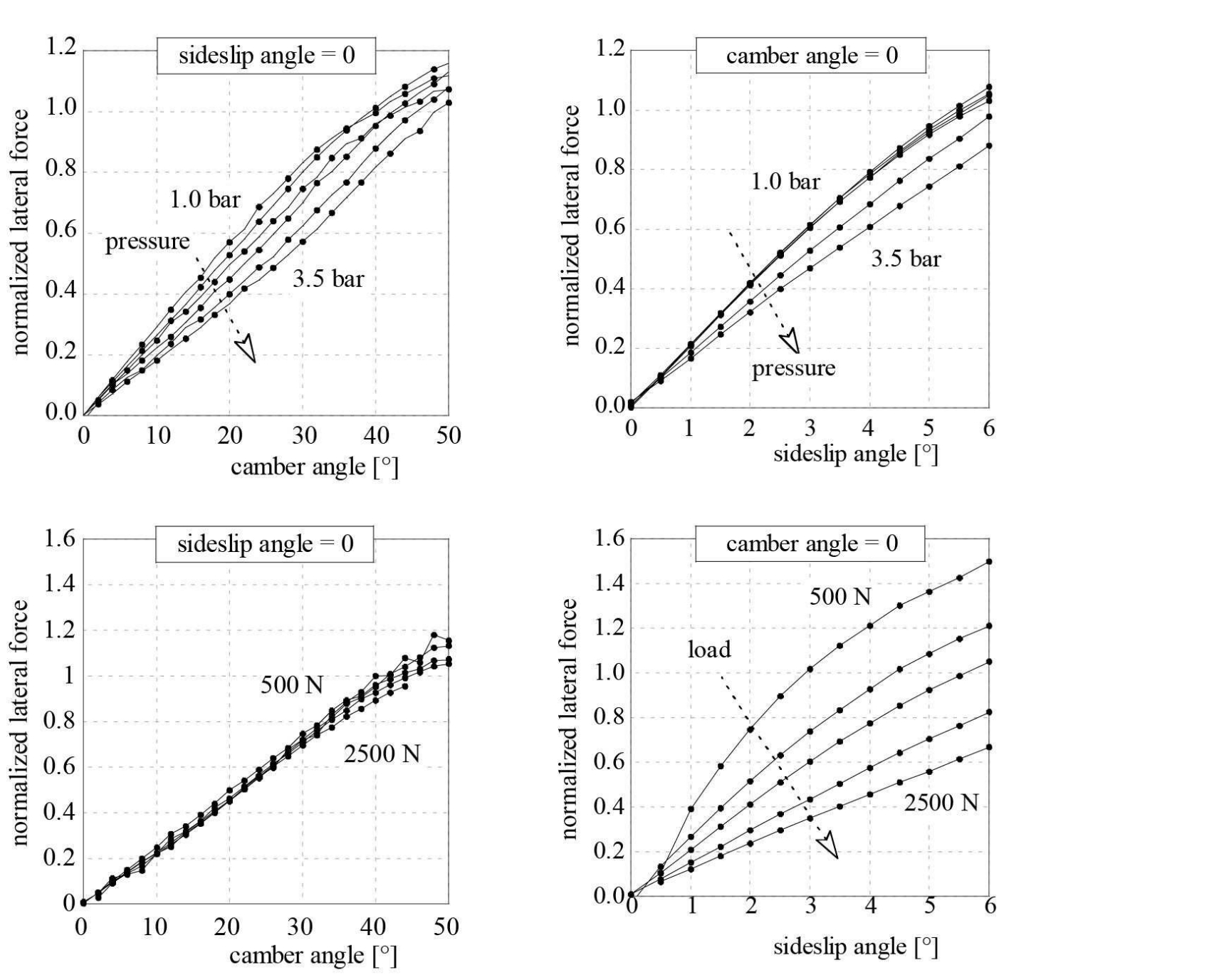
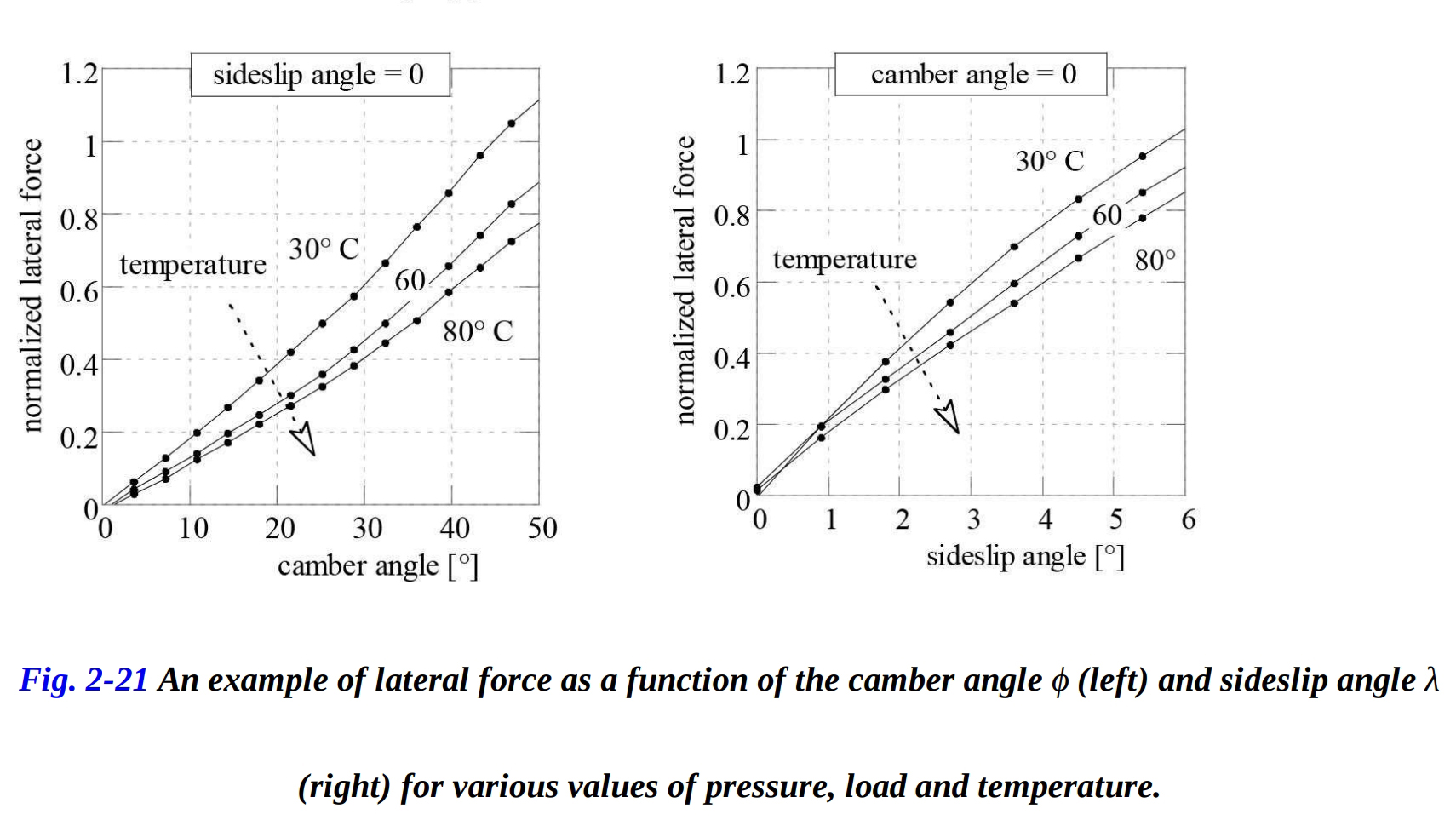
図2-21は、異なる空気圧、鉛直荷重、およびカーカス温度の値に対する、スリップアングルとキャンバー角に対する正規化横力を示しています。 コーナリング剛性は、タイヤの横剛性やラジアル剛性と混同すべきではありません。横剛性は、横力とカーカスの横変形との関係です。これはタイヤの構造的特性に依存します。その値のオーダーは、100 から 200 kN/mです。タイヤのラジアル剛性は、鉛直荷重と鉛直変形との関係であり、その値は 100 から 350 kN/mの範囲にあります。空気圧と前進速度は、これらの構造剛性の両方に影響を与えます。

鉛直荷重の増加により、コーナリング剛性係数が減少しますが、キャンバー剛性係数はほとんど影響を受けません。空気圧の増加により、コーナリング剛性係数が減少し、キャンバー剛性係数もある程度減少します。断面積の大きいタイヤ、または断面半径の大きいタイヤは、通常、大きなコーナリング剛性係数を持ちます。温度の上昇により、コーナリング剛性係数とキャンバー剛性係数の両方が減少しますが、最大横力と鉛直荷重の比の最大値が増加します。

2.5.7 過渡状態での横力

横方向の力は、即座に発生するわけではないと述べました。その発生には、タイヤのコーナリング特性と横剛性により決まる、一定の距離を走行する必要があります。 モータサイクルが最初に鉛直の平衡姿勢にあるとします。そのとき、ロール角とスリップアングルはゼロであり、それに対応する横方向の接触力もゼロです。

もしも、ロール角とスリップアングルにゼロ以外の値を即座に割り当てた場合、横方向の接触力は指定されたロール角とスリップアングルに対応する定常状態の値まで指数関数的に増加します。したがって、接触力は、それらの角度の変化に対して遅れて追従します。これは、カーカスの変形には時間がかかるためです。主にタイヤの形状に依存するキャンバー成分による力は、横滑りに起因するそれよりも早めに立ち上がります。

過渡状態でのタイヤの挙動は、図2-22のモデルによって表されます。このモデルは、ばね（剛性$k_s$ で表される[N/m]）とダンパー（減衰係数 $c$ で表される[kg/s]）が直列に配置されています。ばね剛性 $k_s$ はタイヤの横剛性を表し、主にタイヤのカーカスの形状と特性により決まります。一方、ダンパー $c$ は、タイヤが横滑りの状態での挙動を表します。タイヤのカーカスの慣性を無視すれば、コーナリング力は、タイヤの変形によって生成される弾性力と等しく、向きは逆です。

ここで、$\lambda' = \dot{y}/V$ は過渡状態のスリップアングルを表し、つまり接触パッチ（点$P$ ）のスリップアングルを示します。ここで、$y$ は接触パッチの横方向の変位であり、$y_i$ はホイール位置の変位です。

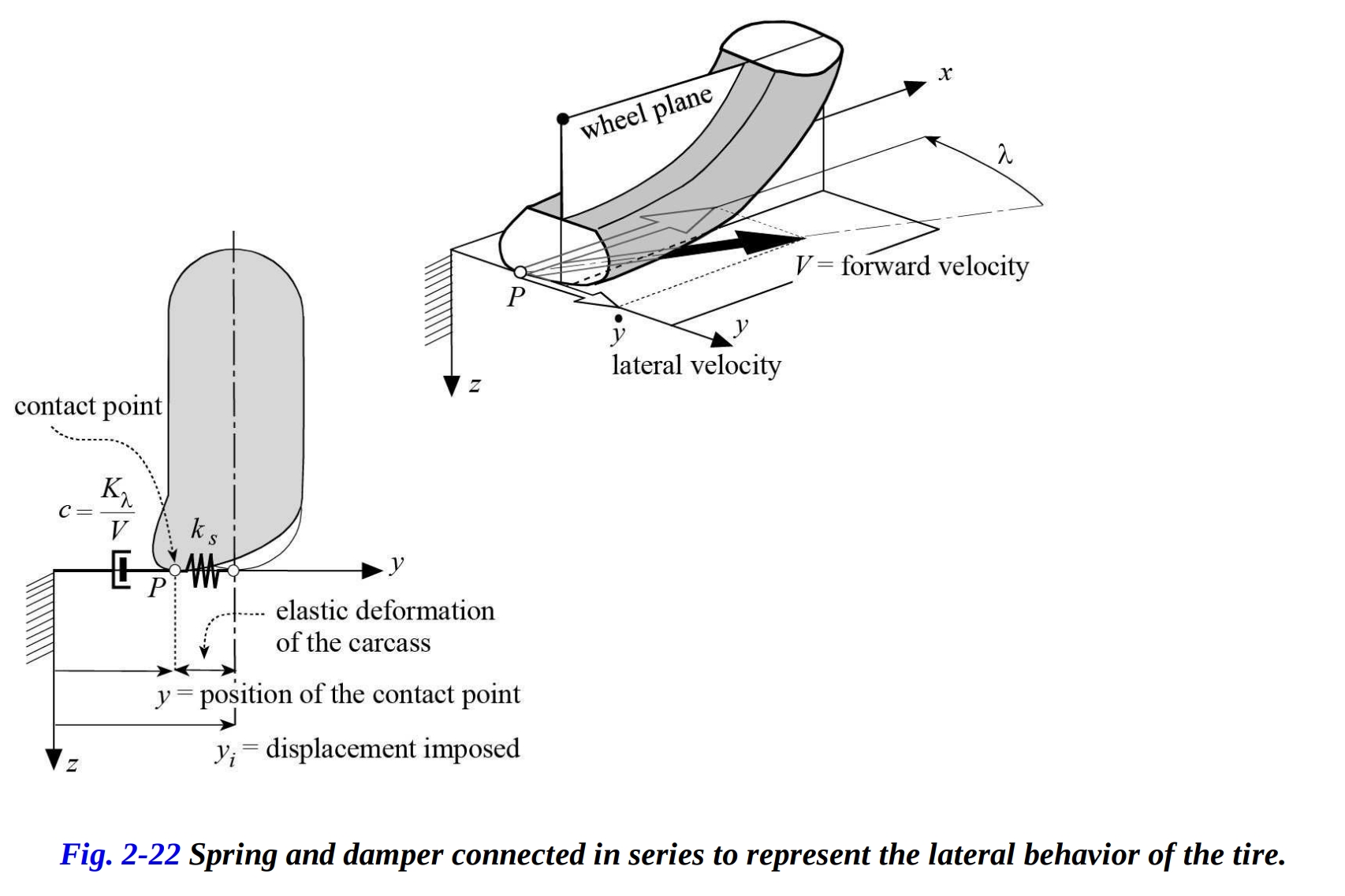
スリップ角と見かけの減衰係数を $c = K_\lambda / V$ とすると、以下のような方程式に表されます。

この微分方程式は、発生する横力の観点からも表現することができます。いくつかの操作を行った後、以下の式が得られます。ここで、$\lambda = \dot{y}_i / V$ は車輪のスリップ角を表します。

ここで、$L = K_\lambda / ks$ は緩和長を表します。 車輪が $t = 0$ で瞬時にスリップ角 $\lambda_0$ による横方向の動きを受けるとします。その場合、横力は指数関数的に増加します。

車輪が移動する距離 $x$ は、速度と時間の積であるから、次式を得ます。

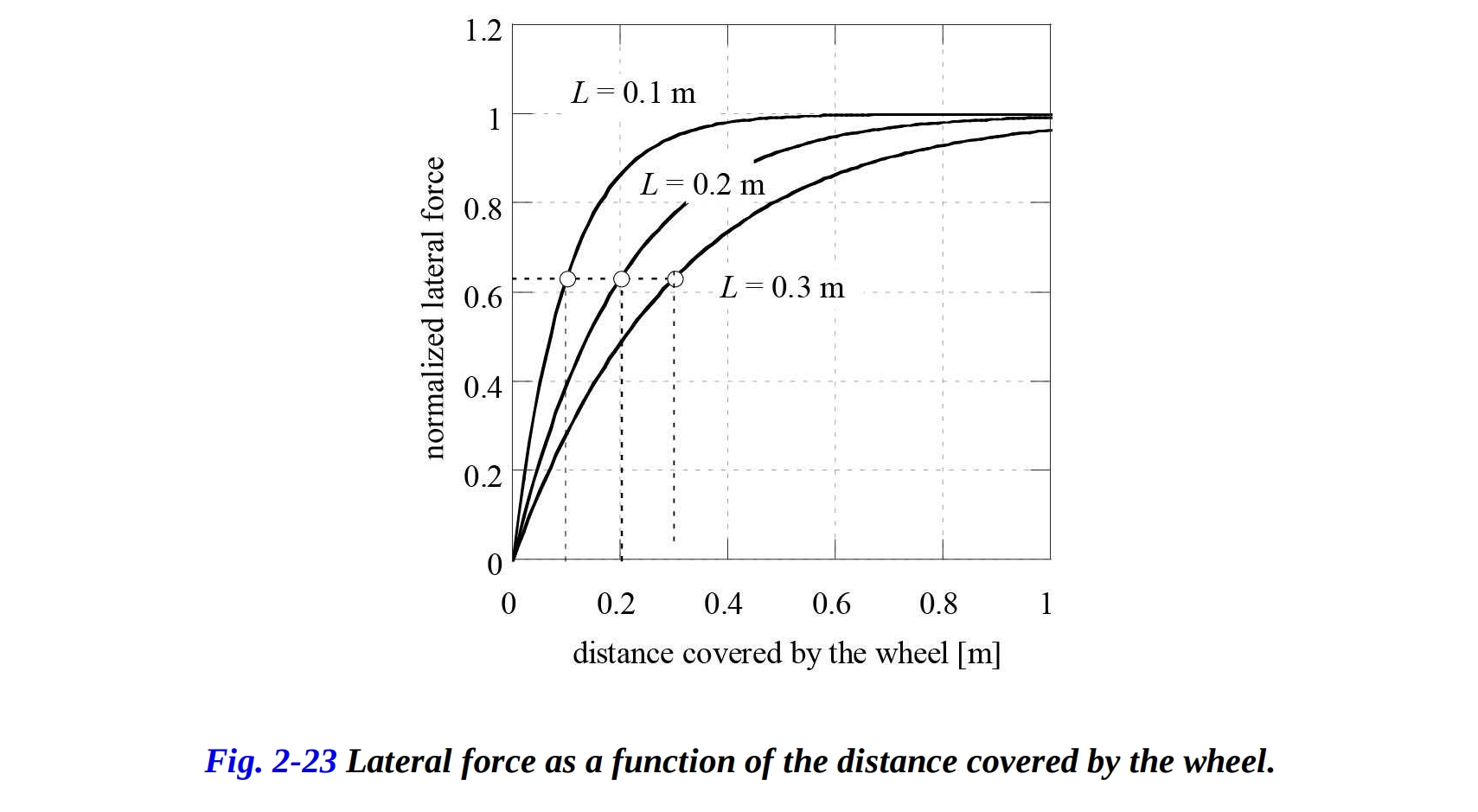
図2-3は、車輪がカバーする距離 $x$ の関数として、定常状態での値 $K_\lambda \lambda_0$ で正規化された横力の変化を示しています。原点を通る接線の傾きは、$k_s/K_\lambda$ と等しく、その逆数は緩和長と呼ばれます。

緩和長は、横力が定常状態の力の63％に達するまでに車輪がカバーする必要がある距離を表します。微分方程式を積分することで、滑り角に時間変化を割り当てると、横力が得られます。 カーブ力の緩和長の値は0.12〜0.45 mの範囲になります。小さい値は低速（20 km/h）に対応し、大きな値は非常に高速（250 km/h）に対応します。負荷がわずかに増加すると、緩和長もわずかに増加します。興味深いことに、緩和長は側滑角振動の周波数νと前方速度Vの比率に対してほぼ一定です。この比率はパス周波数と呼ばれ、前進運動の1メートルあたりのサイクル数を表します。 一方、実験結果では、キャンバ力の緩和長の値がほぼ無視できるとされることもあります。ただし、この振る舞いを検証するためにさらなる実験結果が必要です。

2.6 タイヤと路面の間に働くモーメント

2.6.1 自己調整モーメント（Self-alignment moment）

タイヤの横滑りによって生成される横せん断応力の分布は対称ではありません。そのため、横力は、道路面との接触点（中心点）から一定の距離だけずれて発生します。この距離$a_t$ は、タイヤのトレイルまたはニューマチックトレイルと呼ばれます。図2-24から明らかなように、横力はタイヤを回転させるモーメントを生成し、横滑り角を減少させる方向に回転します。このため、このモーメントはタイヤの自己調整モーメントと呼ばれます。

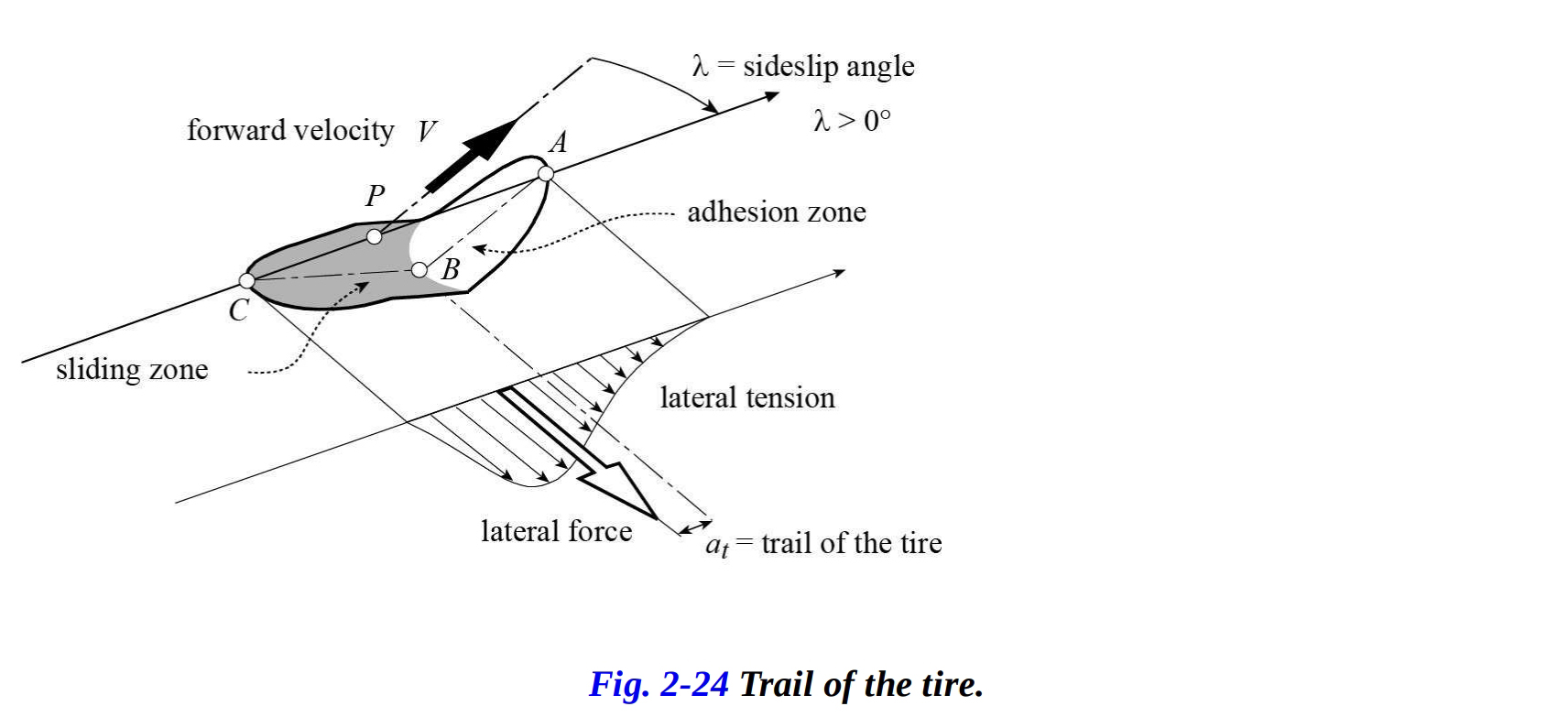
自己調整モーメント $M_z$ は、コーナリング力 $F_s$ とタイヤのトレイル $a_t$ の積で表されます。

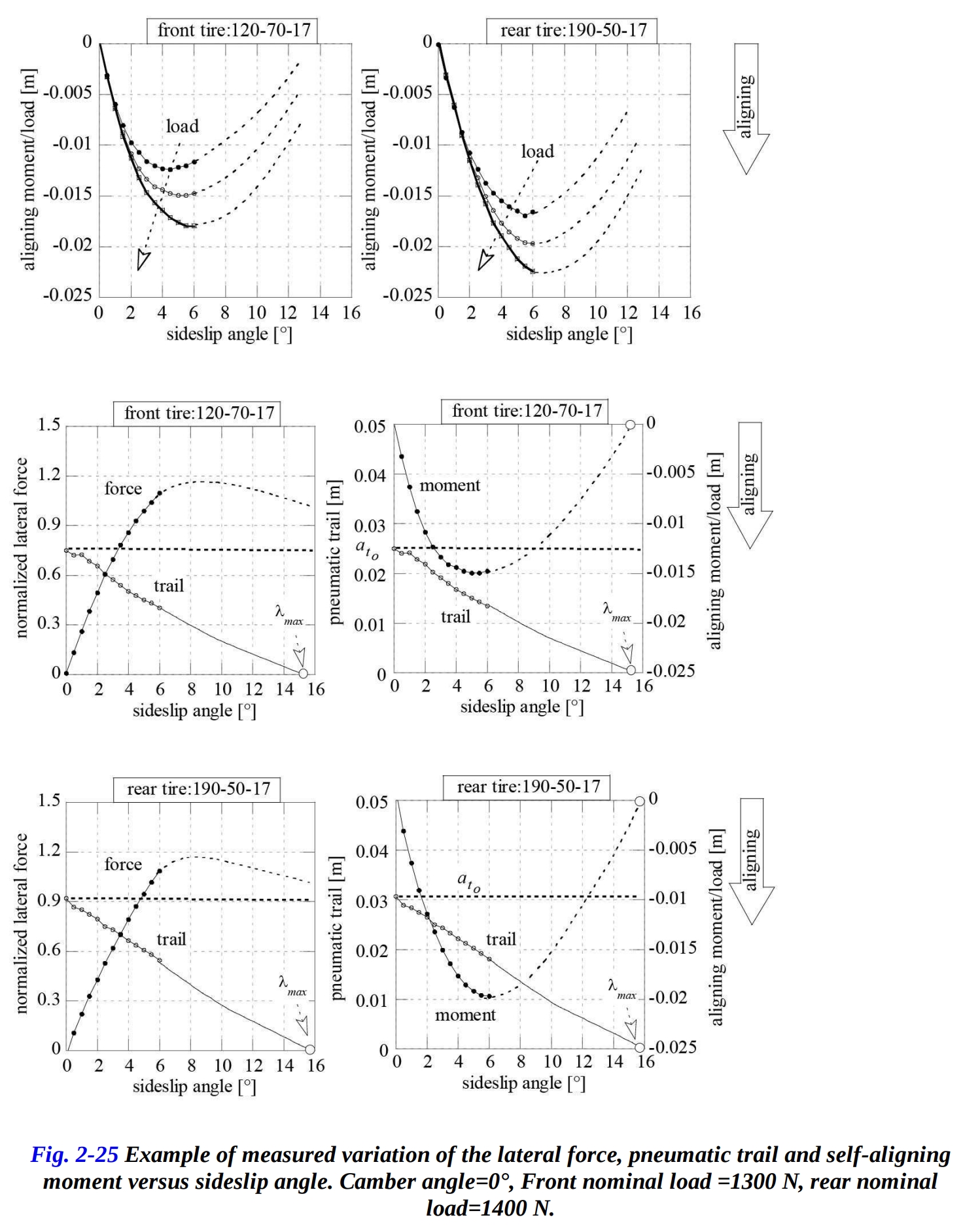
実験結果によれば、トレイルはスリップ角がゼロのときに最大であり、スリップ角が増加すると減少（$a_t \geqq 0$ ）し、垂直荷重が増加すると増加します。スリップ角の関数として以下の線形方程式で近似できます。

ここで、$a_{t_0}$ はトレイルの最大値を表し（$a_{t_0}$ は1.5〜5 cmの範囲です）、$\lambda_{max}$ はトレイルがゼロになるスリップ角を表します。 図2-25は、スリップの関数としての横すべり力、ニューマチックトレイル、および自己整列モーメントの典型的な変化を示しています。スリップ角が $\lambda_{max}$ の値（約15°）に達すると、モーメントはゼロになります。なぜなら、横力がパッチの中心を通過するためであり、パッチ全体がスライディングゾーンになっているからです。

2.6.2 ねじれモーメント

車輪軸に関する角速度 $\omega$ で転がる傾いた車輪を考えます（図2-26）。

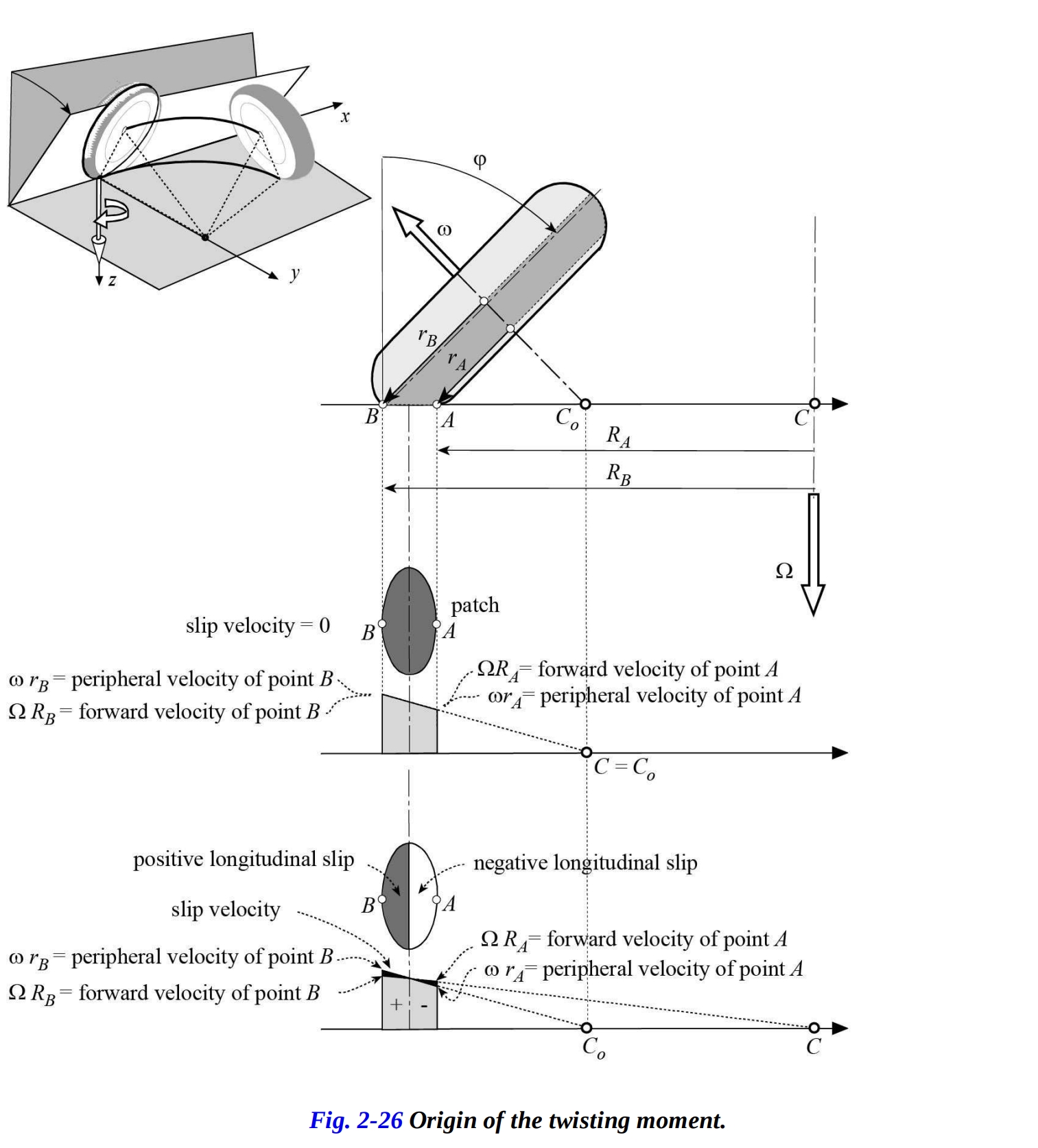
車輪の軸と路面の交点を $C_0$ で示します。もし円軌道の中心点 $C$ が車輪の交点 $C_0$ と一致している場合、縦方向のすべりなしに運動しています（運動学的条件下）。実際、パッチの一部であるタイヤの点 $A$ と点 $B$ の周速度は、角速度 $\Omega$ で点 $C$ を中心に回転する車輪の前進速度に等しくなります。

現実には、自由に転がる場合、曲線の中心 $C$ は常に点 $C_0$ の外部に位置します。 パッチの中心点では周速度が前進速度に等しいと仮定します。

パッチの最外部領域では周辺速度が前進速度よりも大きく、一方、パッチの内部領域では逆が真です。したがって、スリップが発生し、パッチ内には2つのゾーンが区別されます：正の長手方向スリップ速度を持つゾーンと、負の長手方向スリップ速度を持つゾーンです。したがって、外部ゾーンには前方向のせん断応力が生じ、内部ゾーンには後方向のせん断応力が生じます。 これらのせん断応力は、車輪を曲率半径の小さい軌道に沿って移動させる捩りモーメントを生成し、それにより車輪をアライメントからずらすように作用します。捩りモーメントは、おおよそキャンバ角に比例します。その典型的な変化を図2-27に示します。

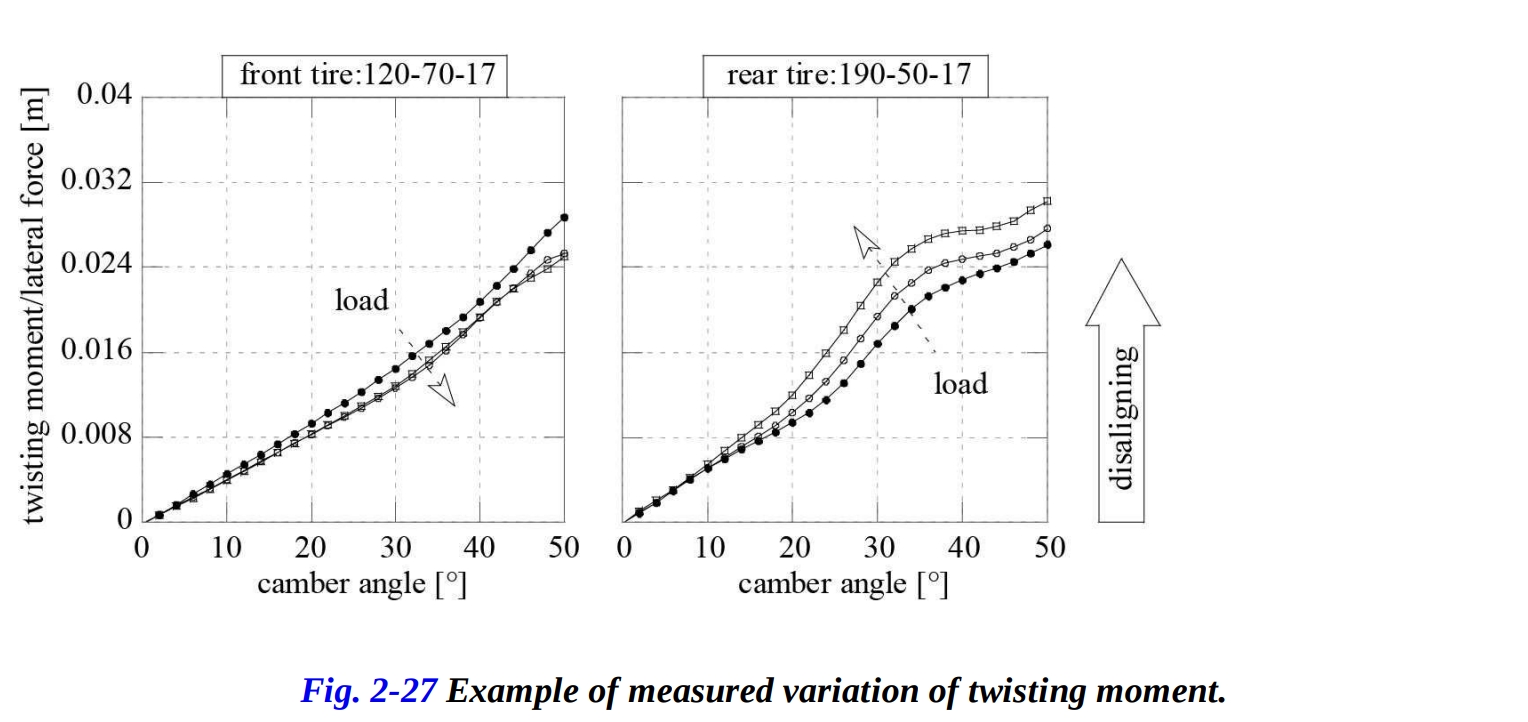
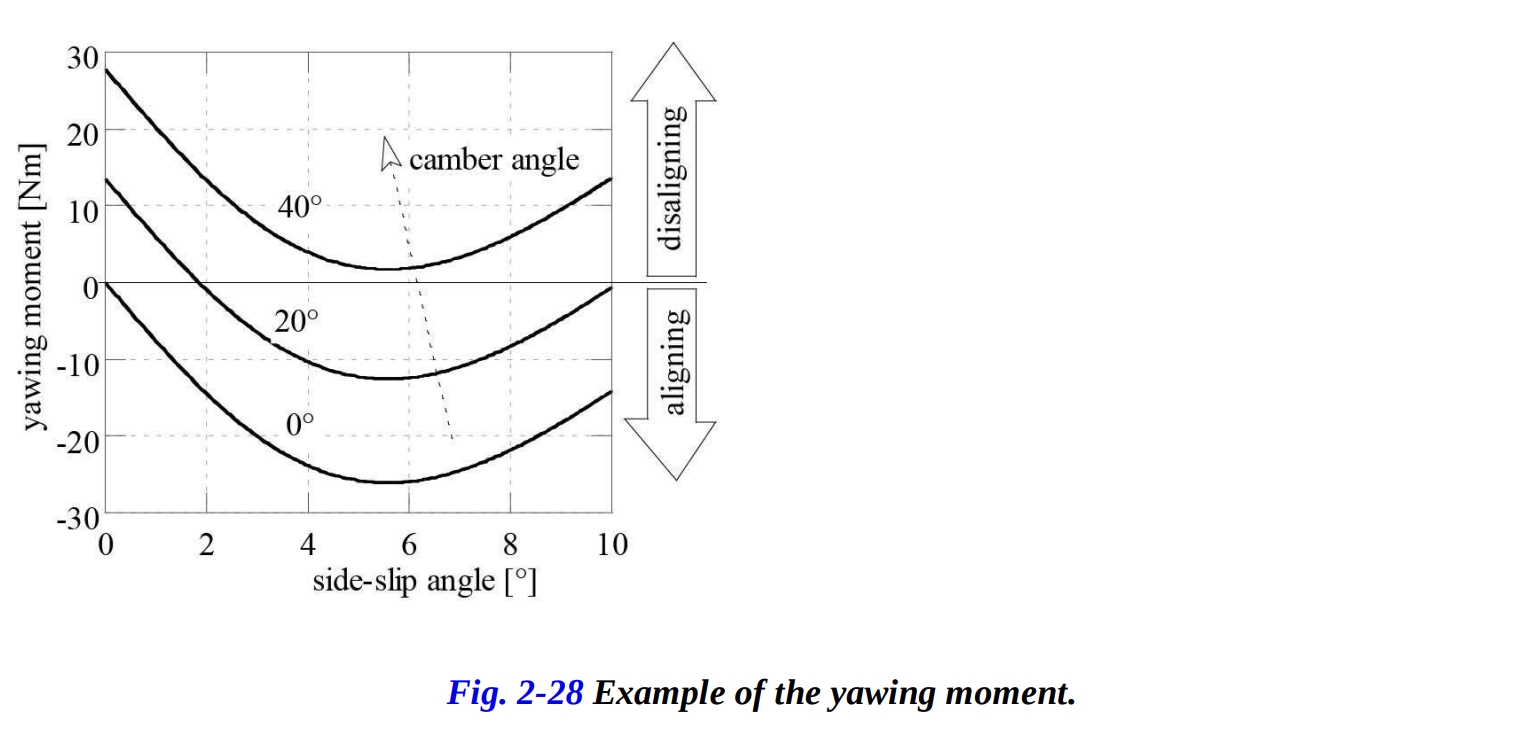
車輪には、反対符号の2つのモーメントが働きます：自己整列モーメントと捩りモーメントです。その合計は車輪のヨーモーメントを定義し、その横ずれ角に対する定性的な変化を図2-28に示します。ヨーモーメントMzは、スリップ角とロール角がゼロのときにゼロになり、ロール角が増加するにつれて増加し、スリップ角がλ = 2°から6°の間に最小値を持ちます。

2.6.3 駆動力または制動力によって発生するトルク

駆動力は、タイヤの平面を進行方向に沿ったモーメントを生成し、一方、制動力はその逆の符号のモーメントを生成します。したがってアライメントからずらします。縦方向の力はタイヤの横変形に依存します。

ここで、$k_s$ はタイヤのカーカスの横剛性です。

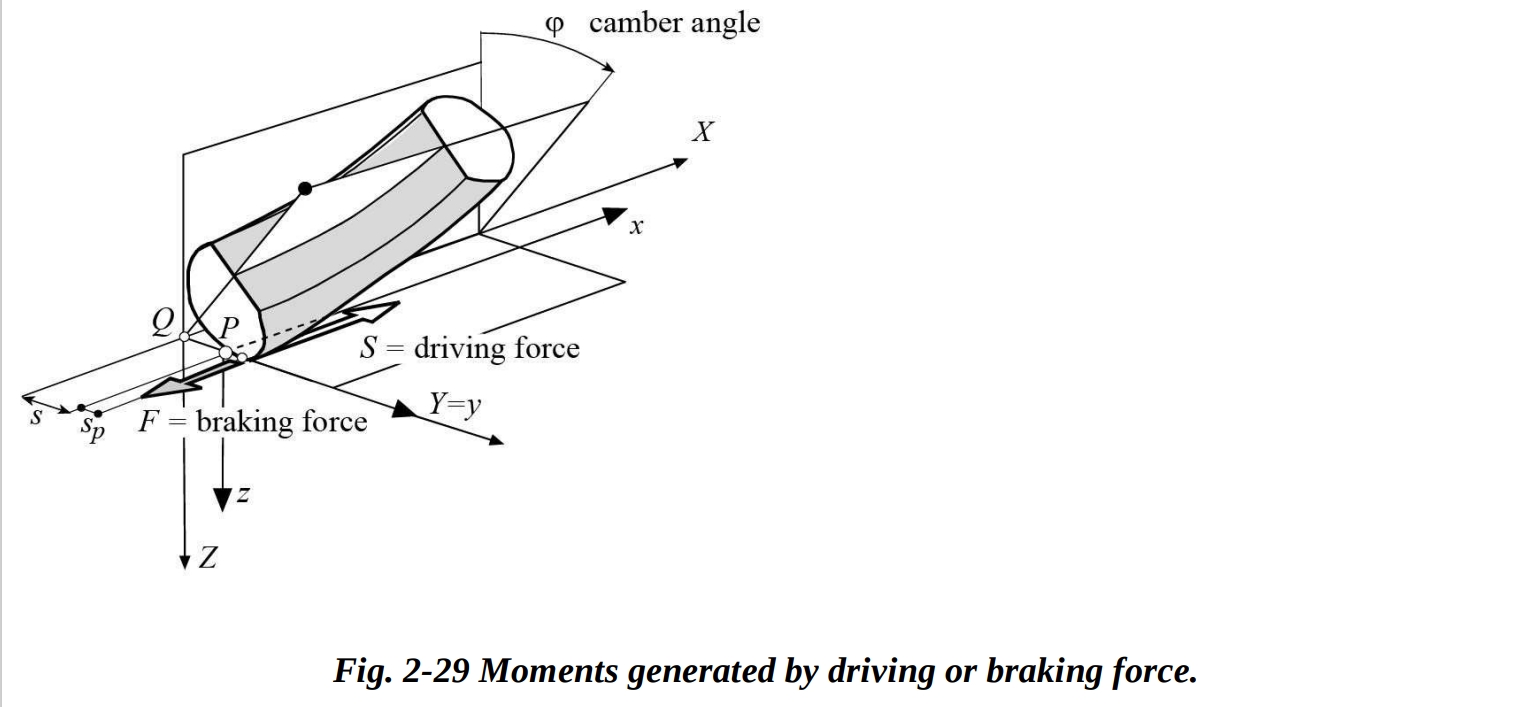
点 $Q$ について、横方向力は、断面の半径とキャンバ角に依存します。ここで、$t$ はタイヤの断面の半径です。

一般的に、横変形 $s_p$ はタイヤの接点の横変位 $s$ に比べて無視できるほ程度の値です。

2.7 横方向と縦方向の力の組み合わせ：摩擦楕円

縦方向の力 $F_x$ は、駆動（$F_x$ の正の値）またはブレーキング（$F_x$ の負の値）のいずれかで、ライダーの制御によって与えられます。

縦方向の力が強まれば、発生可能な横力 $F_y$ は減少します。

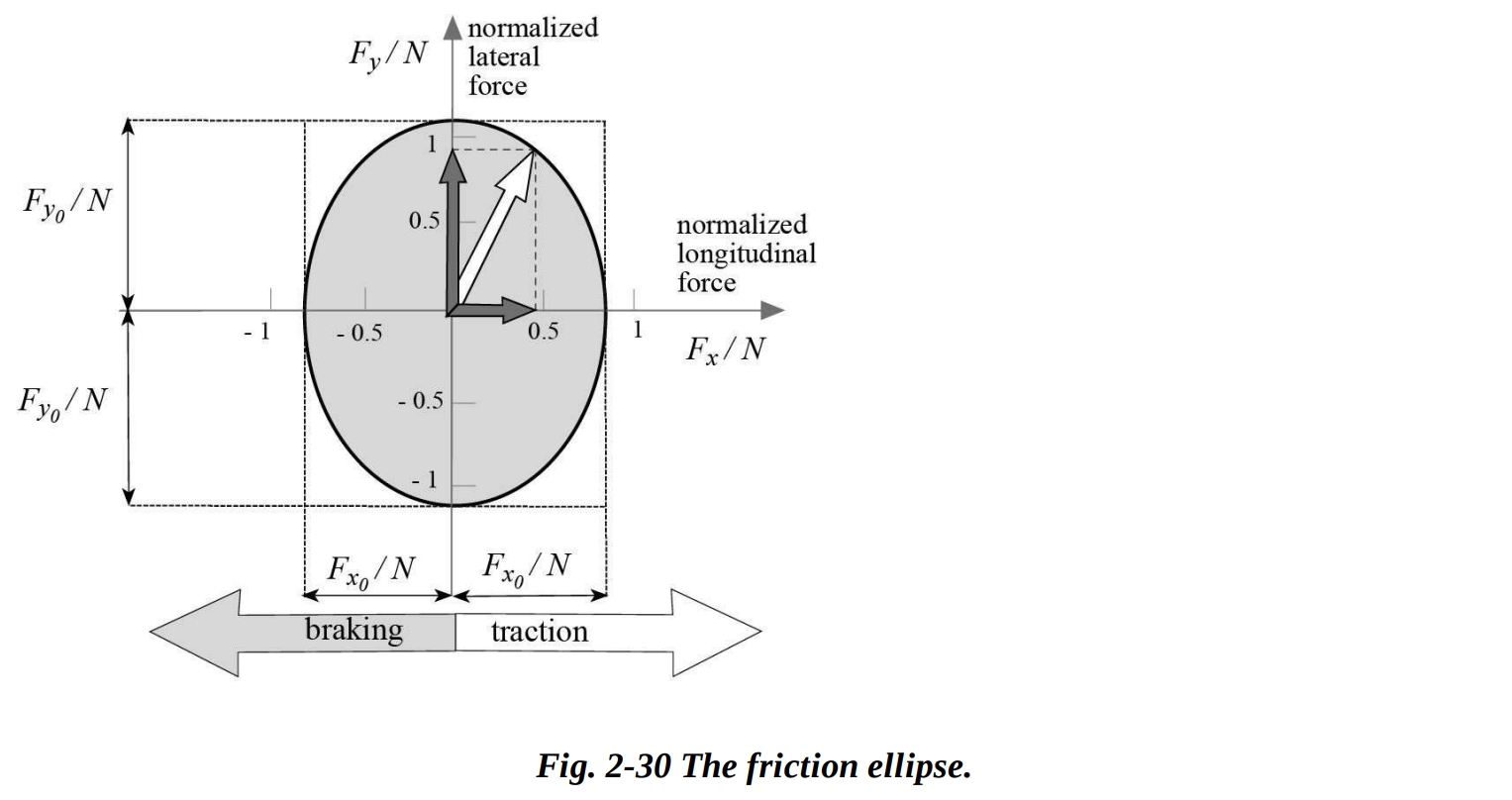
これらの結果は、縦方向と横方向でそれぞれの最大値（$F_{x_0}$ , $F_{y_0}$ ）を持つ摩擦楕円の範囲内になければなりません。

ここで、$\mu_x$ は縦方向のトラクション係数であり、$\mu_y$ は横方向のトラクション係数です。このため、横力を与える式には、縦方向にかかる力に依存する補正係数が乗算されます。

図2-31は、縦方向にかかる力の変化とともに正規化された横力曲線の変化を示しています。

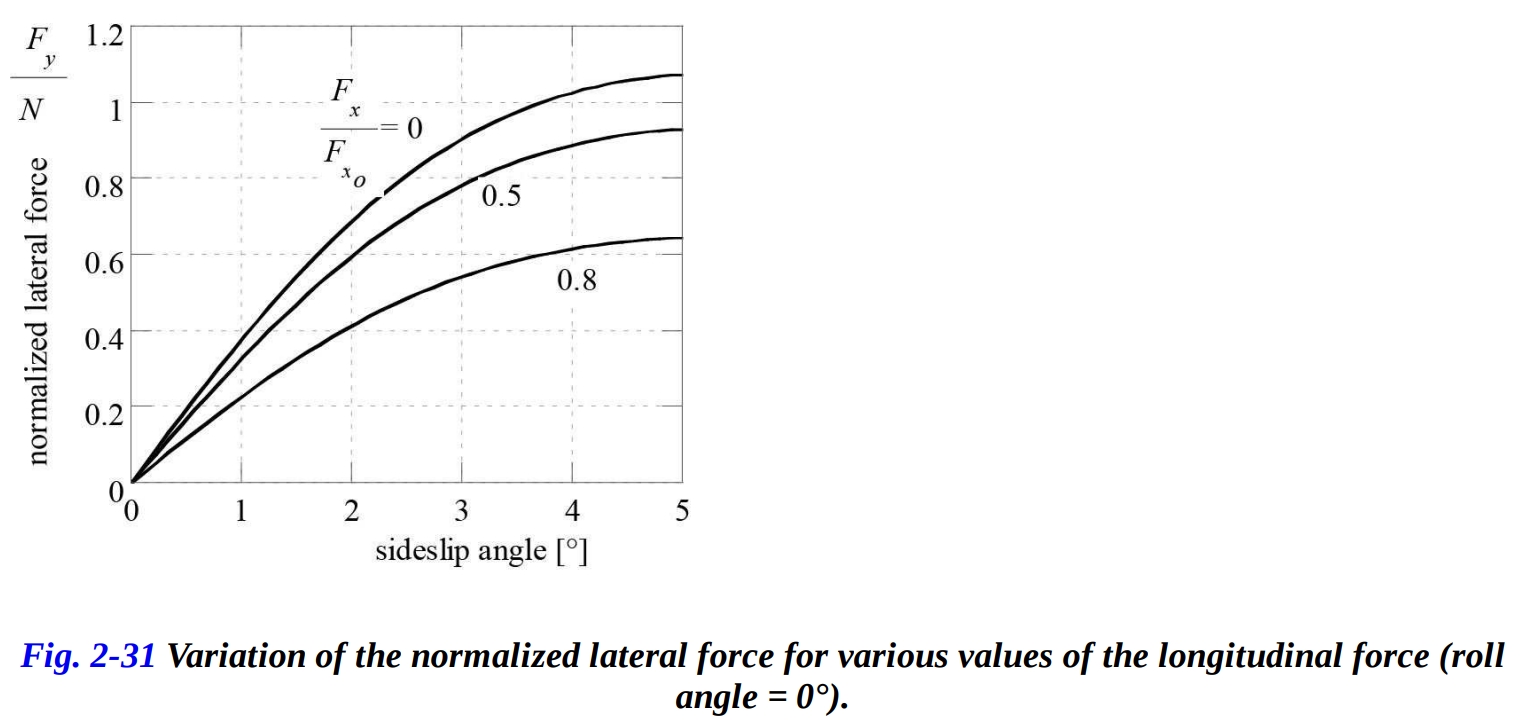
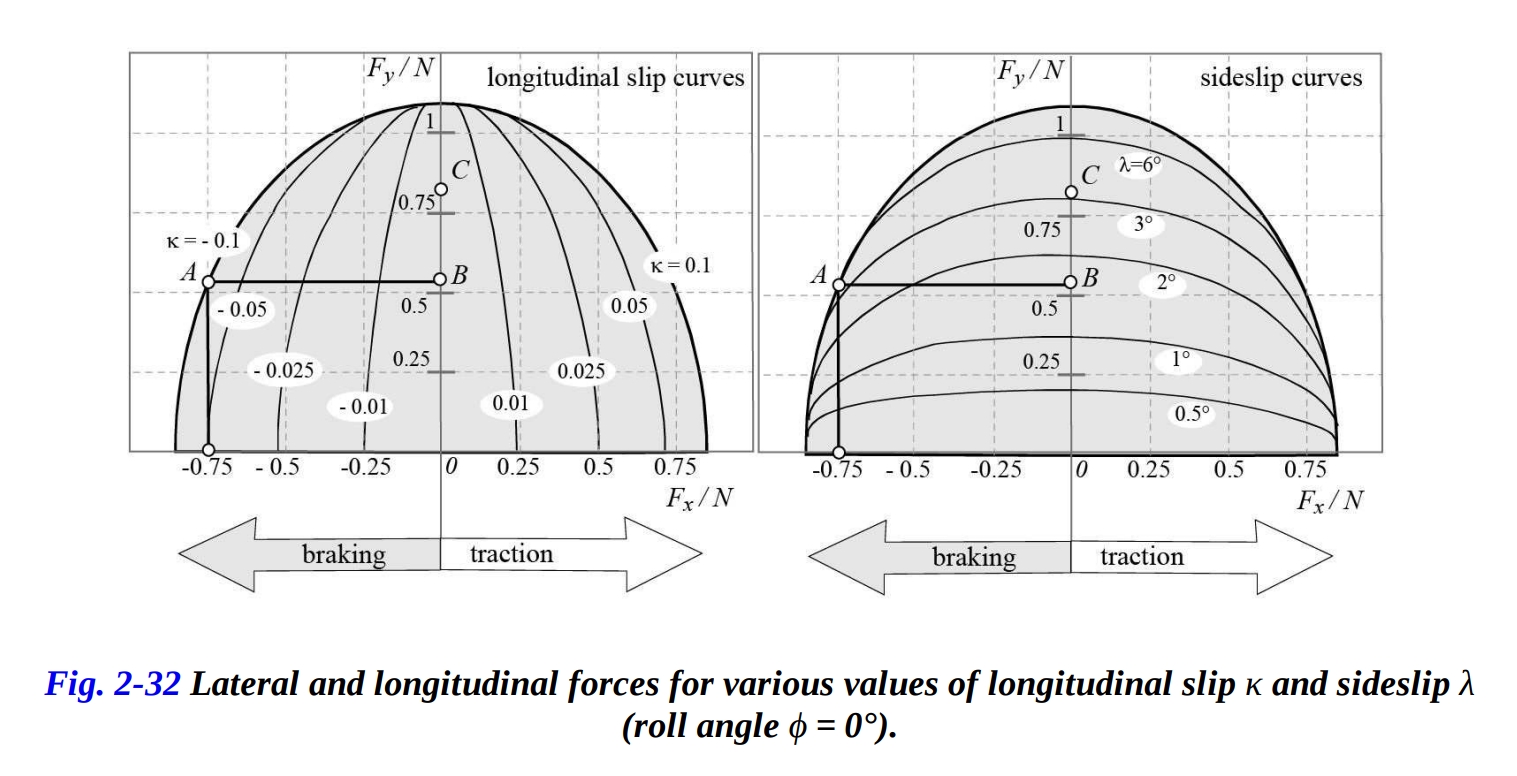
縦方向のスリップと横方向のスリップの相互作用は、定常の横方向のスリップ曲線と定常の縦方向のスリップ曲線を、縦軸に横方向の力 $F_y / N$ 、横軸に縦方向の力 $F_x /N$ のグラフで表されます。定常の縦方向のスリップと定常の横方向のスリップの曲線は、図2-32に示されています。

例3

カーブに入る際にブレーキングしているオートバイを考えます。リアホイールの正規化された縦方向の力が 0.75、正規化された横方向の力が 0.53（点A）であるとします。これは横滑り角が 3.5° に相当します。

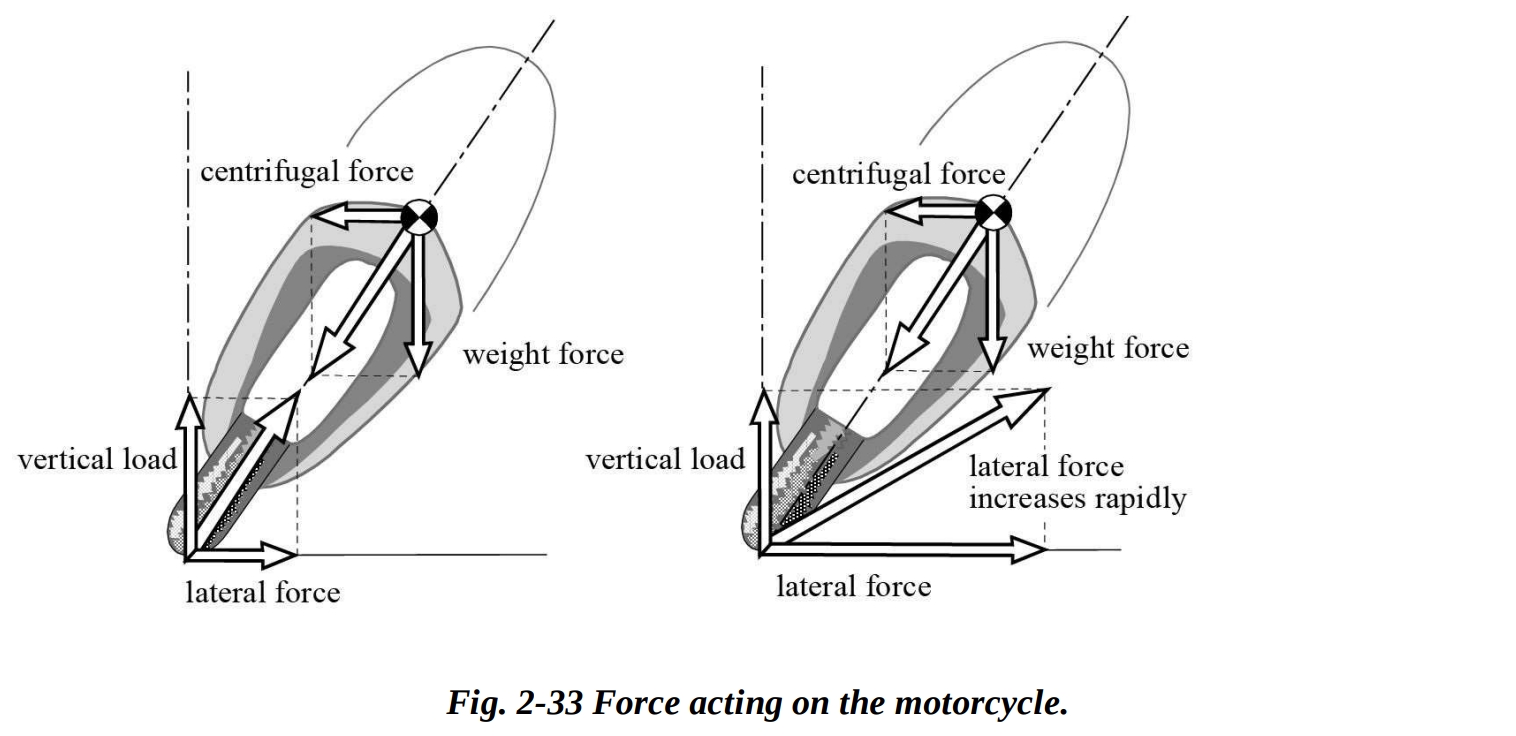
もし急激にブレーキングを止めた場合、3.5°の横滑り角に対応する横方向の力が急激に増加し、点Aから点Cへと移動します。スリップによって生成される横力は今や0.78であり、これは平衡のために必要な0.53よりも大きくなっています。オートバイが傾いているため、横力の急激な増加は、車両を垂直位置に戻そうとする加速度を生成し、ライダーを上方に投射します（ハイサイド転倒）。横滑りは平衡に必要な値に達するまで減少します（点B）。

2.8 カーカスの弾性

タイヤに横方向と鉛直方向の力がかかると、カーカスの横方向および径方向の弾性変形が生じます。さらに、駆動/ブレーキング力は、縦方向の平面で、リムとカーカスの間の相対回転から主に成り立つ変形を生成します。タイヤの変形のため、接触はもはや点状ではなく、キャンバ角、荷重、および空気圧に依存する接触パッチ表面が関与します。 オートバイタイヤの接触パッチの長さと幅は、接触パッチが非常に大きくない限り（大きな荷重）、およびキャンバ角が40°〜45°に近づかない限り、鉛直荷重とキャンバ角と比較的規則的な方法で変化します。接触パッチへの空気圧の影響は、それが名目値2-2.5バールよりも低い場合に重要です。

図2-34に示されているように、道路面ではタイヤの足跡が変化し、接触点がカーカスのジオメトリに応じて横方向に移動します。 キャンバが存在する場合、純粋な鉛直荷重によってカーカスは水平方向および垂直方向に変形します。しかし、結果を車輪のキャンバ角度の基準フレームで表現することにより、力と変形の関係はより単純になります。実際、カーカスの弾性特性は、径方向Zと横方向Yの2つのバネによって効果的に記述できます。これは図2-35に示されています。

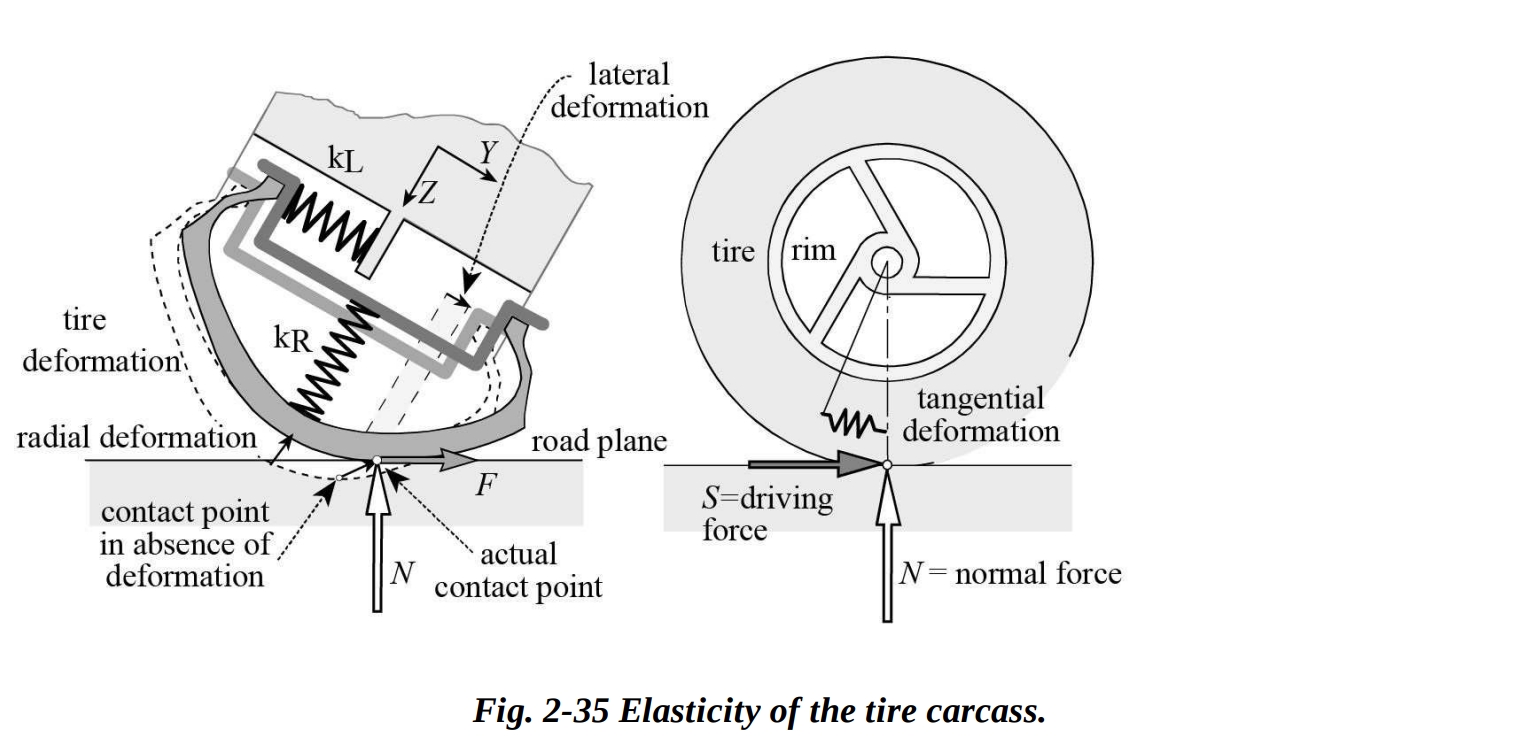
構造的な横方向の剛性の典型的な値は、100 kN/mから250 kN/mの範囲にあります。一方、径方向の剛性は、100 kN/mから200 kN/mの範囲に及びます。

2.9 モーターサイクルタイヤのモデル

現在では、多体動解析コードを使用して、剛性または弾性のトロイダルタイヤを装備したモーターサイクルと道路の接触点を計算することが可能です。したがって、タイヤモデルでは、道路とトロイダルタイヤの接触点周辺の領域に力を作用させることができます。

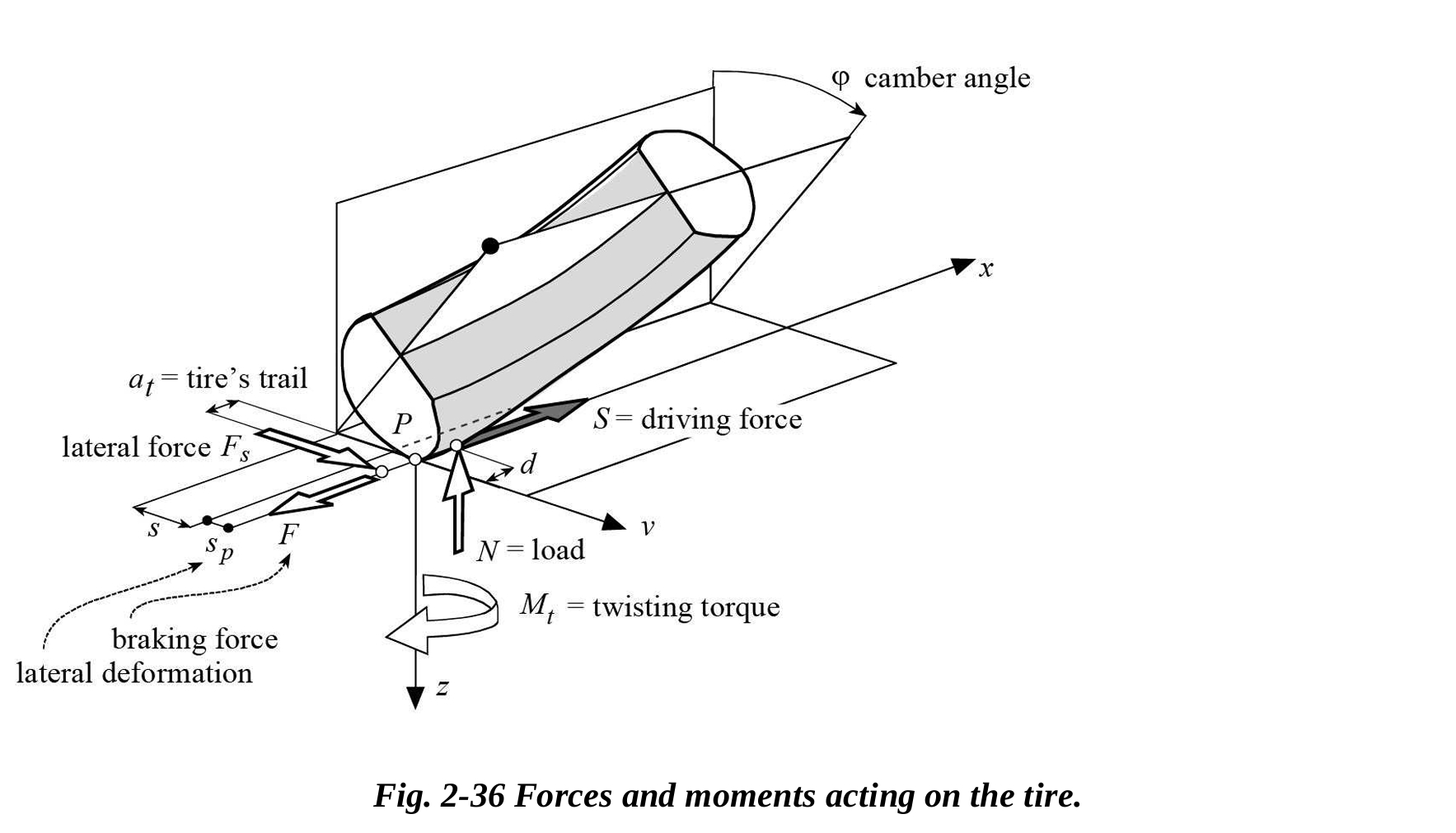
モーターサイクルタイヤのモデルは、タイヤの形状によって定義された理論的接触点付近の点に作用する力を考慮します。 考慮される力は以下の通りです：

垂直抗力 垂直抗力は、理論的接触点の位置に対して距離dだけ前方の点に作用します。この距離dは転がり抵抗係数とタイヤの半径に依存します。

横方向の力 横方向の力は、ホイール平面と道路平面が交差する方向に垂直に作用します。作用点は、理論的接触点に対して後方に距離$a_t$ だけずれています。これはタイヤのトレイルを表し、サイドスリップ角によって変化します。

縦方向の力 の力は、タイヤの横方向の変形性により理論的接触点から横方向にずれた点に作用します。横方向のずれ$s_p$ はタイヤの横方向剛性に依存し、一般的には、ホイールのロール傾斜による幾何学的変位$s$ に比べて無視できるほど小さいです。

x、y、およびz軸周りに作用するモーメントは、上記の力とねじりモーメントによって生成されます。

横転モーメント 横転モーメントMxは、アームが横方向変形spである垂直荷重Nによって生成されます。

転がり抵抗モーメント 転がり抵抗モーメントは、垂直応力の非対称分布によって生成され、垂直荷重が前方に変位します。タイヤの転がり抵抗モーメントは次の通りです。

ヨーイングモーメント ヨーイングモーメントには2つの寄与があります。最初の項は横方向の力によるもので、タイヤの平面を速度の方向に合わせようとします。二つ目の項はキャンバー角が大きくなると増加し、アライメントに逆らって作用します。

図2-37は、仮想プロトタイピングでモデル化されたモーターサイクルタイヤを示しています。タイヤは、一定の速度で道路上に発進し、初期の傾斜した方向を持ち、その軌道はタイヤの特性に依存し、特に以下の点に依存します：

• キャンバーによる横方向の力の成分（キャンバー角の関数）
• タイヤのトレイル（横滑りの関数）
• ねじりモーメント（キャンバー角の関数）

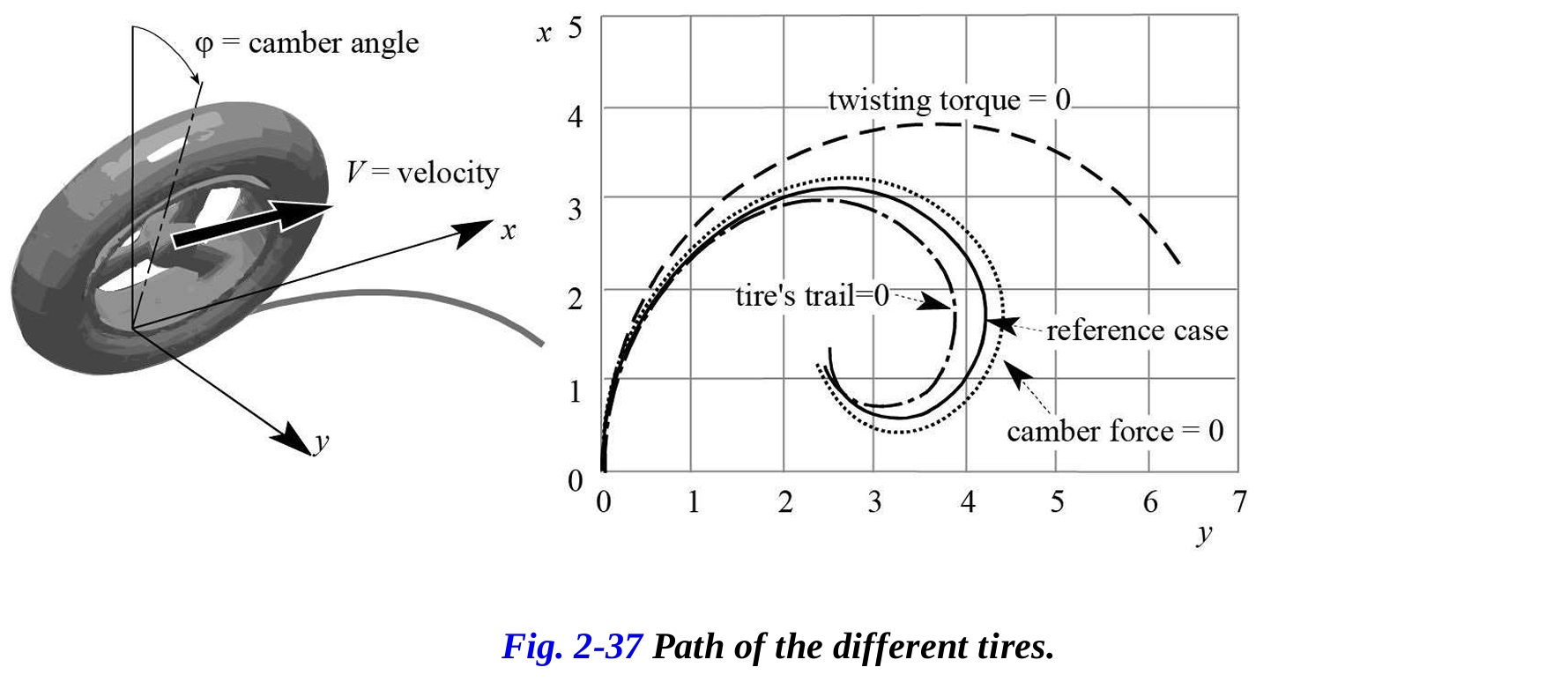
図2-37のグラフは、タイヤによって描かれるさまざまな軌道を示しています。キャンバーによる横方向の力の成分がゼロの場合、横滑りによって生成される成分だけで平衡が確保されます。そのため、横滑りは参照ケースよりも常に大きくなります。横滑りが大きいため、カバーされる軌道は参照ケースの軌道よりも外側になります。タイヤのトレイルがゼロになると、横方向の力によって生成される自己調整モーメントもゼロになります。したがって、描かれる軌道は参照ケースの軌道よりも内側になります。ねじりモーメントはキャンバー角に依存し、タイヤの挙動に大きな影響を与えます。ねじりモーメントの効果はアライメントに逆らうため、すなわちタイヤのヨーを増加させる傾向があるため、ねじりモーメントがゼロになると軌道に大きな変化が生じます。タイヤは、著しく大きな曲率半径を特徴とする経路に沿って移動します。

2.10 タイヤの振動モード

タイヤの動的特性は、モーターサイクルの挙動におけるいくつかの特徴、例えば快適性、衝撃吸収、ブレーキングなどに重要な影響を与えます。これらは面内動力学に関連し、安定性とハンドリングは面外動力学に関連します。

モーターサイクルタイヤの振動モードは、面内モード、面外モード、混合モードに分けられます。面内モードは、ホイールの対称平面に位置する点の半径方向および/または円周方向の変位によって特徴付けられます。面外モードは、ホイールの対称平面に位置する点の横方向の変位が支配的です。混合モードは、半径方向、円周方向、および横方向の変位の組み合わせを示します。

面内モードは、円周波数nの波数に応じて分類されます。$n=0$ モードは円周波数を持たず、呼吸モードと呼ばれます。$n=1$ モードは1つの円周波数を持ち、タイヤトレッドがリムに対して変位することを示します。$n=2$ モードは2つの円周波数を持ち、トレッドが楕円形をしています。

面内モードは最も励起されやすいモードです。定常状態（直線経路）では、タイヤの力の合力（荷重$N$ 、ブレーキ力$F$ 、駆動力$S$ ）はおおよそホイールの対称平面内にあります。ホイールに固定された座標系を考えると、タイヤの力の合力は角速度$\omega=V/R_0$ （ここで$R_0$ はタイヤの転がり半径、$V$ は前進速度）でホイールの周りを回転します。この回転力は、以下の条件が満たされる場合、$n$ 個の円周波数を持つ円周モードを共振条件で励起する可能性があります。

ここで、$v_j$ はモードの固有振動数を表します。

道路の不均一性やタイヤ表面の溝の存在は、高周波数帯域での励起の他の原因です。最後に、ブレーキや車線変更などの過渡操作は、タイヤの力やトルクの急激な変化に対応し、面内モードと面外モードの両方を励起する可能性があります。

一般的に、タイヤの最初の固有振動数は100～200Hzの範囲で、面外モードに対応します。その後、時には混合モードの周波数帯が現れます。周波数が300～400Hz以上になると、面内変位が大きいモードが支配的になります。

自然振動数、損失係数、およびモード形状は、タイヤのサイズ、構造（ラジアル、バイアス）、および材料に強く依存しています。ラジアルとバイアスのモーターサイクルタイヤのモーダル特性を比較すると、ラジアルタイヤの自然振動数がバイアスタイヤよりも高いことがわかります。特に面内モードの場合、この差は大きいです。

地面との接触が存在することで、モードの複雑さが増し、フリー条件で測定されたモードの間には、中間的な形状と周波数を持つ新しいモードが現れます。地面と接触しているモードの自然振動数と損失係数の範囲は、フリー条件で測定されたものとはあまり変わりません。

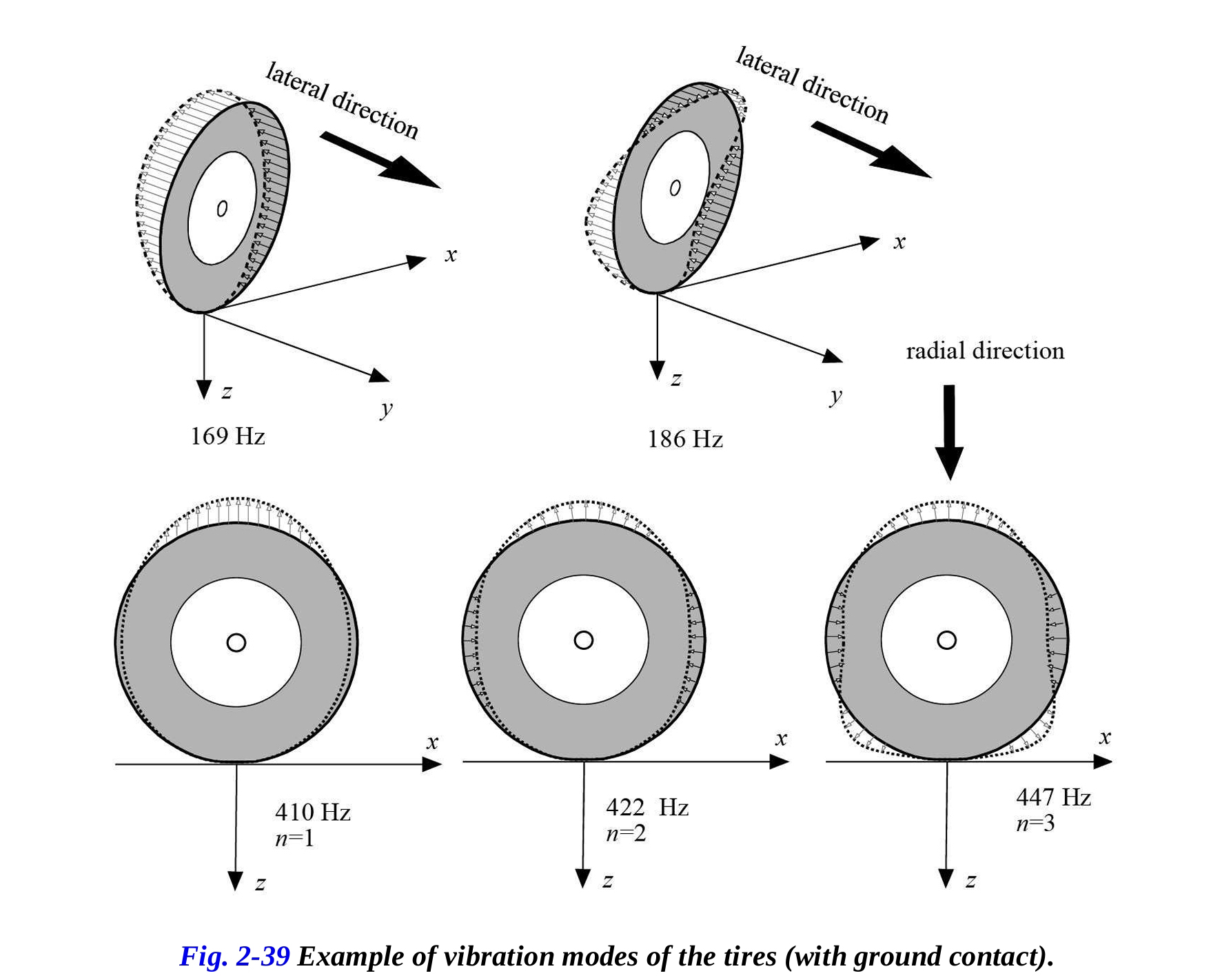
図2-39は、2.2barで空気を充填した120/65 R17のフロントタイヤの自然振動数とモードを示しています。このタイヤは、0°のスチールベルトを持つハイパフォーマンスのラジアルタイヤです。最初の面外モードは、リムに対するタイヤトレッドの横方向の変位です。次に、バナナ形のモードがあります（横方向に1.5波を持ち、他の方向では小さな変位があります）。最初の面内モード（410 Hz）は、主にタイヤトレッドの面内変位であり、フリー条件で測定されたn=1モードから派生しています（接触なし）。

次のモード（422および447 Hz）は、フリー条件で測定された2つの円周波数（n=2）および3つの円周波数（n=3）を持つモードから派生しています。0°スチールベルトの高い円周剛性のため、0-500 Hzの周波数範囲で呼吸モードは特定されません。これらの自然振動数は、自動車タイヤよりも高くなっています。面内モードの損失係数は、自動車タイヤで測定されたものと類似しています。面外モードの損失係数は、タイヤのサイドウォールに主に影響を受けるため、面内モードよりも高くなっています。

3. モーターサイクルの直線運動

モーターサイクルの直線運動の挙動は、タイヤと道路の間で交換される縦方向の力、この運動を通じて生じる空力、および道路面の勾配に依存しています。直線運動の研究は、ブレーキング時のモーターサイクルの挙動（前方転倒の可能性がある）や加速時の挙動（ウィリングの可能性がある）など、安全性にも重要な動的側面を明らかにします。

3.1 モーターサイクルに作用する抵抗力

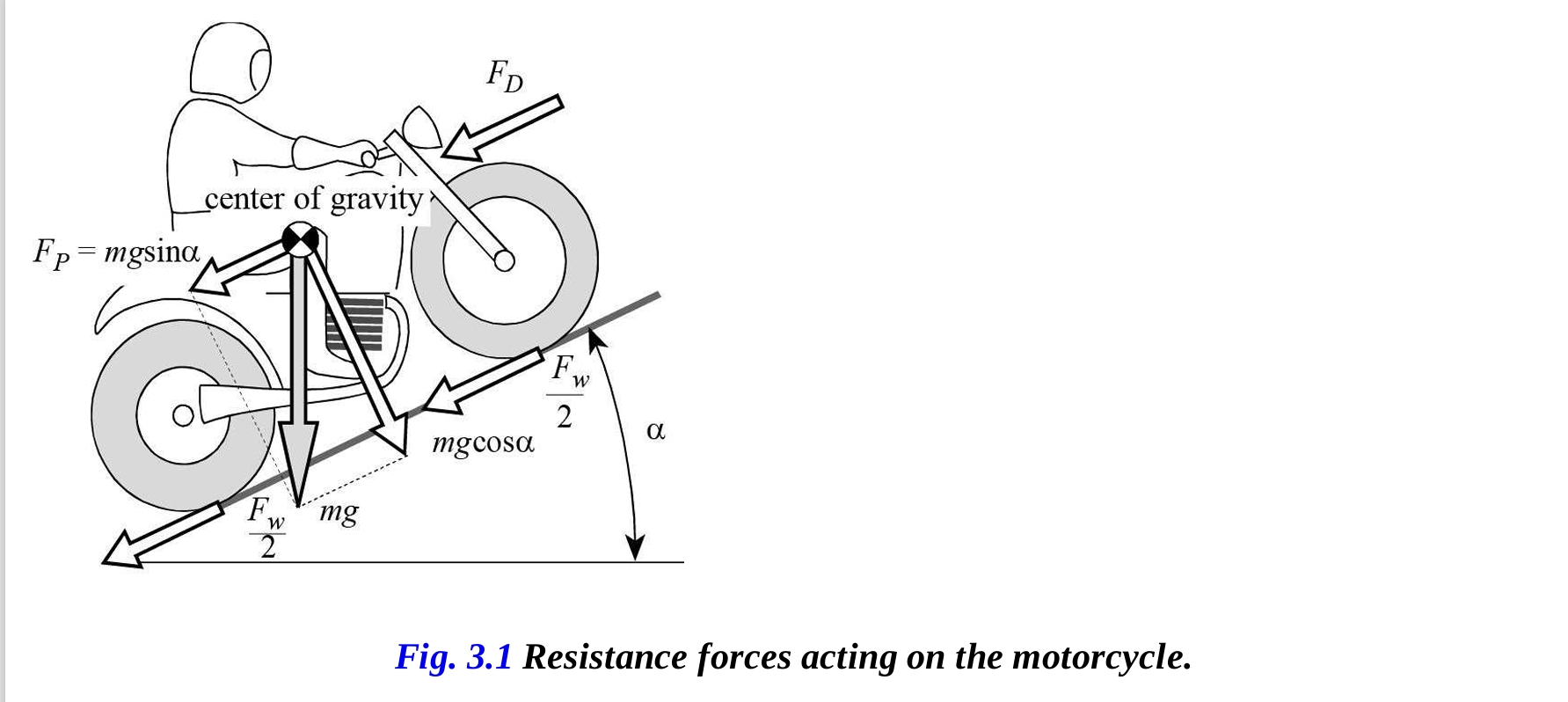
定常状態の運動中、エンジンによって生み出される推力は、前進運動に対抗する力と等しくなり、主に以下の3つの現象に依存します（図3-1）。

• タイヤの転がり抵抗
• 前進運動に対する空気抵抗
• 道路面の勾配によって引き起こされる重力の成分

タイヤの転がり抵抗$F_w$ は、前章で十分に議論されました。一般的に、これは重量の約2%に等しいと考えられます。

3.1.1 空気抵抗力

モーターサイクルに作用するすべての空力影響は、図3-2に示すように、重心に作用すると仮定される3つの力と、重心軸x、y、z周りに作用する3つのモーメントによって表すことができます。

• 前進運動に対抗する抗力
• モーターサイクルを持ち上げるリフト力
• モーターサイクルを横方向に押す横力
• ピッチングモーメント
• ヨーイングモーメント
• ローリングモーメント

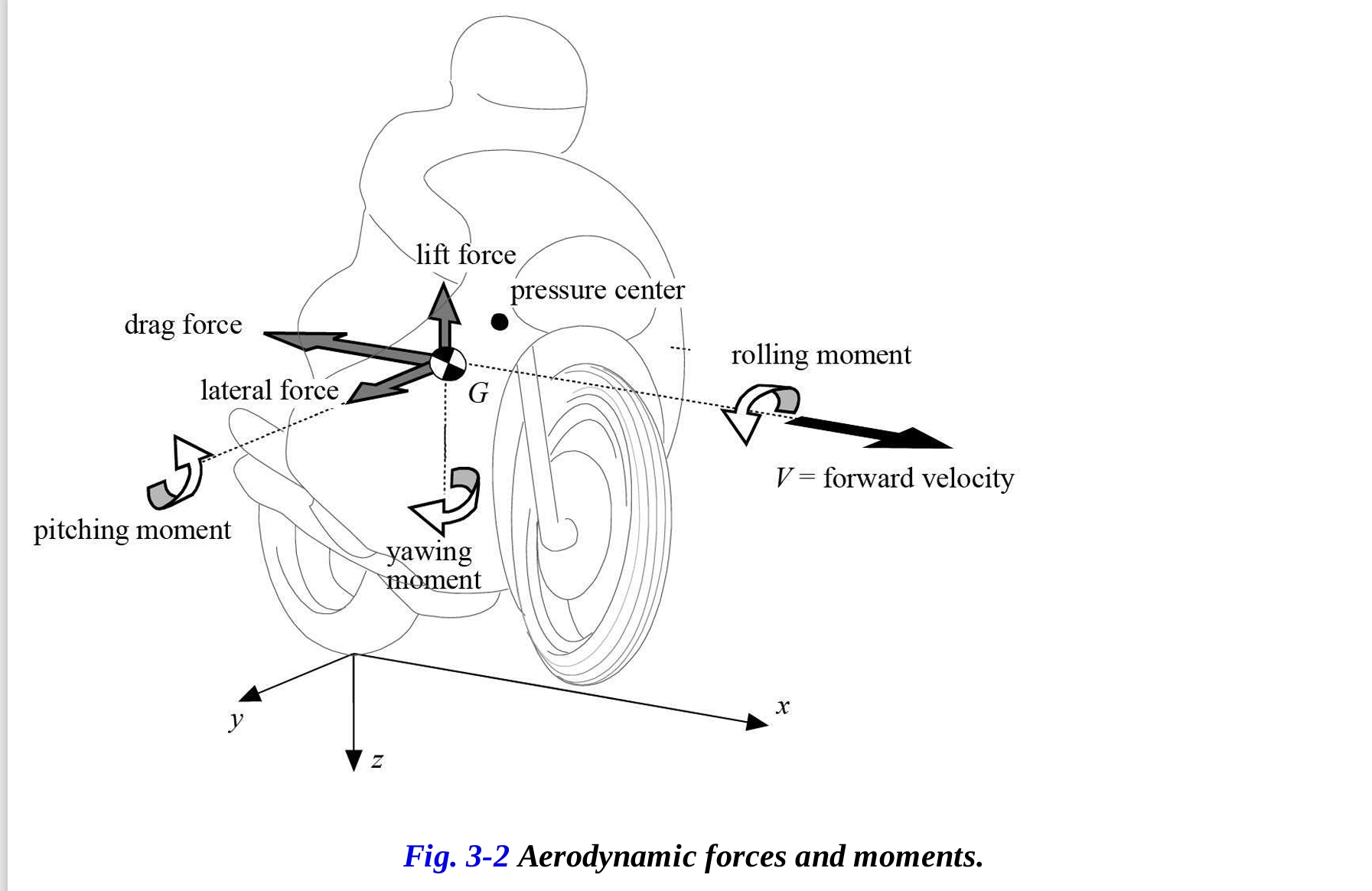
最も重要な成分は抗力とリフト力です。これらは圧力中心と呼ばれる点に作用し、圧力中心は重心と一致せず、一般的に重心の上に位置しています。したがって、これら2つの空力力の合力は、y軸周りにピッチングモーメントを生成します。

抗力は、最大到達速度と加速性能の両方に影響を与えます。抗力 $F_D$ は、モーターサイクルの前進速度の二乗にほぼ比例します。

• $\rho$ 空気密度を表し、987 mbar の気圧および 20°C の温度で 1.167 kg/m³
• $A$ モーターサイクルの前面投影面積
• $C_D$ 空気抵抗係数（抗力係数）
• $V$ モーターサイクルの前進速度

係数 $C_D$ の値は、特にフェアリング（カウル）の有無によって、モーターサイクルの形状に強く影響されます。一般的に、渦の後流が形成され、境界層がフェアリングの表面から剥離すると、空気抵抗が大幅に増加します。

モーターサイクルと空気の相互作用は、速度の二乗に比例する揚力 $F_L$ も発生し、これにより前輪および場合によっては後輪の荷重が減少します。

ここで、$C_L$ は揚力係数です。

モーターサイクルの揚力は危険であり、これはタイヤの荷重を減少させ、タイヤの接地性を低下させます。特に前輪に関しては、圧力中心が一般的に重心の前方かつ上方にあるため、この問題が顕著です。典型的なモーターサイクルは正の（上向きの）揚力を生成しますが、この現象に対抗し、タイヤの荷重を増加させるためには、レーシングカーのように前部にウィングを取り付ける必要があります。現代のフェアリングは、望ましくない揚力効果を最小限に抑えるよう設計されています。

モーターサイクルの空力特性は、抗力面積 $C_D A$ （抗力係数と前面投影面積の積）と揚力面積 $C_L A$ 揚力係数と前面投影面積の積）によって決まります。抗力面積 $C_D A$ の値は、完全にフェアリングされた速度記録用では0.18 m²から、フェアリングがなくライダーが直立した位置にあるモーターサイクルでは0.7 m²まで変わります。典型的な「スーパーバイク」では0.30から0.35 m²、「グランプリ」モーターサイクルでは0.22 m²以下の値になります。小型の前部フェアリングを持つツーリングまたはスポーツモーターサイクルでは0.4から0.5 m²の値を持ちます。直立姿勢から伏せた姿勢への変化は、モーターサイクルの種類やライダーの体格に応じて、5から20%の$C_D A$ の値の減少をもたらします。

モーターサイクルの各コンポーネントは、前進抵抗に様々な影響を与えます。例えば、以下は$C_D A$ の値に影響する要素 です。

• 前部フェアリングは0.02から0.08 m²の改善をもたらします。
• サイドフェアリングは約0.15 m² $C_D A$ を減少させます。
• サイドミラーは0.012から0.025 m² 抗力面積を増加させます。
• 後部フェアリングの存在は0.015 m² 改善します。
• 適切に設計されたサドルバッグは0.02 m² 改善します。
• 下部スポイラーは0.01から0.02 m² の範囲で改善します。

前面投影面積 $A$ はモーターサイクルの種類によって異なり、ライダーの体格や走行中の姿勢に強く影響されます。参考値は、大排気量ツーリングモーターサイクルで0.6から0.9 m²、スポーツモデルで0.4から0.6 m²、グランプリモーターサイクルで0.4から0.5 m²の範囲です。小排気量グランプリクラスモーターサイクル（125cc）は約0.32 m²の値に達します。前面投影面積$A$ と$C_D A$ の値が分かれば、通常0.4から0.5の範囲である抗力係数$C_D$ を評価することができます。揚力係数と断面の前面投影面積の積である$C_L A$ の値は0.06から0.12 m²の範囲です。

前述の力によって生じるピッチングモーメントは危険であり、前輪の荷重が減少し、後輪の荷重が増加します。これらの変化はモーターサイクルの動的挙動に大きな影響を与える可能性があります。

直線運動中に横風がない場合、ライダーを含むモーターサイクルのx-z平面が対称平面となり、モーターサイクルの前進速度はその平面内にあります。このとき、横方向の空力力およびロールおよびヨーイングモーメントはゼロです。しかし、ライダーが対称位置から移動した場合、横風がある場合、またはタイヤの横滑り角がゼロでない場合、これらはゼロではありません。特に、ライダーがカーブに入るとき、体や膝をカーブの内側に移動させると、空力的なヨーイングモーメントが発生し、モーターサイクルがカーブに入るのを助けます。カーブ中にライダーがこの傾斜した位置に留まると、横方向の空力力が持続します。

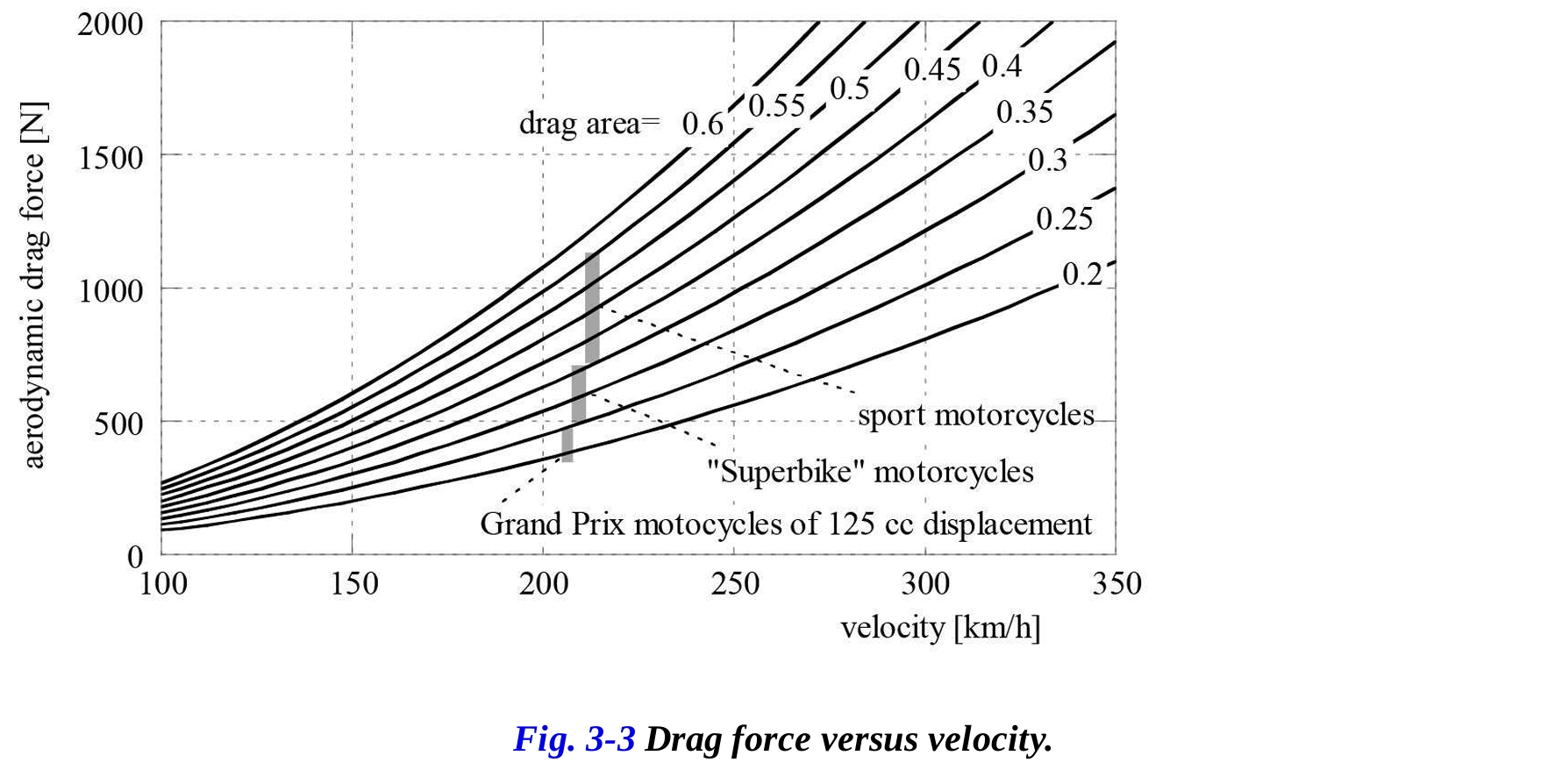
空力力によって消費されるパワーは速度の3乗に依存するため、高速を達成するには多くのパワーが必要です。図3-3は、さまざまな抗力面積の値に対する速度に対する抗力の変動を示しています。

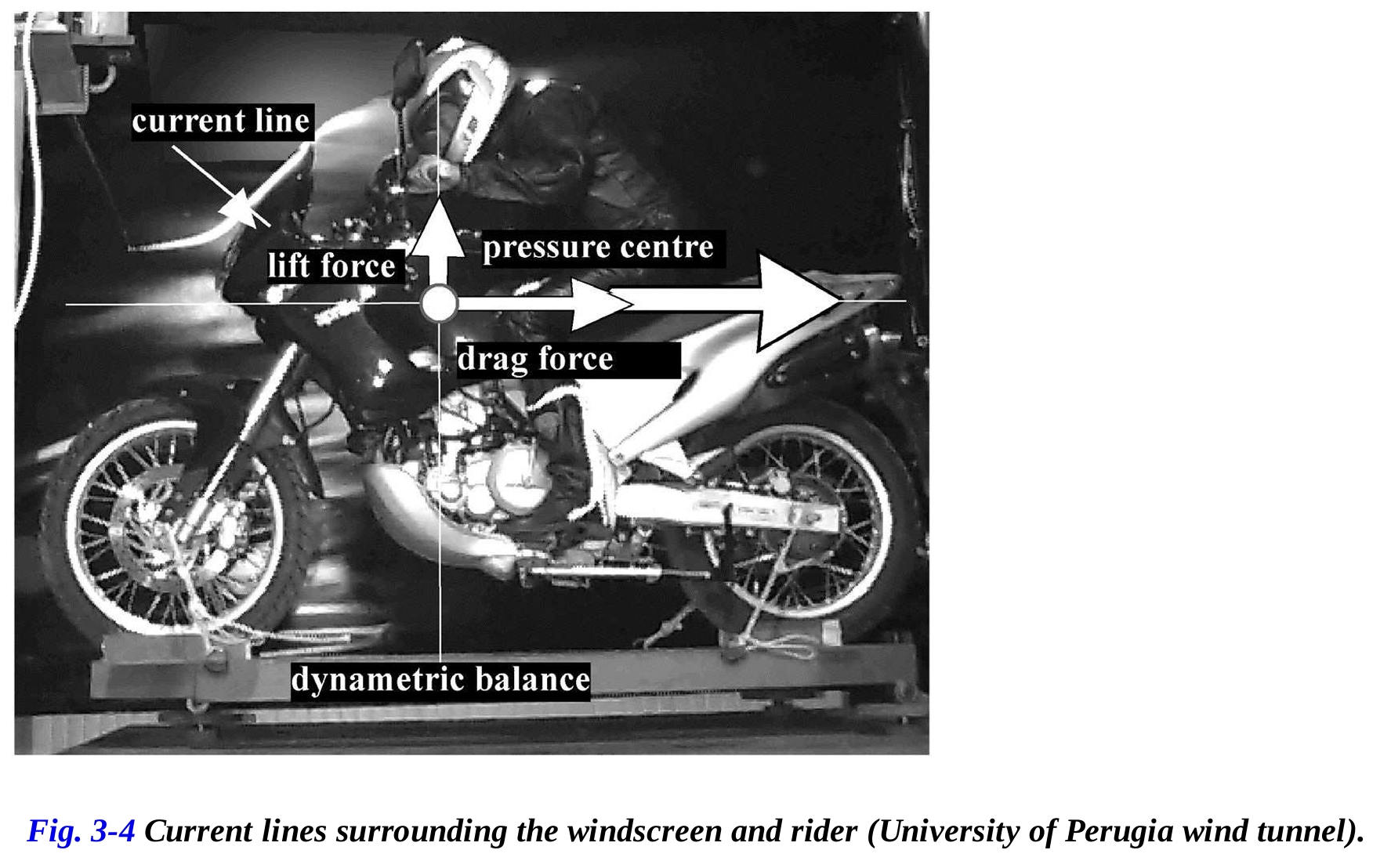
これらの力と空力モーメントは、モーターサイクルを力のバランスに取り付けた風洞実験で測定できます。風洞実験により、渦の存在やモーターサイクル周囲の流線を特定することができます。煙を使用して流線を可視化することができ、図3-4に示すように見ることができます。

風洞が利用できない場合、抗力面積 $C_D A$ を次の方法で求めることができます。モーターサイクルを直線道路で最高速度まで走らせ、エンジンのRPM（回転数）と最高速度を記録します。測定された回転数に対応するパワーはダイナモメータ曲線で求められます。抗力係数と前面投影面積の積$C_D A$ は次のようになります。

転がり抵抗を考慮せずに。最高速度が正確に測定されていない場合や、モーターサイクルの実際のパワーが計算に使用されたダイナモメータ曲線と一致しない場合には、重大な誤差が生じる可能性があります。

第二のアプローチは次の通りです。モーターサイクルを一定速度で平坦な道路上で走らせ、その後ニュートラルにします。モーターサイクルが初速度$V_{initial}$ から低速$V_{end}$ に減速するのに要する時間$\Delta t$ を測定し、抗力面積は次のように求められます。

一定速度でアイドリングするのは操作上の困難が伴うことがあります。さらに、質量$m$ には回転慣性も考慮する必要があります。

例1：

スポーツバイク（$C_D A = 0.35$ ）を250 km/hおよび275 km/hの速度に押し上げるために必要なパワーを、転がり抵抗力と抗力の両方を考慮して計算します。 最大速度250 km/hでのホイール上のパワーは71.1 kWです。最大速度を10％（275 km/h）増加させるためには、32％のパワー増加（94.0 kW）が必要です。

3.1.2　道路の傾斜によって生じる抵抗力

道路面の傾斜によって生じる抵抗力$F_P$ は、バイクの進行方向における重力の成分に等しくなります。

ここで、$\alpha$ は道路面の傾斜角度を表します。

図3-5は、さまざまなパワーレベルに対するホイール上の速度と道路傾斜の曲線を示しています。

例 2：

次の特性を持つバイクを考えます。

以下に与えられた条件の下で速度を維持するために必要な推進力と動力を計算してみましょう。

ケース 1: 平坦な道路で時速200kmで走行

平坦な道路 ($\alpha = 0$ ) で時速200km (55.6 m/s) の速度を維持するために必要な駆動力は、空気抵抗力($F_D$ ) と転がり抵抗力($F_w$ )の合計に等しくなければなりません。

空気抵抗力:

与えられた値:

計算:

この推進力の値の場合、ホイールでの動力（P）は以下のとおりです。

ケース2：時速200kmの上り坂

オートバイが同じ速度で走行する場合でも、道路の傾斜が12%（角度α = 6.84°）の一定の坂道を走行する場合は、道路面の傾斜によって生じる抵抗力も考慮する必要があります。

道路の傾斜によって生じる抵抗力:

この場合、必要な推進力は次の通りです:

この推進力の値の場合、ホイールでの動力 (P) は次の通りです:

3.2 重心と慣性モーメント

3.2.1 オートバイの重心

オートバイの重心の位置は、オートバイの動的挙動に大きな影響を与えます。その位置は、オートバイの各部品（エンジン、タンク、バッテリー、排気管、ラジエーター、ホイール、フォーク、フレームなど）の質量の分布と量に依存します。エンジンは最も重い部品であり（総質量の約25%）、その位置がオートバイの重心の位置に大きな影響を与えます。

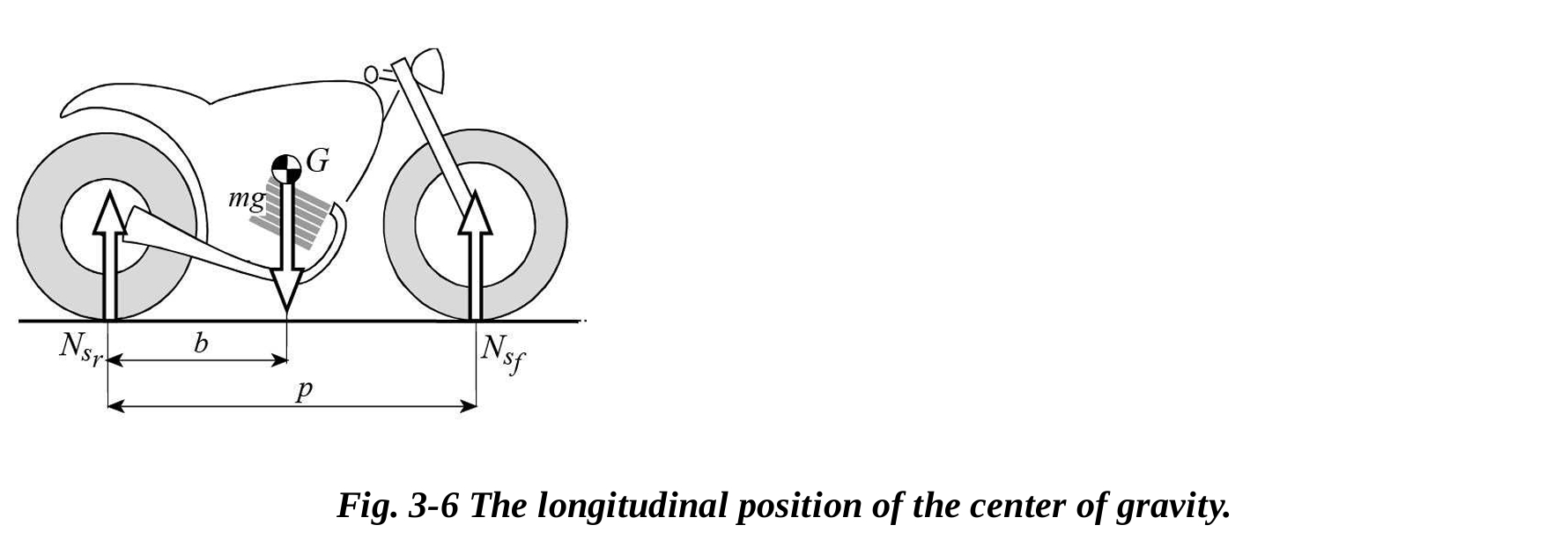
後輪の接地点と重心の間の縦方向の距離 b は、静的状態でのオートバイの総質量およびホイールにかかる荷重（前輪荷重$N_{s_f}$ 、後輪荷重$N_{s_r}$ ）を測定することで簡単に求めることができます。

一般的に、オートバイは車輪にかかる静的荷重で特徴付けられ、以下のような割合の式で表されます。

重心が前方にある場合（前輪荷重が50%以上）、オートバイをホイリングすることがより難しくなり、つまり地面へのパワーの伝達が容易になります。これはレーシングバイクが前部に重荷を置く理由の一つです。さらに、前部に大きな荷重をかけることで、空力による前輪のアンロードを補償するので、高速走行時に重要な要素となります。一方、重心がオートバイの後方に位置すると、ブレーキング能力が向上し、特に急激な前輪ブレーキ操作による「ストッピー」や前方に転倒する危険が減少します。

現代のスポーツバイクは、加速とブレーキングの両方で優れたパフォーマンスを発揮するために、前後の荷重配分を50％ずつに保つ傾向があります。安全性の観点から考えると、加速フェーズで後輪の縦滑りが生じるのは前輪の縦滑りよりも好ましいことです。ライダーがいない場合の前後の荷重比率 b/p は、スクーターで最小値が0.35、レーシングバイクで最大値が0.51の範囲で変動します。

一般的に、ライダーの位置は全体の重心を後方に移動させます（図3-7参照）。そのため、ライダーの存在は後輪に荷重を増加させ、それにより前輪への荷重の割合が減少します（例えば、前後の荷重比率 b/p が0.53から0.50に変化する）。

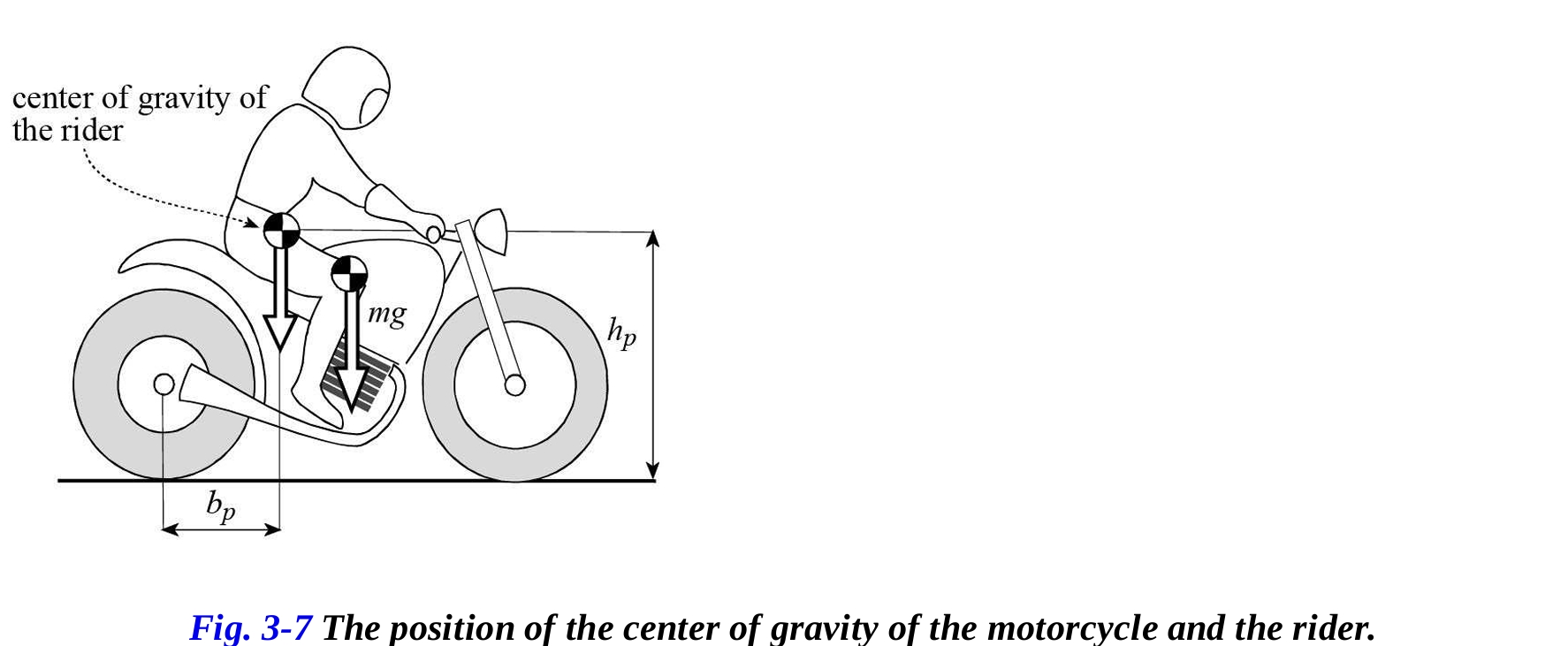
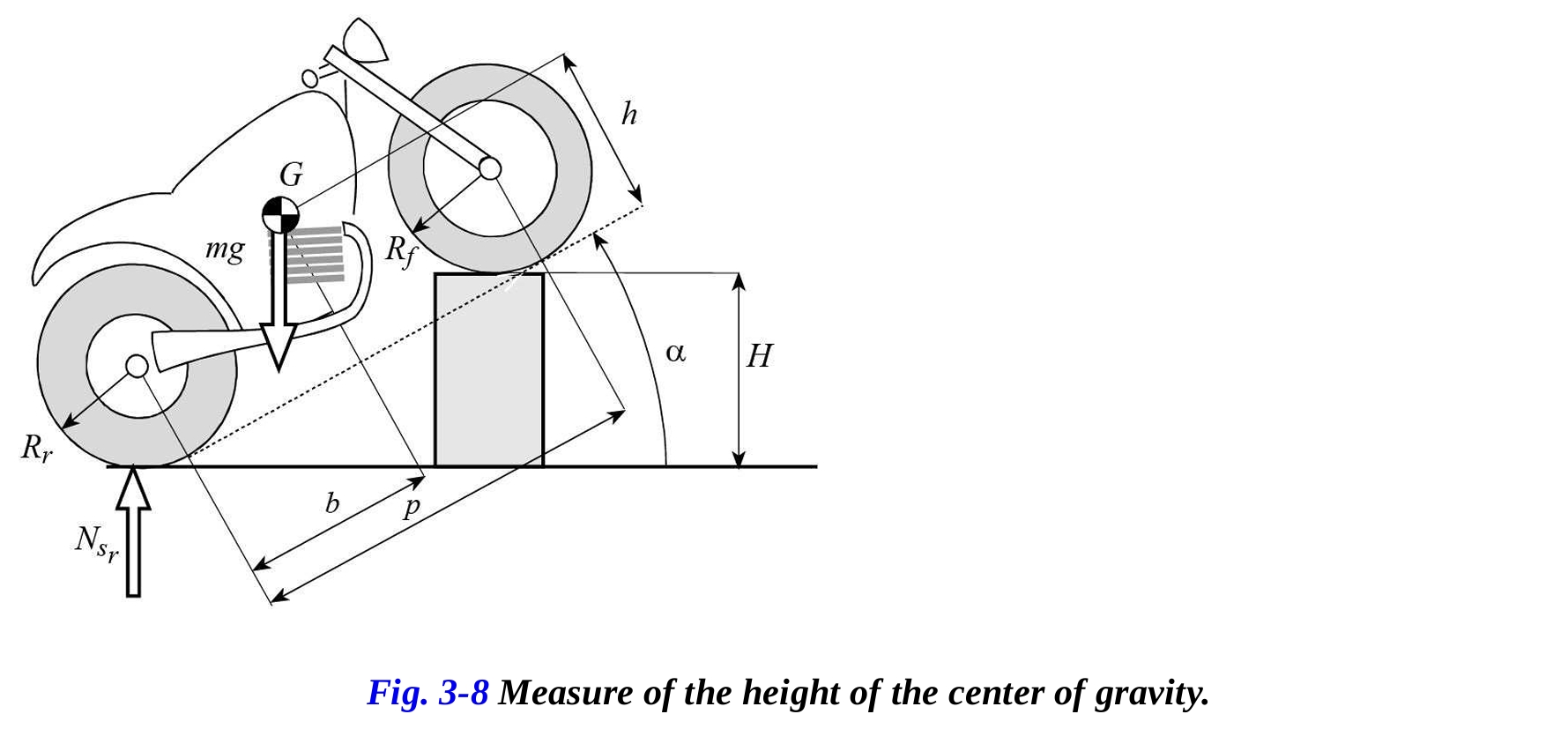
重心の縦方向の位置が分かれば、その高さは図3-8のように、前輪を既知の高さまで持ち上げて後輪にかかる荷重を測定することで決定できます。

重心の高さは、特に加速およびブレーキングフェーズにおいてオートバイの動的挙動に大きな影響を与えます。加速フェーズでは、高い重心は前輪から後輪への荷重移動を大きくし、後輪にかかる荷重が増えることで地面に適用できる駆動力が増加しますが、前輪への荷重が減少するためホイリングが起こりやすくなります。

ブレーキング時には、高い重心は前輪への荷重を増加させ、後輪への荷重を減少させます。前輪への荷重が増加するとブレーキング性能は向上しますが、後輪が完全にアンロードされることで前方への転倒（ストッピー）が発生しやすくなります。

重心の最適な高さは、タイヤと路面の間の駆動／ブレーキングトラクション係数にも依存します。駆動／ブレーキングトラクション係数が低い場合（道路が濡れている、または汚れている時）、加速およびブレーキング能力を向上させるために重心が高い方が良いです。駆動／ブレーキングトラクション係数が高い場合には、ホイリングや前方への転倒の限界状態を避けるために重心が低い方が良いです。

重心の高さとその縦方向の位置の選択は、オートバイの用途とパワーを考慮した妥協点であることは明らかです。全地形対応バイクは比較的高い重心で特徴付けられ、非常に強力なバイクは通常、低い重心を持っています。重心の位置の主な影響は次の図にまとめることができます。

前方の重心	オートバイはオーバーステアする傾向がある（カーブで後輪が横方向に大きく滑る）
後方の重心	オートバイはアンダーステアする傾向がある（カーブで前輪が横方向に大きく滑る）
高い重心	加速時に前輪が浮きやすくなる。ブレーキング時に後輪が浮きやすくなる
低い重心	加速時に後輪が滑りやすくなる。ブレーキング時に前輪が滑りやすくなる

オートバイ単体の重心の高さは0.4〜0.55mの範囲で変動しますが、ライダーが乗ることで重心が0.5〜0.7mに上がります。もちろん、重心の移動はライダーの質量とオートバイの質量の関係に依存します。

ライダーがいない状態でサスペンションが完全に伸びた状態では、重心の高さとホイールベースの比率 (h/p) は0.3〜0.4の範囲で変動します。最小値はクルーザーやスクーターに、最大値はデュアルスポーツやエンデューロタイプのオートバイに見られます。

例3

質量196kgのオートバイが、前後50%の静的重量分布と1390mmのホイールベースを持っています。77kgのライダーが後輪の中心から600mmの位置に重心を持っています。このライダーが乗ることで全体の重量分布はどのように変わるでしょうか。

ライダーが乗ることで、後輪への荷重の割合は52%に増加し、前輪への荷重の割合は48%に減少します。

3.2.2 慣性モーメント

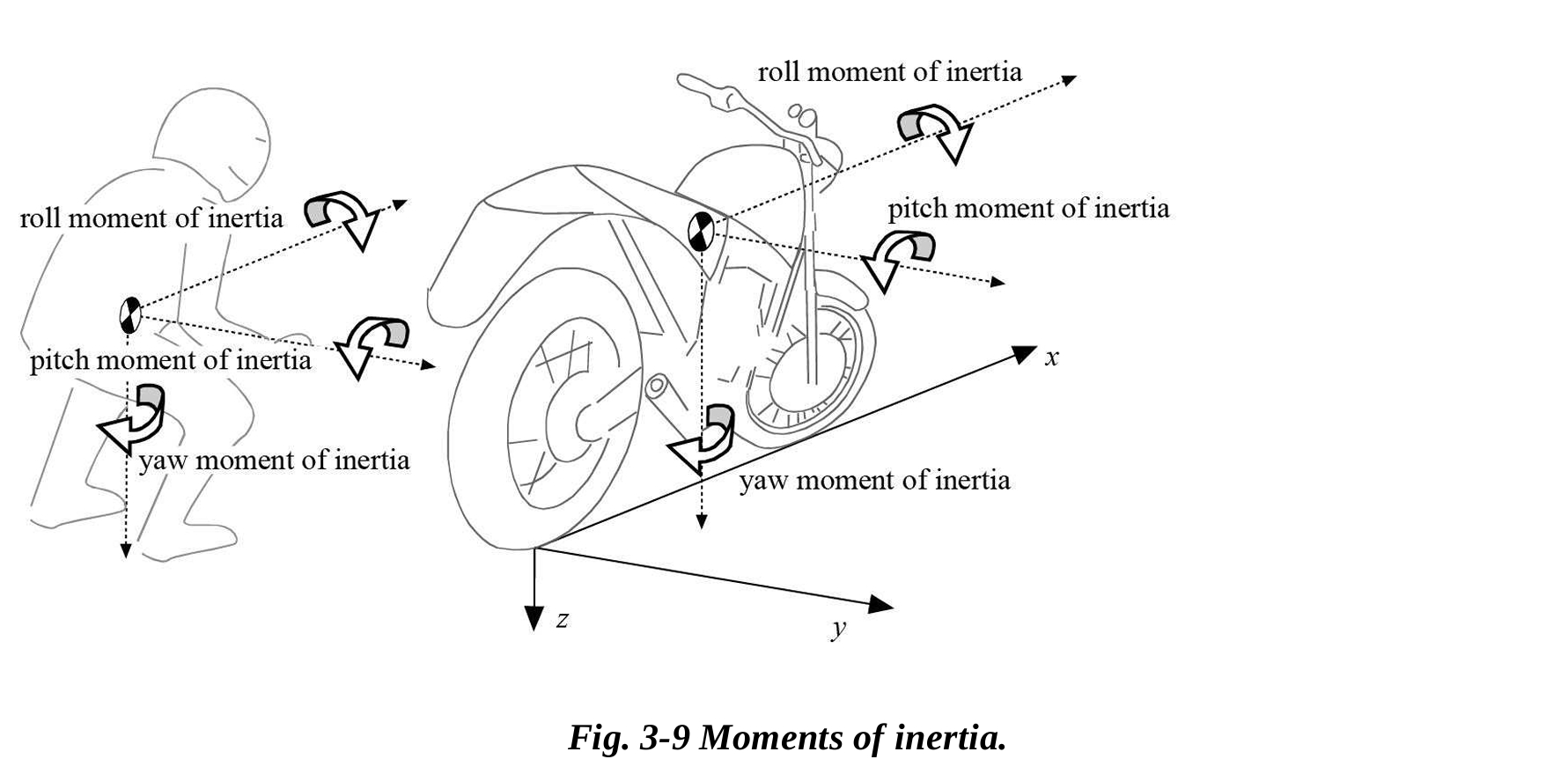
オートバイの動的挙動は、オートバイとライダーの慣性にも依存します。慣性モーメントの測定は複雑な同定手法に基づいており、本書の目的を超えています。最も重要な慣性モーメントには、メインフレームのローリング、ピッチング、ヨーイングの慣性モーメント、ステアリング軸に対するフロントフレームの慣性モーメント、ホイールの慣性モーメント、エンジンの慣性モーメントがあります。以下の表に、重心に対するオートバイとライダーの回転半径の値が示されています（慣性モーメントは、質量と回転半径の二乗の積で表されます）。

ヨーイング慣性モーメントはオートバイの操縦性に影響を与えます。特に、重い荷物を荷台に載せた場合など、高いヨーイング慣性モーメントは操作性を低下させます。ローリング慣性モーメントは、オートバイのローリング運動の速度に影響を与えます。同じ重心の高さを維持したまま、ローリング慣性モーメントが高いと、カーブの入り口と出口の両方でローリング運動が遅くなります。

	ロール回転半径[m]	ピッチ回転半径[m]	ヨー回転半径[m]
Motorcycle	0.18 - 0.28	0.45 to 0.55	0.41 to 0.52
Rider	0.23 to 0.28	0.23 to 0.28	0.15 to 0.19

3.3 オートバイの定常直線運動における平衡

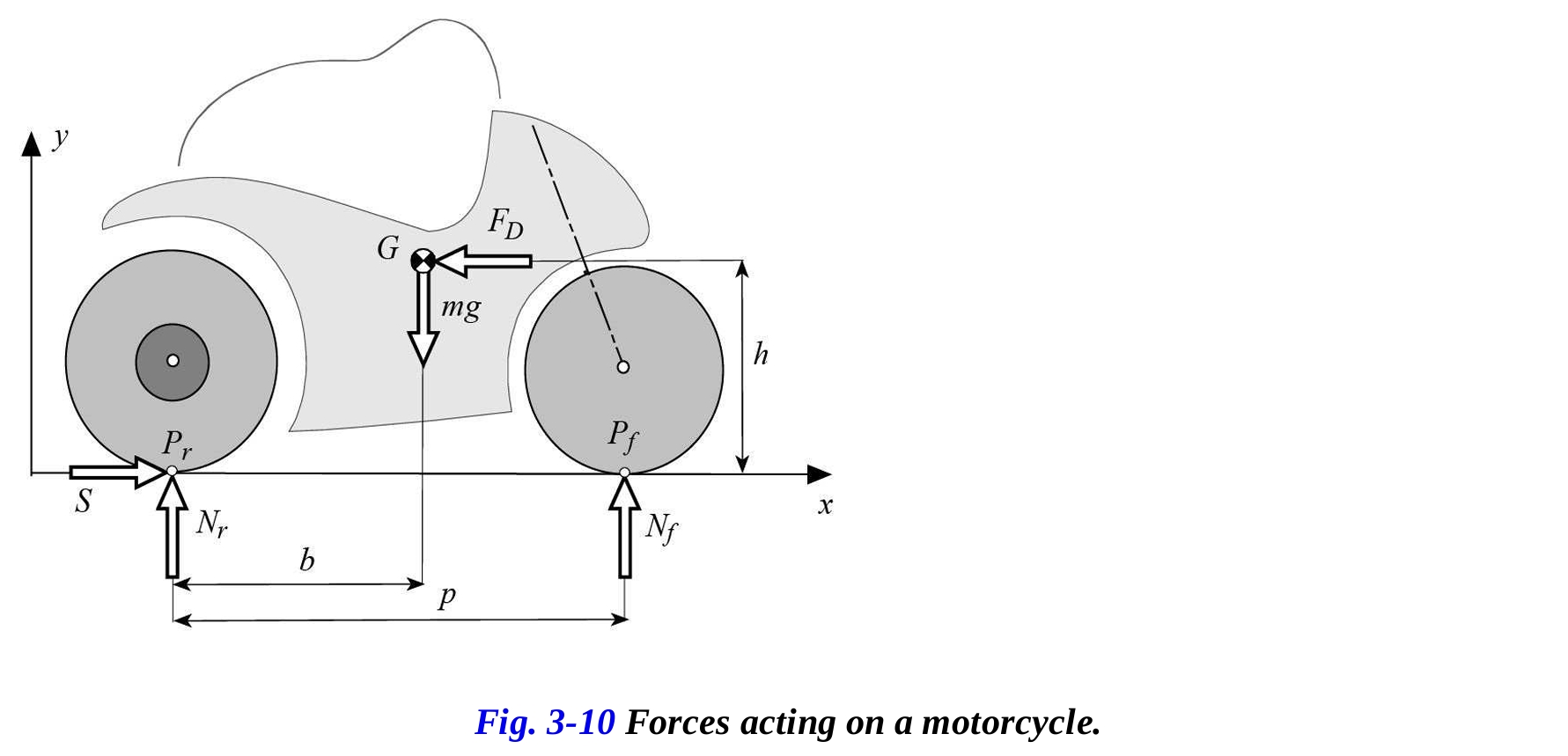
図3-10に示されるオートバイとライダーのシステムモデルに関して、以下の3つの仮説を導入します。

1. 転がり抵抗力はゼロとする（$F_w = 0$ ）
2. 空力揚力（$FL$ ）もゼロとみなす
3. 路面は平坦であるため、オートバイの前進運動に抵抗する力は空気抵抗力（$FD$ ）のみとなる。

オートバイの圧力中心（空気抵抗力が作用する点）は、その重心と一致します。

さらに抗力に加えて、オートバイには以下の力が作用する。

• 重心に作用する重量 $mg$
• 後輪の接地点で地面がオートバイに加える駆動力 $S$
• タイヤと道路面の間で交換される垂直反作用力 $N_f$ と $N_r$

オートバイの平衡方程式により、重量力$mg$ 、駆動力$S$ 、および抗力$F_D$ が既知である場合に、未知の反作用力$N_f$ と$N_r$ の値を求めることができる。

(⇒) 水平方向の力の平衡

(⇑) 垂直方向の力の平衡

(∩) 重心に関するモーメントの平衡

したがって、タイヤと道路面の間で交換される垂直方向の力は以下の通りである。

前輪の動的荷重

後輪の動的荷重

これらの反作用力は二つの要素で構成される。 最初の項（車輪にかかる静的荷重）は、重量力の分布に依存する。

第二の項（荷重移動）は、駆動力$S$ と重心の高さ$h$ に直接比例し、オートバイのホイールベース$p$ に反比例する。

次に、第二の項に焦点を当てます。「荷重移動」とは、前輪の荷重が減少し、後輪の荷重がそれに対応して増加することを指します。つまり、「荷重が前輪から後輪に移動する」ため、このように呼ばれます。 重心の高さとホイールベースの比率は、h/p が通常 0.3 から 0.45 の範囲である自動車に比べて、オートバイでははるかに高くなります。 車輪にかかる荷重は、重量に対する無次元形式で表すことができます。

前輪にかかる正規化された荷重

後輪にかかる正規化された荷重

ここで、$S_a$ は駆動力$S$ と全重量$mg$ の比率を示します（無次元の駆動力）。

図3-11は荷重移動現象を示しています。正規化された荷重の変化は、以下の特性を持つ二つのオートバイに対する正規化された駆動力の関数として示されています。

• モーターサイクル① $b / p = 0.45 \text {and} h / p = 0.3$
• モーターサイクル② $b / p = 0.45 \text {and} h / p = 0.43$

観察される通り、ホイールベースに対する高い$h / p$ 値を持つオートバイでは、車輪の荷重の変化が大きくなることがわかります。

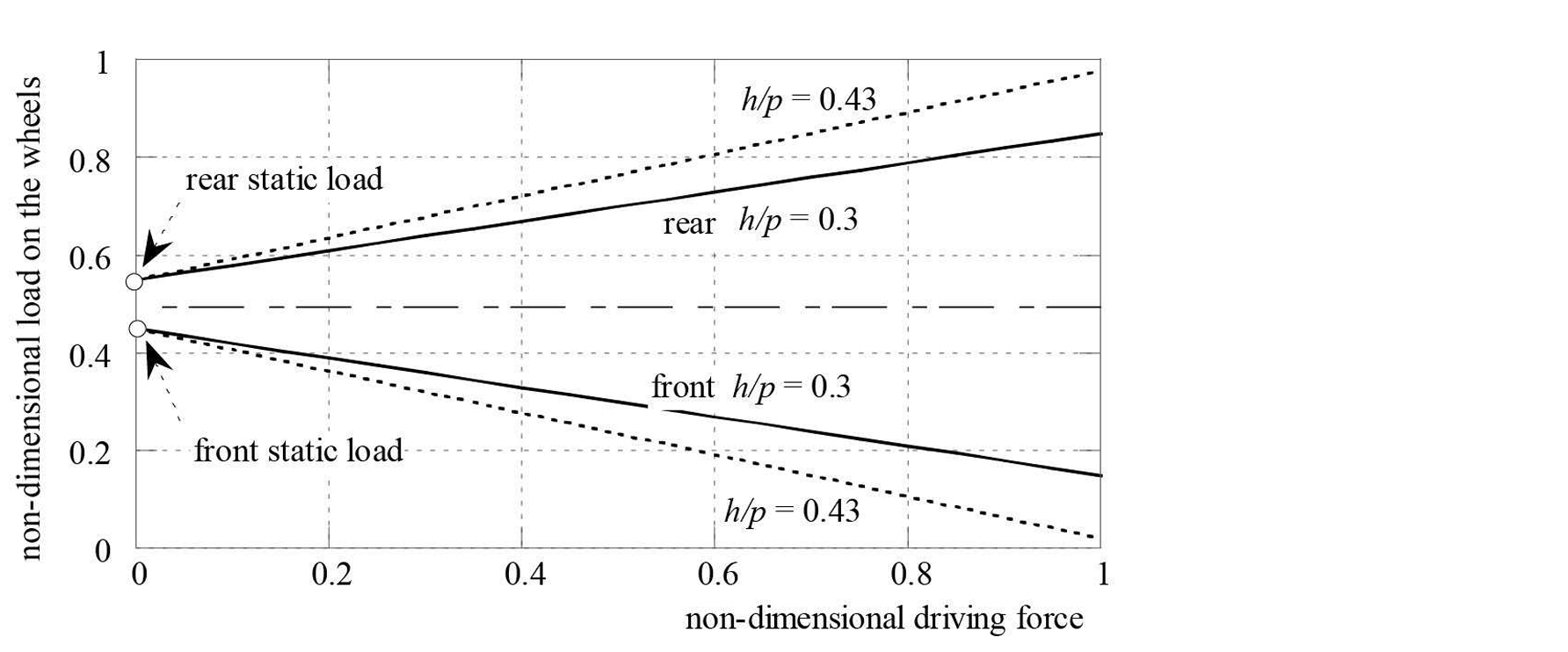
次に、図3-12に示されるオートバイに作用する力を考えてみましょう。重量$mg$ は、車輪に作用する静的荷重の合計と等しい。駆動力$S$ および荷重移動による力$N_{tr}$ 正の符号を持つため上向きに向けられる）が、後輪の接地点に作用します。

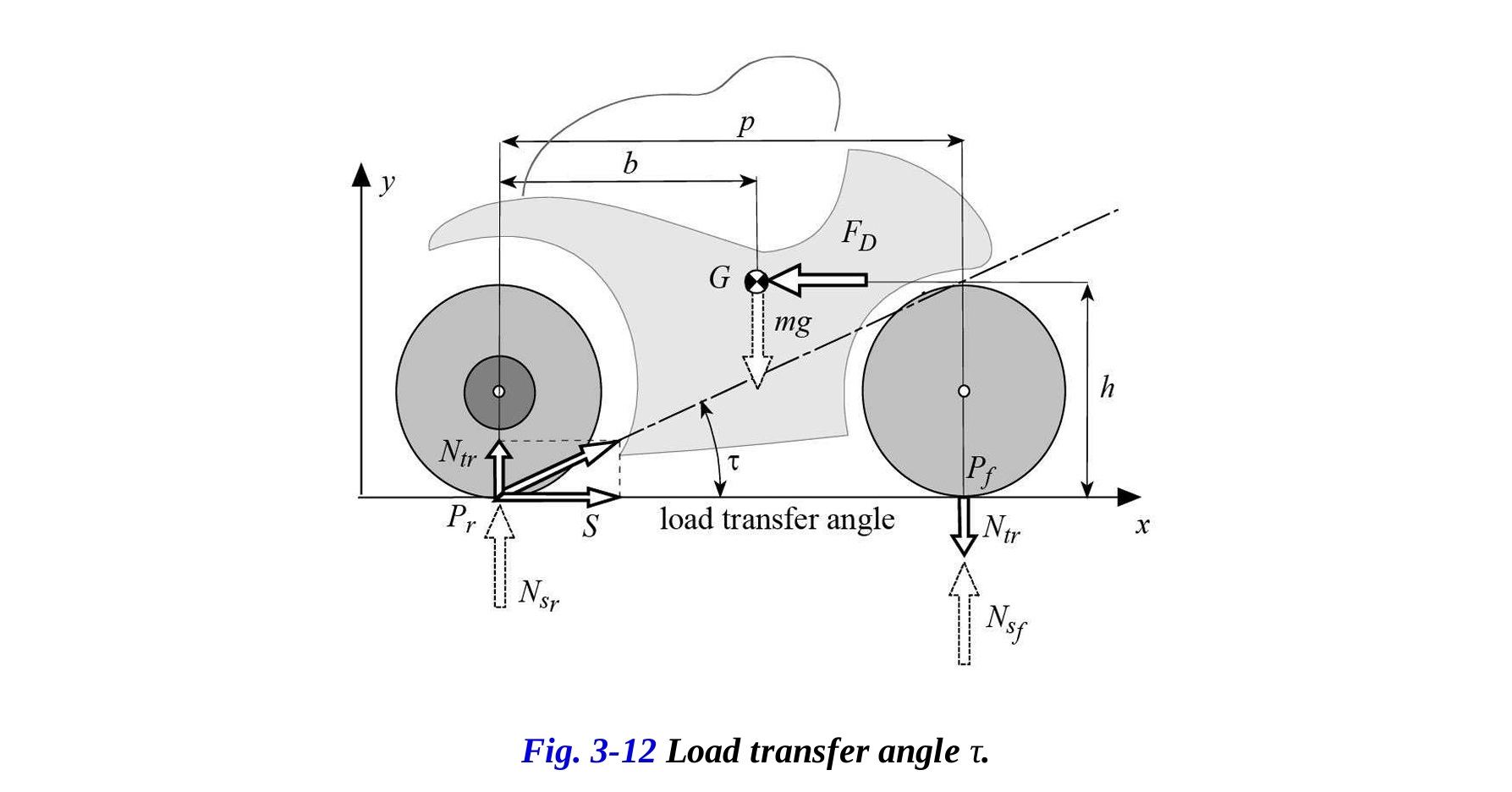
これら二つの力の合力の方向は、道路に対して傾斜しており、その角度は次のようになります。

したがって、これを荷重移動角度と呼びます。

オートバイが平衡を保つためには、この合力は抗力$F_D$ と荷重移動$N_{tr}$ の合力と等しい大きさであり、符号が逆である必要があります。荷重移動は前輪に作用するため（負の符号を持つため下向きに向けられる）、その合力は前輪に作用します。

例４：

質量200kgのバイク（$C_D A = 0.3$ ）は、駆動トラクション係数が1.0である場合、揚力と転がり抵抗を無視した時の最大速度はどれくらいになるか。

バイクの最大仮想前進速度は、前輪が完全に無荷重になり、全荷重が後輪に移動した時に依存する。この条件下では、駆動力係数が1.0で最大駆動力が適用されると、この力は1962 Nに等しく、ドラッグ力と等しくなり、381km/hの速度を生成する。後輪のパワーは208kWある。

例５： 圧力中心が重心と一致していると仮定した場合のウィリー現象によって表されるバイクの限界状態での最大速度を計算せよ。

• 質量 $m = 200 \text {kg}$
• 抗力面積 $C_D A = 0.3 \text {m}^2$
• 揚力面積 $C_L A = 0.1 \text {m}^2$
• 空力的ピッチングモーメント 0
• 重心の前後距離 $b = 0.7 \text {m}$
• 重心の高さ $h = 0.65 \text {m}$
• ホイールベース $p = 1.40 \text {m}$

ウィリー現象の限界に近づく条件では、前輪の垂直荷重がゼロになる。抗力によって生成される荷重移動と揚力の前方成分の合計は前輪の静的荷重と等しい。圧力中心が重心と一致していると考えると、揚力はバイクの前後輪に均等に分布される。そのため、以下のようになる。

この方程式に対応する速度は以下の通りである。

したがって、最大速度は$V = 339 \text {km/h}$ となる。転がり抵抗を無視した場合、後輪でのパワーは少なくとも 147kW でなければならない。この速度では前輪が完全に無荷重となり、バイクのコントロールが不可能になるため、この値は決して達成されるべきでない最大限界として考慮されるべきである。

3.4 過渡的直線運動中のバイク

前の段落で提示された仮定が有効であると仮定して、過渡的直線運動中のバイクを考えてみる。定常状態の運動のために書かれたバイクの平衡方程式は、垂直方向の変位と回転についても依然として有効であると考えられる。

(⇑) 垂直力の平衡

(∩) 重心に関するモーメントの平衡:

ここで、$S$ は加速中の駆動力（+）または減速中の制動力（-）を示す。

バイクが水平運動中の平衡方程式は、加速フェーズにあるかブレーキフェーズにあるかによって特定の特徴を持つようになる。

3.4.1 加速

この場合、駆動力は慣性力と抵抗力の合計に等しい。

(⇒) 水平方向の力の平衡 $S^* = F_D + m^* \ddot{x}$

ここで、$S^* = T (\omega_m / V)$ はエンジントルク$T$ にエンジン回転数と前進速度の比率$\omega_m / V$ を掛けて得られる駆動力であり、$m^*$ は回転慣性の要素も考慮したバイクの質量を示す。この質量は、バイクの総運動エネルギー（回転部分の回転運動エネルギーと平行移動の運動エネルギーの合計）を、1つの質量$m^*$ （等価質量）によって構成される等価システムの運動エネルギーに等しくすることで計算される。動力学の観点から見ると、等価質量の運動法則は実際のバイクの運動法則と等しい（図3-13参照）。

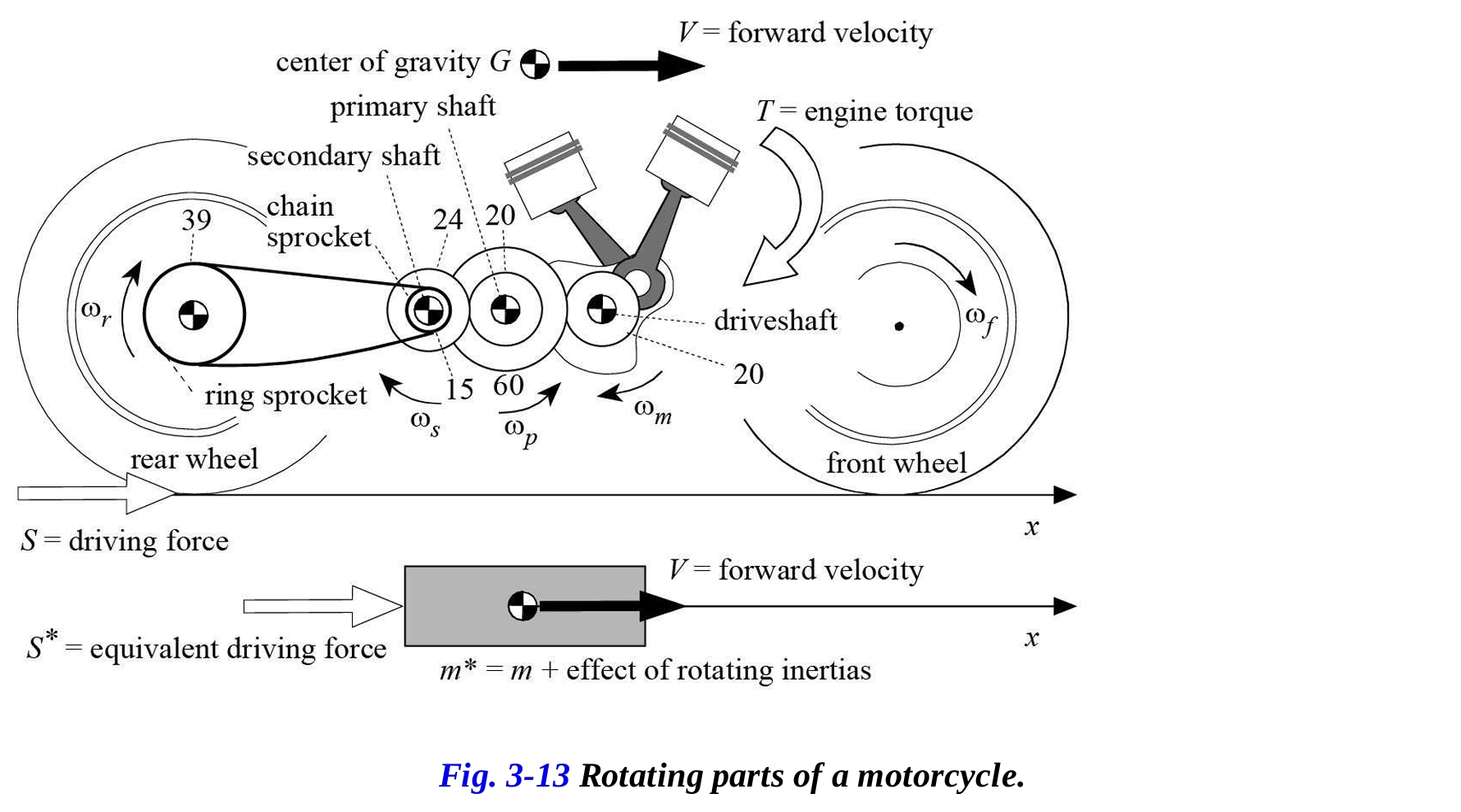
運動エネルギーを等式化すると、次の式が得られる。

ここで:

• $m$ バイクの質量
• $I_{W_r}$ 後輪の慣性
• $I_{W_f}$ 前輪の慣性
• $I_{W_p}$ 一次シャフト（クラッチを含む）の慣性
• $I_{W_s}$ 二次シャフトの慣性
• $\tau$ 速度比
• $I_{W_m}$ エンジンの慣性（クランクシャフト、逆回転シャフトを含む）、クランクシャフトに還元されたもの（この慣性は、往復運動をする質量の変動項を無視する初期近似において一定と見なすことができる）

後輪の角速度とバイクの前進速度の比率は以下の通りです。

前輪の角速度とオートバイの前進速度の比率は以下の通りです。

二次軸の角速度とオートバイの前進速度の比率は以下の通りです。

ここで、$\tau_{s,r}$ はピニオンとリアスプロケットの間の変速比です。

一次ギア軸の速度とオートバイの速度の比率は以下の通りです。

ここで、$\tau_{p,s}$ は一次ギア軸と二次ギア軸の間の変速比を示します。駆動スプロケットは二次軸に固定されています。

エンジン軸の速度とオートバイの前進速度の比率は以下の通りです。

ここで、$\tau_{m,p}$ はエンジンクランク軸と一次軸の間の変速比を示します。

定常状態の運動の場合、ホイールにかかる動的荷重は次の方程式で示されます。

前輪にかかる動的荷重:

後輪にかかる動的荷重:

例6

以下の特性を持つレーシングバイクを考え、等価質量を求めましょう。

• 総質量（バイク + ライダー） $m = 205 \text {kg}$
• 前輪半径 $R_f = 0.30 \text {m}$
• 後輪半径 $R_r = 0.32 \text {m}$
• 前輪の慣性モーメント $I_{W_f} = 0.6 \text {kgm}^2$
• 後輪の慣性モーメント $I_{W_R} = 0.8 \text {kgm}^2$
• エンジンの慣性モーメント $I_{W_m} = 0.05 \text {kgm}^2$
• 一次軸の慣性モーメント $I_{W_p} = 0.005 \text {kgm}^2$
• 二次軸の慣性モーメント $I_{W_s} = 0.007 \text {kgm}^2$
• 駆動輪スプロケットの変速比 $\tau_{s,r} = 2.6$
• 一次・二次ギア軸の変速比 $\tau_{p,s} = 0.9 \text {(in IV gear)}$
• エンジンと一次軸の変速比 $\tau_{m,p} = 2$

速度比は次のようになります:

• $\tau_r = 3.125$
• $\tau_f = 3.33$
• $\tau_m = 2 \cdot 0.9 \cdot 2.6 \cdot \dfrac {1} {0.32} = 14.63$
• $\tau_p = 0.9 \cdot 2.6 \cdot \dfrac {1} {0.32} = 7.313$
• $\tau_s = 2.6 \cdot \dfrac {1} {0.32} = 8.125$

速度比が分かれば、等価質量$m^*$ を以下のように計算することができます。

$m^* = m + I_{W_r} \cdot \tau_r^2 + I_{W_f} \cdot \tau_f^2 + I_{W_m} \cdot \tau_m^2 + I_{W_p} \cdot \tau_p^2 + I_{W_s} \cdot \tau_s^2$

$205 + 7.81 + 6.67 + 10.69 + 0.27 + 0.46 = 230.9 \text {kg}$

重要なことは、エンジンが速度比が高いために非常に重要な役割を果たすことです。このため、慣性モーメントの値が低くても関係があります。

等価質量は明らかに、ギアがどれに噛み合っているかに依存します。ギアシフトの変速比は、最初のギアでは約3程度（減速ギアとして機能します）から始まり、最も高いギアではほぼ1に近い値（約0.7程度まで低下することもあります）になります。最小の慣性を持つ最大値は、最初のギアに噛み合った時に達成されます。

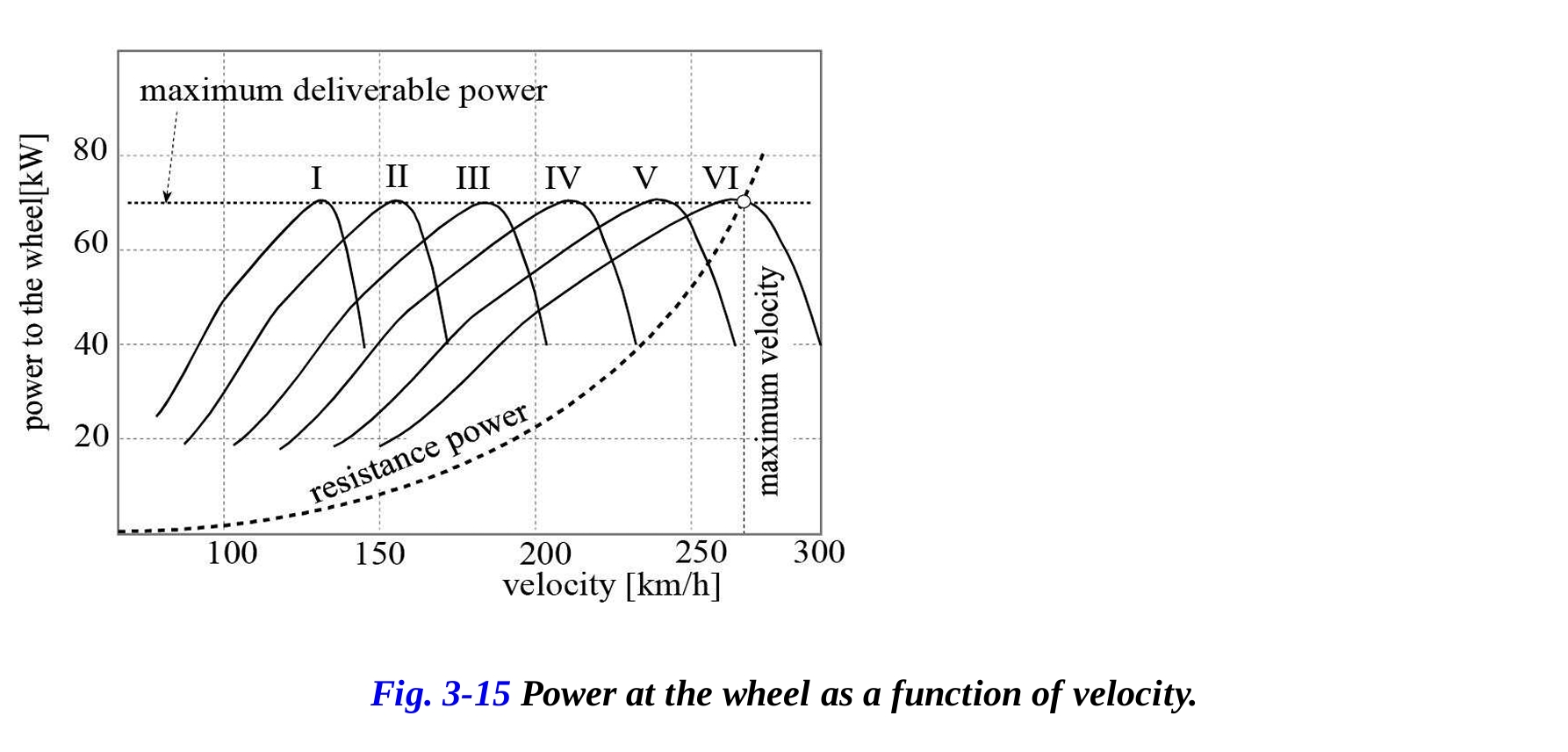
図3-14は、レーシングバイクの各ギアにおける速度に対する車輪への駆動力の変化を示しています。描かれた曲線は、抵抗力（空気抵抗と転がり抵抗力の合計）の変化も示しています。

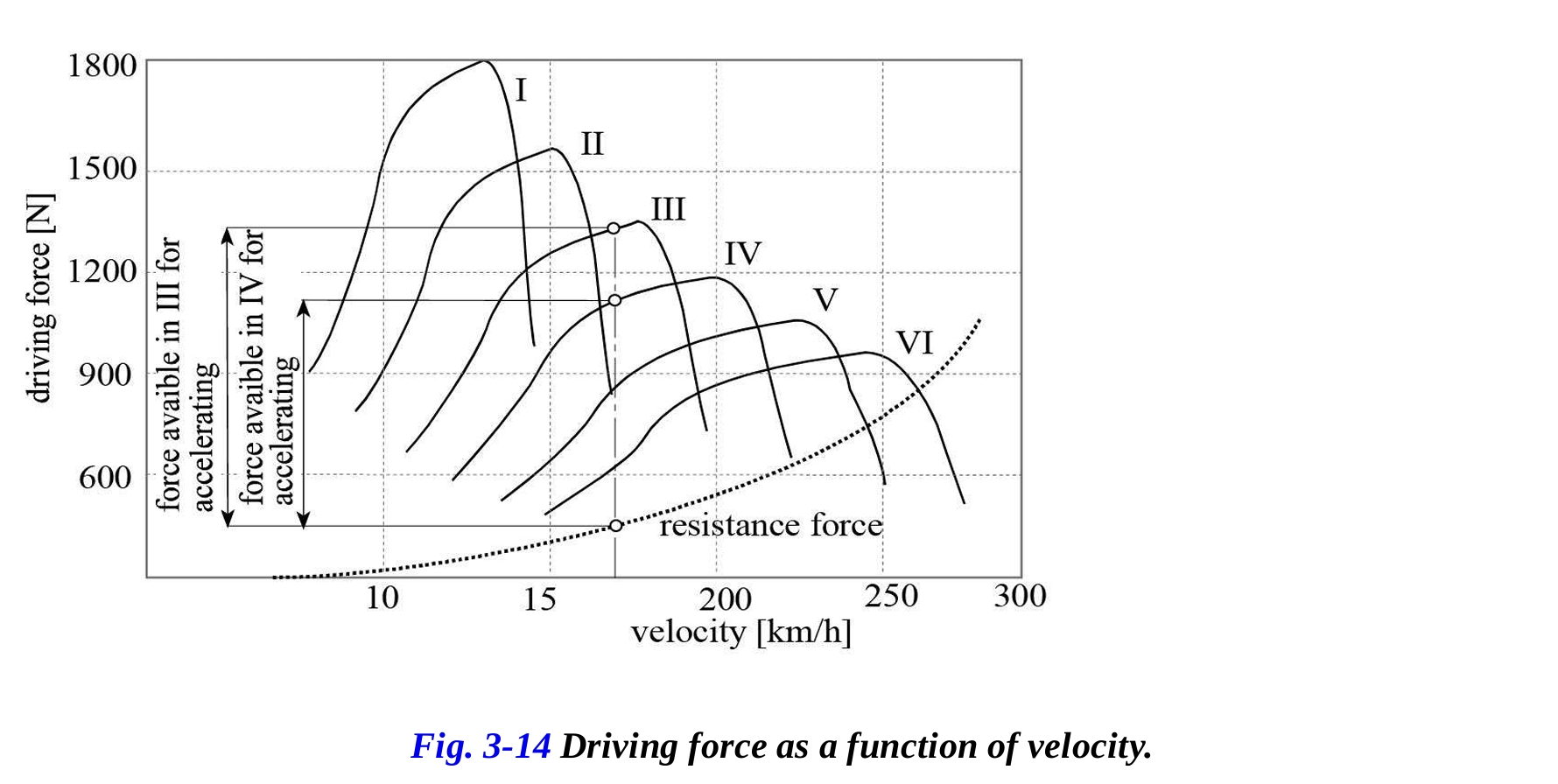
さて、レーシングバイクが図に示された特定の速度で３速ギアで進むと仮定しましょう。その時の駆動力は、そのギアで利用可能な最大駆動力よりも低く、抵抗力よりも大きいため、残りの駆動力を加速や坂道を同じ速度で登るために使用することができます。同じ速度でより高い変速比を考慮すると、加速に使用できる駆動力が少なくなることがわかります。速度が徐々に増加すると、より高い変速比への移行により、利用可能な割り当てが低くなります。最大速度は、最高ギアで抵抗力が駆動力と同じになると明らかにされます。

駆動力曲線と抵抗力曲線は、パワーの観点からも比較することができます。各変速比ごとに有効な車輪へのパワーの図を得るために、それぞれの曲線を対応する前進速度で乗算します。図3-15は、車輪への有用なパワー曲線と抵抗パワー曲線を前進速度の観点で示しています。この場合も、抵抗パワー曲線が最高ギアで有用なパワー曲線と交差する点が、到達可能な最大速度を決定します。

さて、エンジンパワーが速度の増加に伴って一定であると仮定しましょう。これは、効率が速度に依存しない理想的なケースであり、図3-15に水平線で表されています。最大のバイク加速度は、次の微分方程式を積分することによって決定できます。

ここで、$P_{\text{max}}$ はエンジンの最大出力を示します。前述の微分方程式の数値積分を実行することで、バイクが達成可能な最大加速度を計算することができます。これは明らかに理想的な値であり、実際にはバイクの最大加速度は後輪タイヤのグリップ、バイクのウイーリング、有限のギア数などによって制限される可能性があります。

例7

以下の特性を持つバイクを考えてみましょう。質量が変化することが速度と加速度にどのように影響するかを調べてみましょう。

• 等価質量 $m^* = 230.9 \text {kg}$
• 正面投影面積 $A = 0.6 \text {m}^2$
• 空気抵抗係数 $C_D = 0.7$

エンジンの最大出力は$P_{\text{max}} = 70 \text{kW}$ であり、道路への最大伝達可能な駆動力は 4000N です。

運動の微分方程式を数値積分して得られる速度対時間の曲線は図3-16に示されています。質量が30%軽いバイクはより大きな加速度を示しますが、最大速度は変わりません。

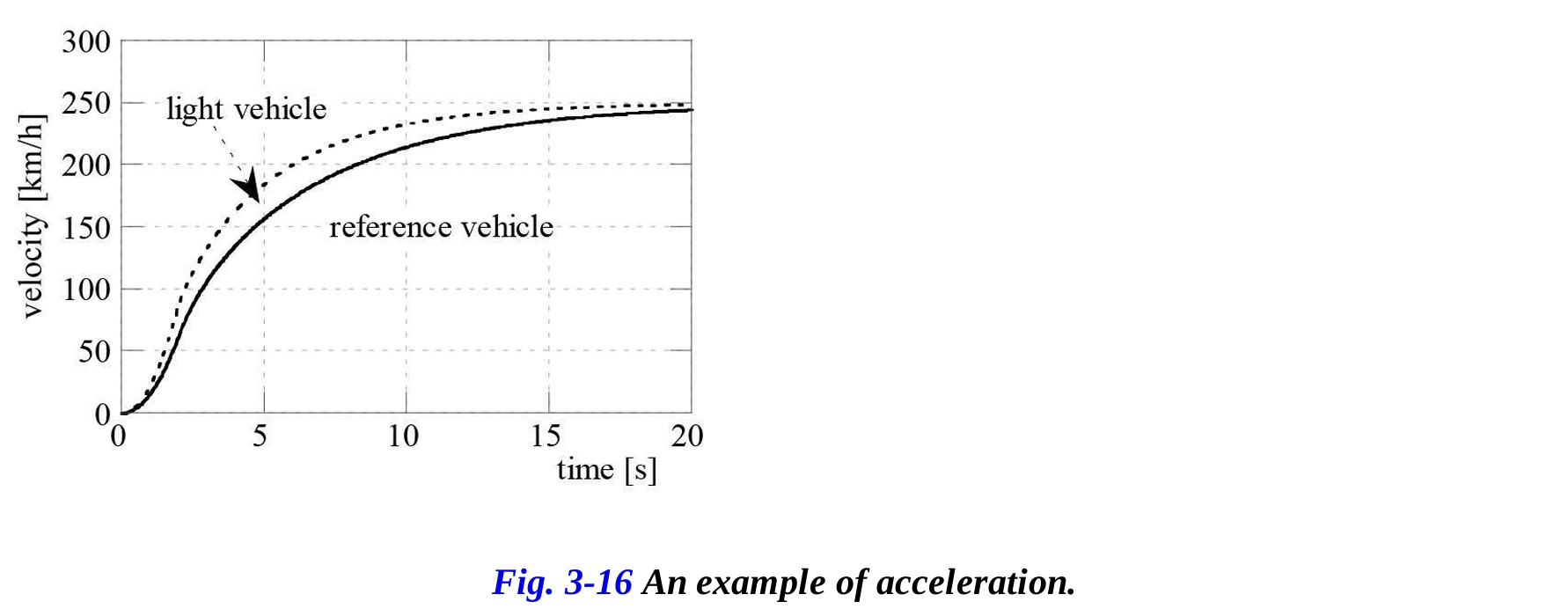
実際の場合、加速度（曲線の勾配）は実際には低くなることがあります。これは、ギアを変えるために必要な時間間隔があり、その間、有効な駆動力がゼロになるからです。さらに、初期段階では、先に述べたように、後輪の滑りや可能なウイーリングのために常に全ての駆動力を適用することができるわけではありません。

3.4.2 牽引制限された加速度

図3-17に示すように加速するバイクを考慮し、転がり抵抗力$F_w$ を無視できると仮定した場合、運動方程式は次のように書けます。

ここで、$S$ は車輪にかかる駆動力を示し、$F_D$ は抗力を示します。エンジンが十分なパワーを持っていると仮定すると、駆動力は、駆動トラクション係数$\mu_p$ と鉛直荷重$N_r$ の積で与えられる最大力に等しいか、それ以下でなければなりません。

以下の式を用いれば、

次を得ることができます。

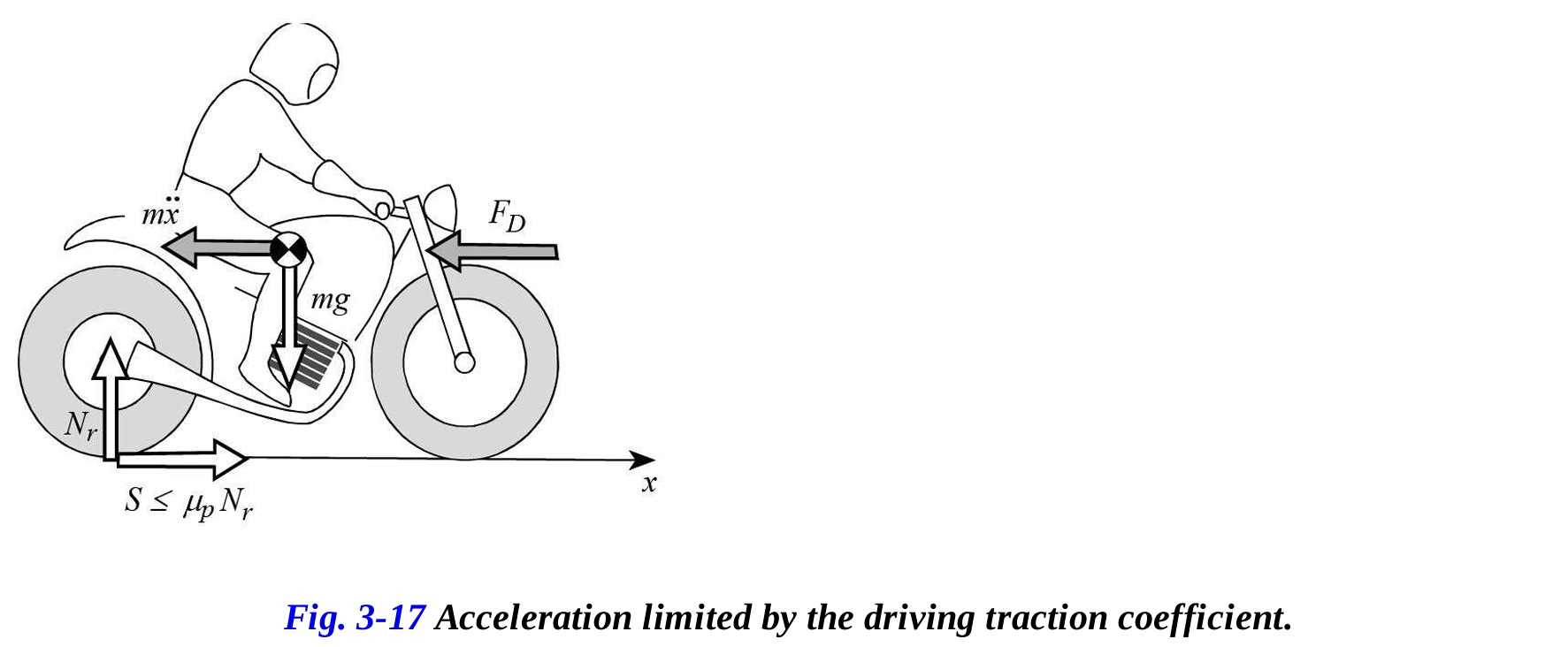
最大加速度は、抵抗力$F_D$ がゼロであるとき、つまり低速から始まります。速度が増加するにつれて、摩擦制限条件下での加速度は減少します。これは、駆動力の一部が抵抗力と等しくなり、そのため加速に使用できなくなるからです。

3.4.3 ウイーリング制限された加速度

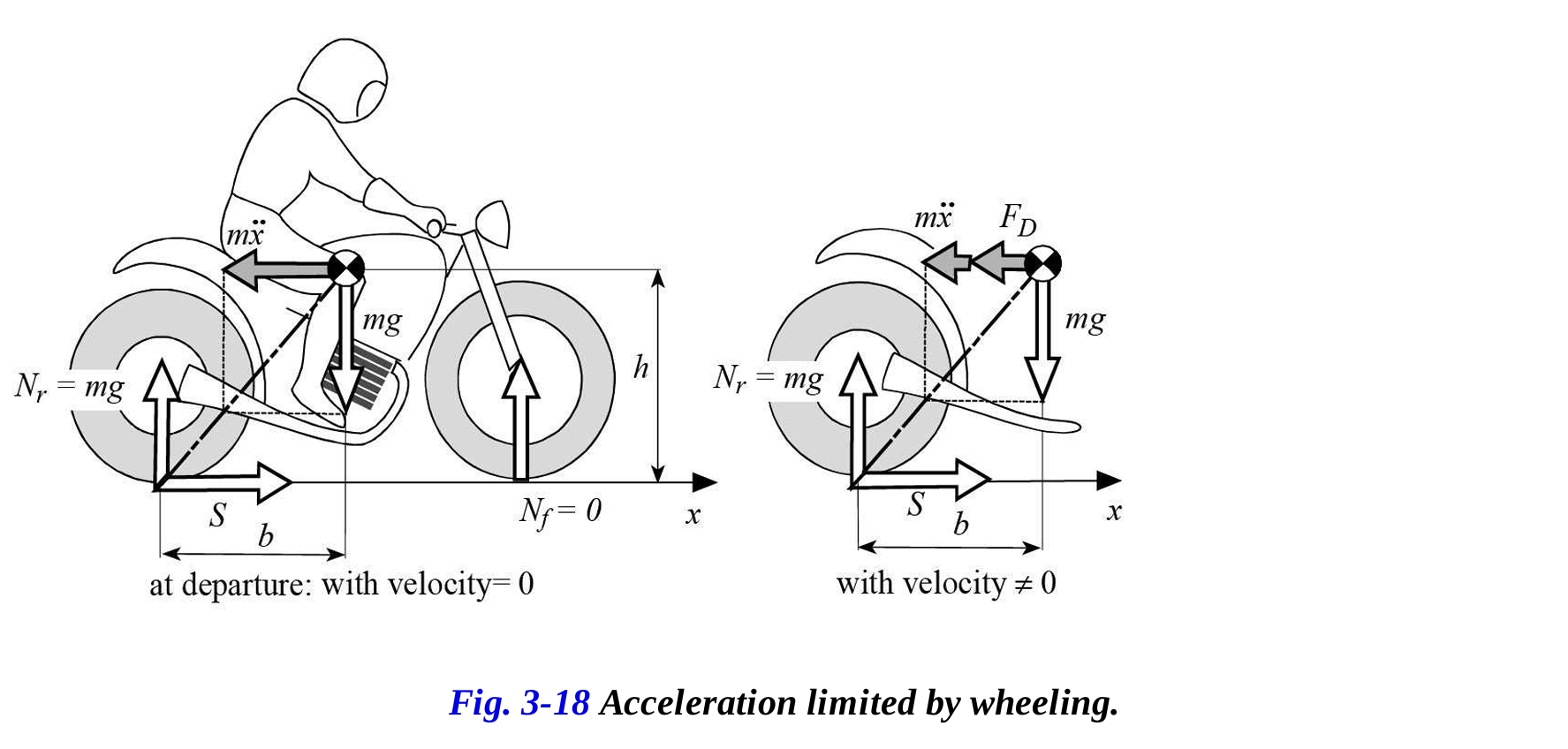
ウイーリングが始まる瞬間の制限条件は、前輪への荷重がゼロに減少するときに達成されます（図3-18参照）。この状況は以下の関係式で表されます。

これから以下を得ます。

ウイーリングが起こりそうな加速度は、その時点での比率$b/h$ に依存します。前進速度が徐々に増加すると、ウイーリング現象が始まる加速度は低下します。これは、ウイーリングの運動が抗力$F_D$ によっても促進されるためです。抗力の値は速度とともに増加します。

例8

以下の特性を持つバイクを考慮します。初速0 km/hと100 km/hにおけるウイーリング制限された加速度を求めます。

• 総質量 $m = 200 \text{kg}$
• 正面投影面積 $A = 0.7 \text{m}^2$
• 空気抵抗係数 $C_D = 0.6$
• 揚力係数 $C_L = 0$
• 重心の縦方向距離 $b = 0.58 \text{m}$
• 重心の高さ $h = 0.62 \text{m}$
• ホイールベース $p = 1.35 \text{m}$

バイクの最大加速度は、後輪の摩擦限界であるときの駆動力係数によって、速度がゼロおよび100 km/hの場合のグラフで示されます（図3-19）。速度が増加するにつれて、最大加速度は減少します。これは、駆動力の一部が抗力力と等しくなり、加速に使用できないためです。

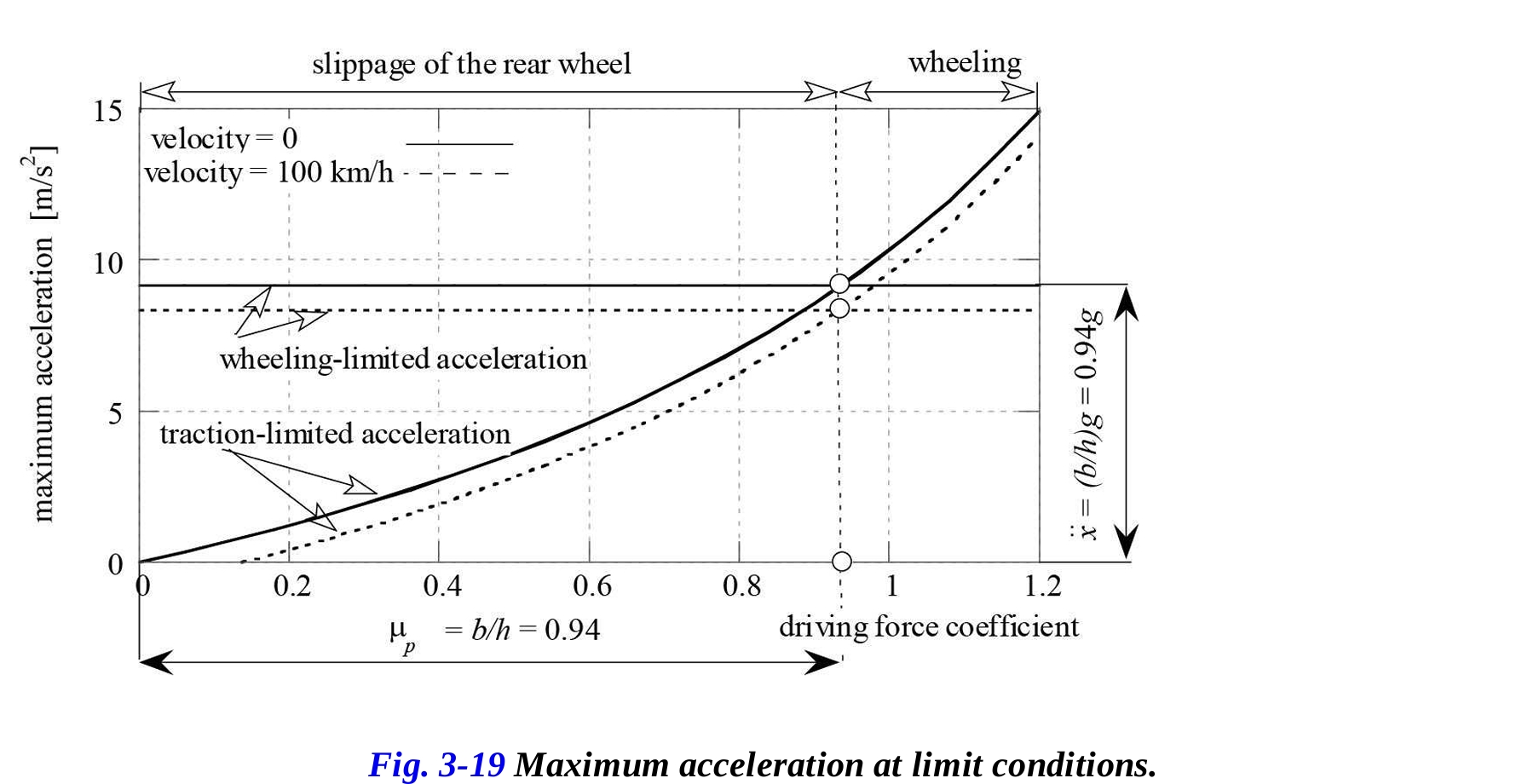
バイクのウイーリング制限された加速度は、0 km/hと100 km/hにおいてもグラフに示されています。ウイーリング制限された加速度を表す水平線は、加速度が駆動力係数に依存しないことを示しています。

ウイーリング制限された加速度は、駆動トラクション係数が以下の値であるとき、牽引制限された加速度に等しくなります。

また、加速度は、

係数が比率$b/h$ よりも低い場合、バイクは加速中に前輪を持ち上げることはありません。なぜなら、後輪の滑りがウイーリング加速度に達するのを防いでいるからです。同様に、係数が比率 b/h よりも高い場合、バイクは駆動トラクション係数で最大加速度に達する前に前輪が持ち上がるため、その制限値に達することができません。これらの考慮事項から、バイクのウイーリングや後輪の滑りを避けるために、エンジンが提供できる最大トルクを制限することが適切であるとされています。

今考慮しているケースでは、図3-19に示されているように、加速度は$9.18 \text{m/s}^2$ に等しいです。この値は、バイクに 1835 N の駆動力を適用することで得られます。バイクのエンジンがそのような大きさの有用な力を車輪に供給できない場合、自然にウイーリングは発生しないでしょう（ただし、ライダーが移動やピッチング動作を利用して前輪を持ち上げることは可能です）。

3.4.4 ブレーキング

運転の安全性には、効率的なブレーキシステムに加えて、ライダーがさまざまな条件下で必要な停止距離を判断し、ブレーキシステムの全ての可能性を活用して、特に後輪ブレーキを利用して最適な方法でブレーキをかけることが求められます。実際、多くのバイクライダーは後輪ブレーキを忘れがちですが、特定の状況では有用な貢献をします。カーブに入る際のブレーキングや、予期せぬ障害物がバイクの前に現れたとき（特に路面のグリップが不安定な場合）の直線運動中のブレーキングにおいて、その正しい使用が重要です。

後輪ブレーキの急停止時の役割

カーブに入る際の後輪ブレーキの使用は非常に有用です。熟練したライダーは、バイクを減速させるだけでなく、ヨーモーション（横方向の回転運動）を制御するためにも後輪ブレーキを使用します。カーブに入る際に後輪ブレーキをかけることで、サイドスリップ角が増加し、それによりバイクのヨーモーションが増加します。

急減速時には、特に荷重移動により後輪の荷重がゼロに近づくと、危険な状態が発生する可能性があります。バイクが完全に直進していない場合、前輪ブレーキの力と減速の慣性力がモーメントを生成し、それがバイクをヨーにする傾向があります。これが図3-20に示されています。

図3-20に示されているように、前輪ブレーキ力と慣性力によって生成されるトルクは、車両をヨーさせる傾向があります。これに対して、後輪ブレーキ力の存在は、車両を整列させ安定させるトルクを生成し、これは図3-21で直感的に理解できます。

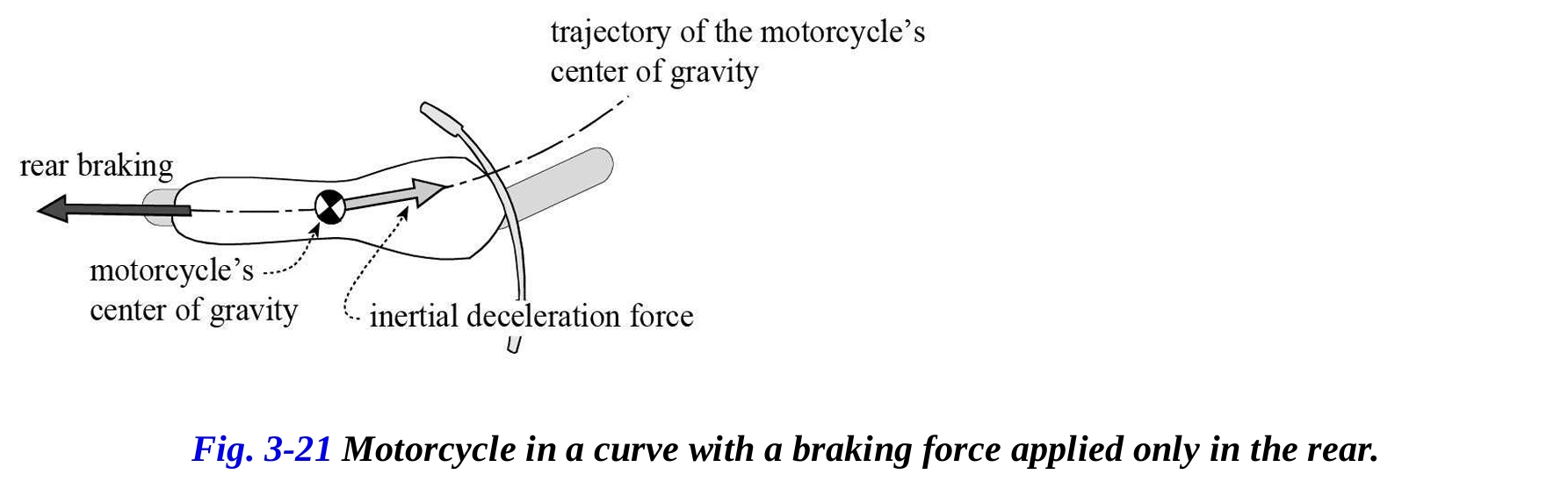
これらの簡単な考慮事項から、前輪ブレーキと後輪ブレーキの適切な利用が車両の安定性に対して良い効果をもたらすことが示唆されます。

ブレーキング時の荷重移動

後輪ブレーキの役割を滑り限界で評価するためには、バイクに作用する力に関するいくつかのポイントを考慮する必要があります。減速中は前輪の荷重が増加し、後輪の荷重が減少するため、荷重が後輪から前輪に移動します。ブレーキをかけているバイク（図3-22参照）を考慮し、ニュートンの法則をバイクに適用すると、後輪から前輪への荷重移動を計算することができます。

（⇒） 水平方向の力の平衡 $m\ddot{x} = -F_f - F_r$

（⇑） 垂直方向の力の平衡 $mg - N_r - N_f = 0$

（∩） 重心周りのモーメントの平衡 $-Fh - N_rb + N_f(p - b) = 0$

ここで、$F$ （全体のブレーキ力）は前輪のブレーキ力$F_f$ と後輪のブレーキ力$F_r$ の合計を示します。前輪の動的荷重は静的荷重と荷重移動の合計に等しくなります。

一方、後輪の動的荷重は、静的荷重と荷重移動の差に等しくなります。

荷重移動$F h/p$ は、全体のブレーキ力および重心の高さに比例し、ホイールベースに反比例することがわかります。ブレーキング中にタイヤの滑りを防ぐためには、そのタイヤに作用するブレーキ力の値が、そのタイヤに作用する動的荷重と局所的なブレーキトラクション係数の積を超えてはなりません。この積は、タイヤに適用可能な最大ブレーキ力、つまり滑りの限界でのブレーキ力を表します。

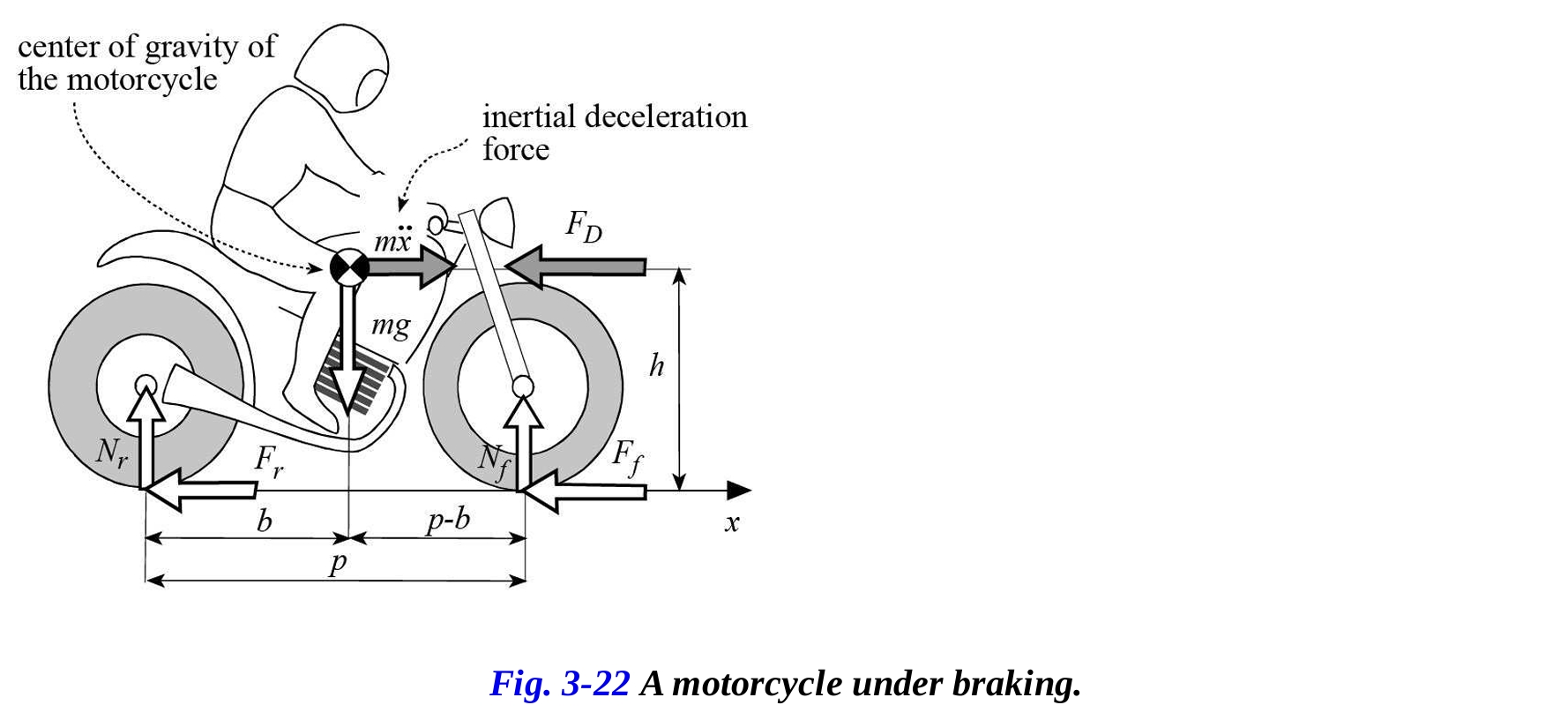
$\mu_{p_f}$ と$\mu_{p_r}$ を、それぞれ前輪と後輪に対するブレーキトラクション係数とすると、スリップの限界における全体のブレーキ力は、以下の式で表されます。

通常、ブレーキング中にはスリップの限界に達することはありません。したがって、ブレーキ力は前輪と後輪のブレーキ力係数（μとして示され、それぞれの縦力と対応する垂直荷重の比として定義される）に依存します。

図3-23は、ブレーキング力に関する動的荷重の変化を示しています。車輪への荷重とブレーキング力は、重量に対して無次元化されています。このバイクは、その前後輪に対して50%ずつの静的荷重分布を持ち、つまり重心はホイールベースの中心線上に位置しています。

仮に使用されているブレーキング力係数が非常に低い場合、例えば両輪ともにμ = 0.2とすると、グラフから分かるように、車輪への動的荷重は後輪が約0.4、前輪が約0.6となります。これらの条件下では、もしリアブレーキが使用されない場合、最大可能なブレーキング力の40%が使用されません。しかし、ブレーキング力係数が非常に高い場合、例えばμ = 0.9とすると、図3-23に示されるように、前輪への荷重は0.95であり、後輪への荷重はほとんど無視できる0.05です。この場合、リアブレーキ力の可能な貢献はほとんど無視できるほどです。

まとめると、次の一般的な原則が述べられます。

• ブレーキトラクション係数に応じて、最適なブレーキ力の分布は異なります。
• オプティマルな道路や高グリップのタイヤ（摩擦係数が高い場合）では、リアブレーキはほとんど役に立ちませんが、滑りやすい路面（摩擦係数が低い場合）では不可欠となります。

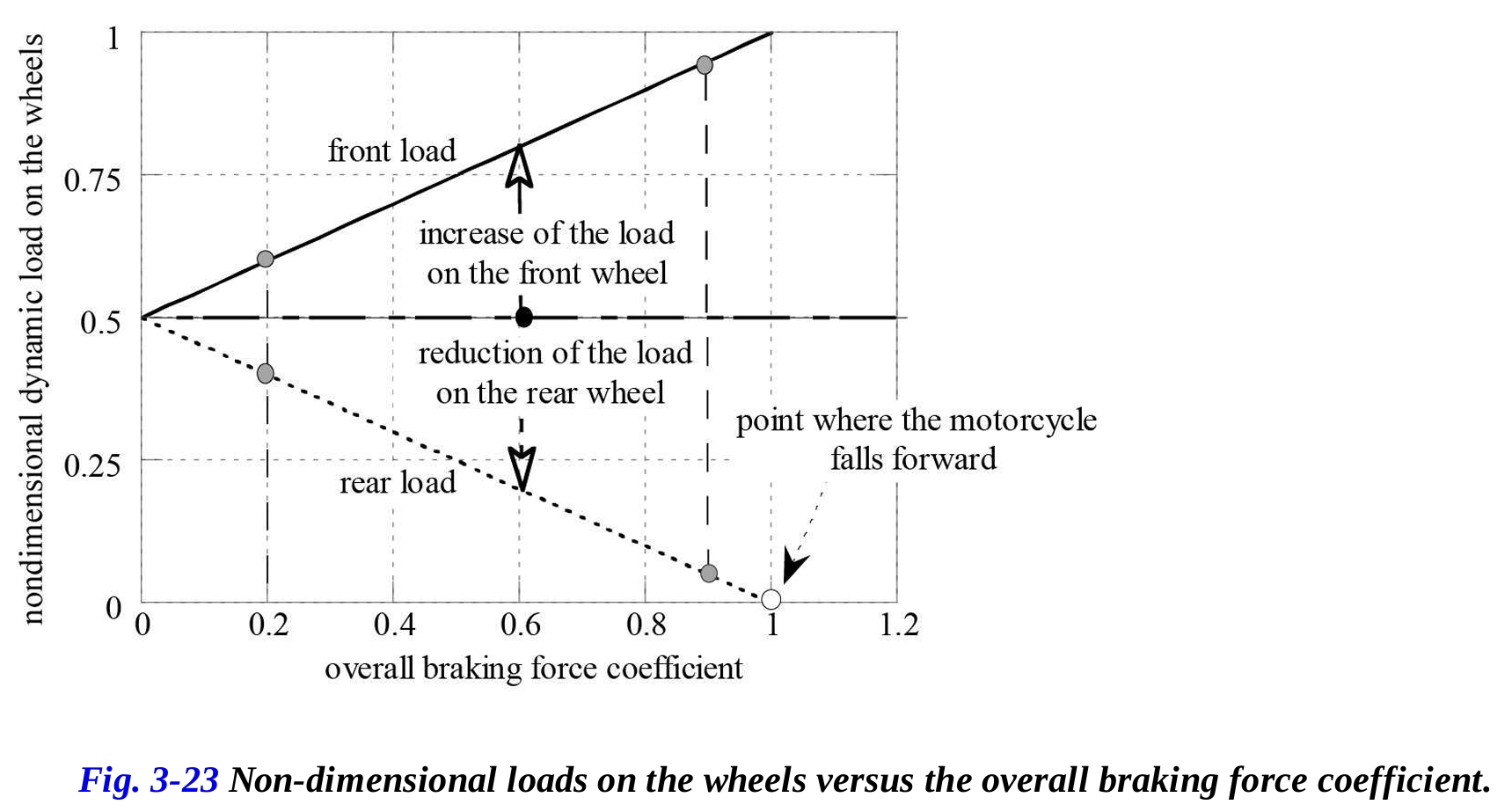
3.4.5　オートバイの前方転倒

図3.23は、全体のブレーキ力が増加すると、後輪への荷重がゼロになることを示しています。この限界状態は、動的荷重が後輪でゼロになるときにオートバイが前方に転倒することを表しています。

この状況では、前輪への動的荷重はオートバイの重量に等しくなり、動的荷重とブレーキ力の合力の方向はオートバイの重心を通過します。重心に関するモーメントの平衡の方程式は、転倒時のブレーキ力を表す式を提供します。

この限界ブレーキ力の値が低いことは、前方転倒の傾向が増すことを示しています。したがって、オートバイが軽量で重心が高く、前方に位置している場合、前方転倒が起こりやすくなると結論付けることができます。

転倒が差し迫っている状況下での運動方程式は、空気抵抗を無視すると次のようになります。

最大減速はgで表され、重心から前輪の接地点までの縦距離に比例し、重心の高さに反比例します。

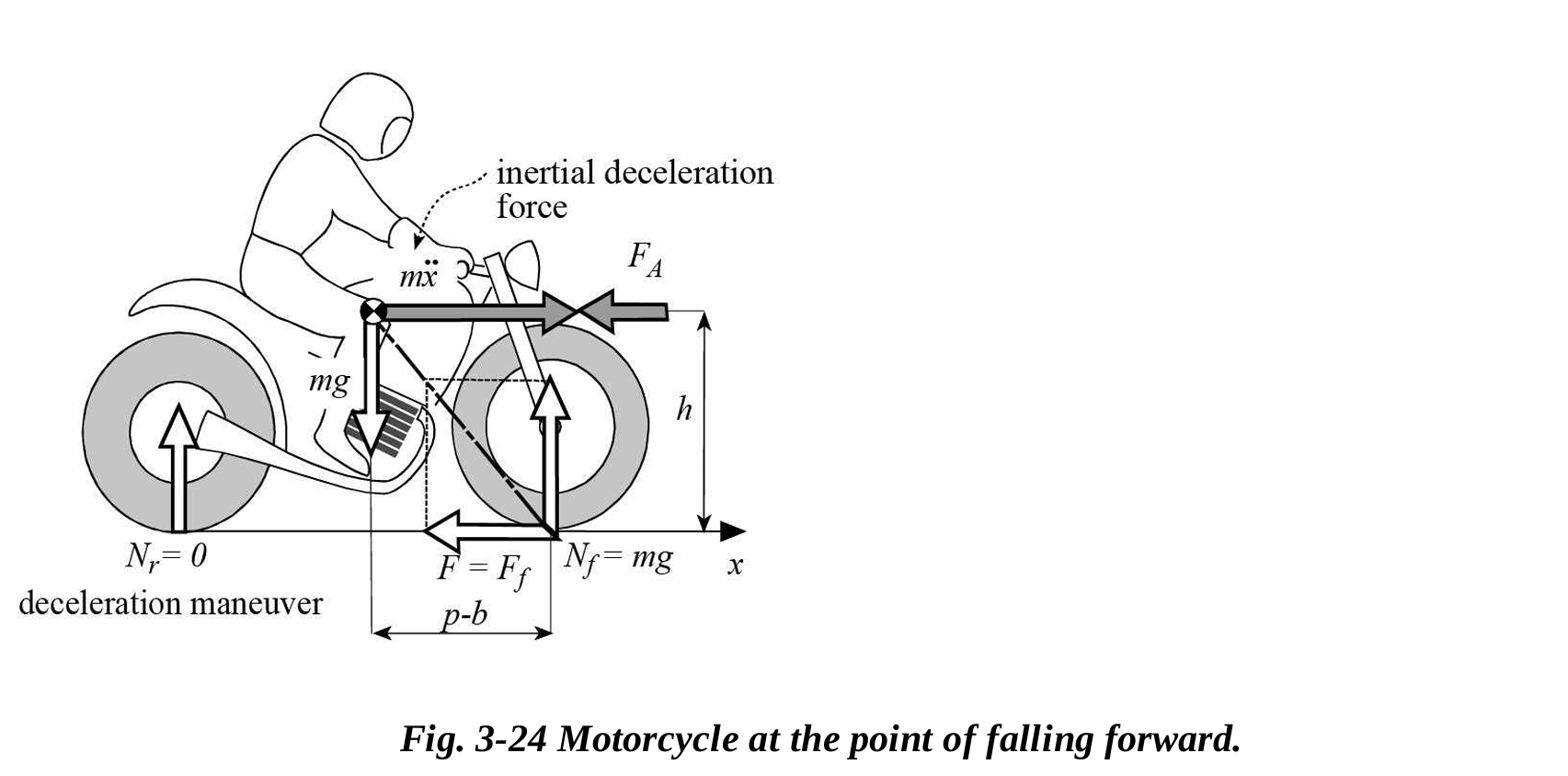
転倒限界における減速は、オートバイの重さではなく、重心の位置のみに依存することに注意することが重要です。この限界値を高めるためには、オートバイの重心を低くし、できるだけ後方に配置する必要があります。空気抵抗力を考慮に入れると、

最大減速は、質量と速度の両方に依存します。

例9

前後輪に50%ずつ荷重が分配されている場合、ホイールベースが1400mmで、重心の高さが700mmであるときの前方転倒限界での最大減速はどれくらいでしょう。 最大減速が重力に等しいことは簡単に確認できます。速度も考慮に入れると、空気抵抗力の影響により、速度が増加するにつれて減速も増加します。速度が100km/h、抗力面積が0.4m²、質量が200kgの場合、最大減速は1.26gに等しくなります。一方、速度が200km/hの場合、最大減速は1.54gに増加します。明らかに、リアホイールの荷重がゼロの状態で転倒限界までブレーキをかけるのは非常に難しく、不可能ではないにしても難しいです。この限界に近づく状況では、最も優れたライダーは1.1gから1.2gの減速を達成することができます。

3.4.6　最適なブレーキング

水平力の平衡方程式$m\ddot{x} = -F_f - F_r$ および垂直力の平衡方程式$mg - N_r - N_f = 0$ により、前後のブレーキ力係数を用いてブレーキ減速を次のように表すことができます。

摩擦の限界条件において、両輪のブレーキトラクション係数が等しい場合（$\mu = \mu_{p_f} = \mu_{p_r}$ ）、最大可能な減速の値は次のようになります。

両輪で限界条件に達するためのブレーキ力の関係は、（等しいブレーキトラクション係数）同時に次のようになります。

この関係は、ブレーキ力係数μの値を考慮して、最適なブレーキングを実現するためにどのようにブレーキ力を分配すればよいかを示しています。

図3-25には、各輪に使用されるブレーキ力係数の観点からブレーキと減速の分布曲線が示されています（重力加速度$g = 9.81 \text{m/s}^2$ と仮定）。図3-25では、特に前輪に関してブレーキ力係数が増加すると減速が増加することがわかります。この振る舞いは理解できます。なぜなら、すでに説明したように、ブレーキング中には後輪から前輪への荷重移動が発生するからです。実線は前輪と後輪の間でのブレーキ分布を表しています。

横軸はリアホイールのみでのブレーキング（0/100）、縦軸はフロントホイールのみでのブレーキング（100/0）を示しています。図は、特にブレーキトラクション係数が低い場合にリアブレーキの有用性を示しています。その有用性は、非常に高いブレーキトラクション係数が存在する場合にほぼ無視できるほどに減少します。

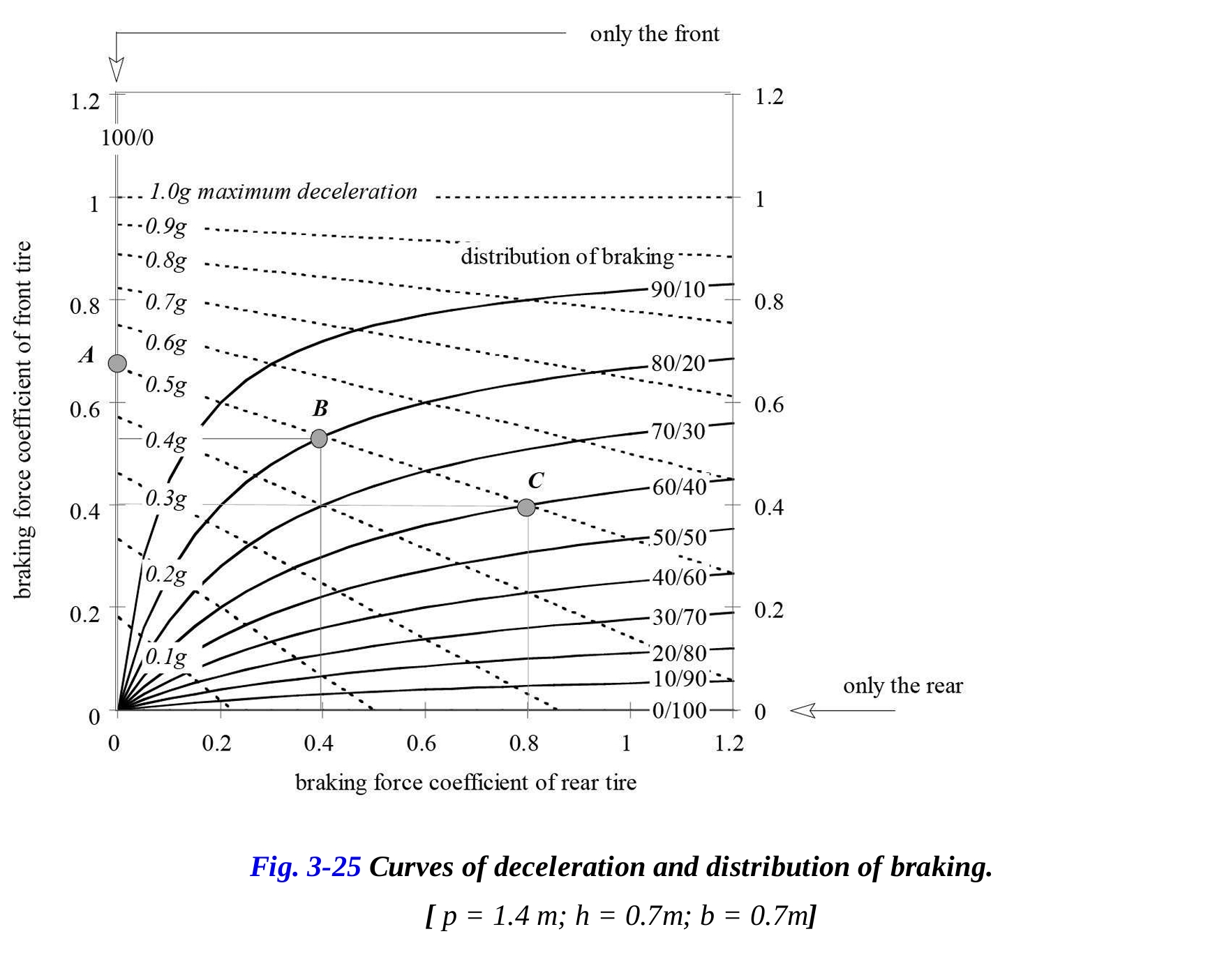
このデータを考慮すると、前方転倒の限界条件が発生するのは、減速が約1.0gに近い場合です。この場合、1.0gの曲線が最大可能な減速となります。

例えば、減速を0.5gにしたい場合、前輪と後輪のブレーキの使用の組み合わせは無数に存在します。例えば、前輪のみでブレーキをかけると、前輪のブレーキ力係数が0.68であれば0.5gの減速が得られます（点A）。一方で、前輪80%、後輪20%のブレーキ力分布では、前輪のブレーキ力係数が0.55、後輪が0.4であれば0.5gの減速が得られます（点B）。別の可能性として、点Cでは前輪60%、後輪40%のブレーキ力分布で、後輪の使用が増え、前輪の使用が減少します。

次に、前後タイヤのブレーキトラクション係数が同じであると仮定します。図3-26は、2つのタイヤに同じブレーキ係数を使用することで、最大可能な減速が得られることを示しています。例えば、前後輪ともにブレーキ力係数が0.8の場合、前輪90%、後輪10%のブレーキ分布で最大減速（0.8g）が得られます。この分布で両輪の最大利用が可能となります。図はさらに、前輪のみを使用すると0.67gの減速、後輪のみを使用すると0.29gの減速が得られることを示しています。道路がより滑りやすく、両輪のブレーキトラクション係数が0.4の場合、異なる分布（70/30）で最適なブレーキが行われ、0.4gの減速が得られることが示されています。

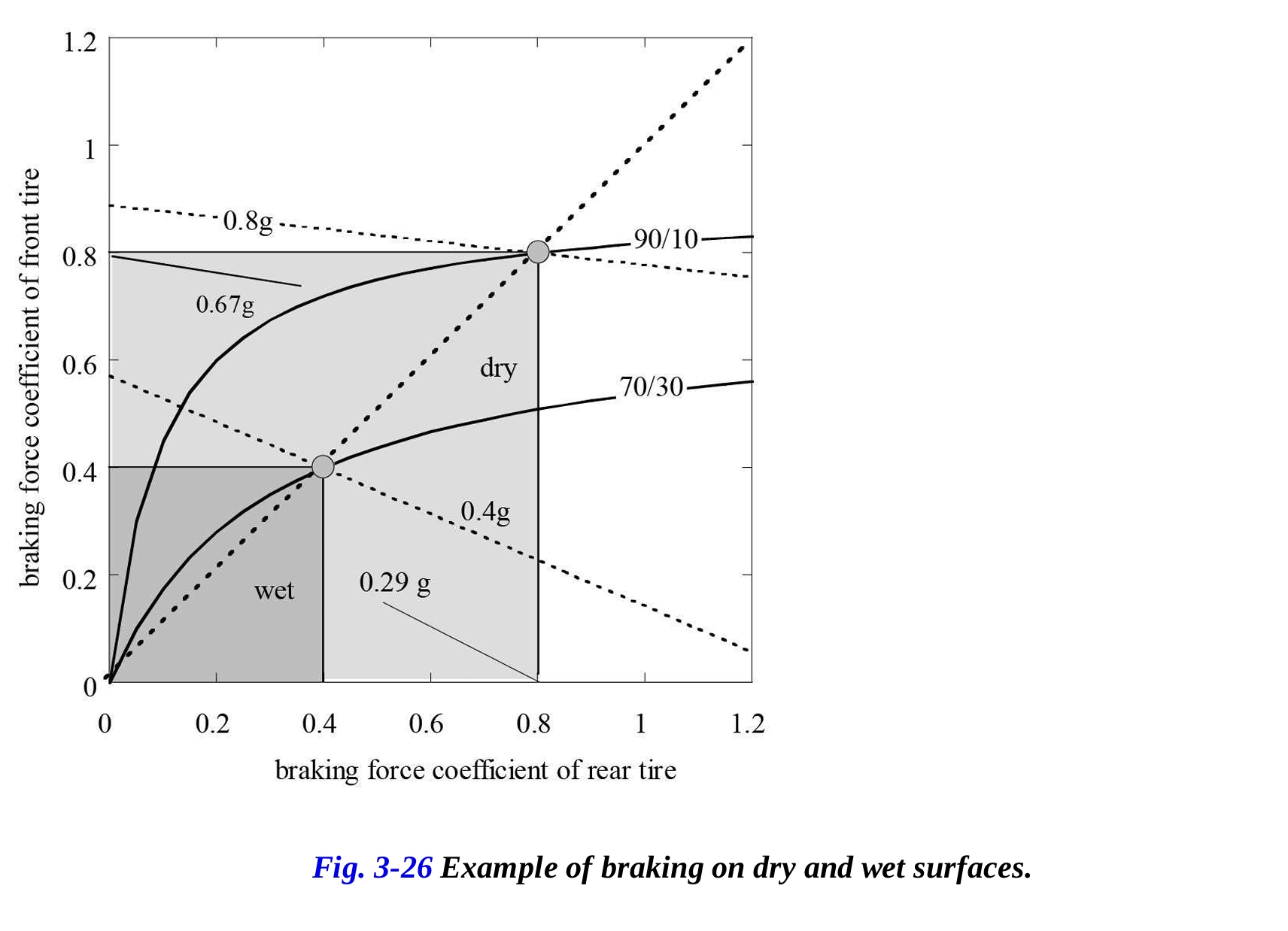
この例から、望ましい減速を変える際には、最適なブレーキングには異なるブレーキ分布が必要であることが分かります。実際、μf = μrに対応する45°の直線は、異なる減速を考慮した際に異なるブレーキ分布の曲線と交差します。これは、いくつかのオートバイに装備されている自動ブレーキ分配装置が、道路の状況に応じて分布を調整する必要があることを意味します。

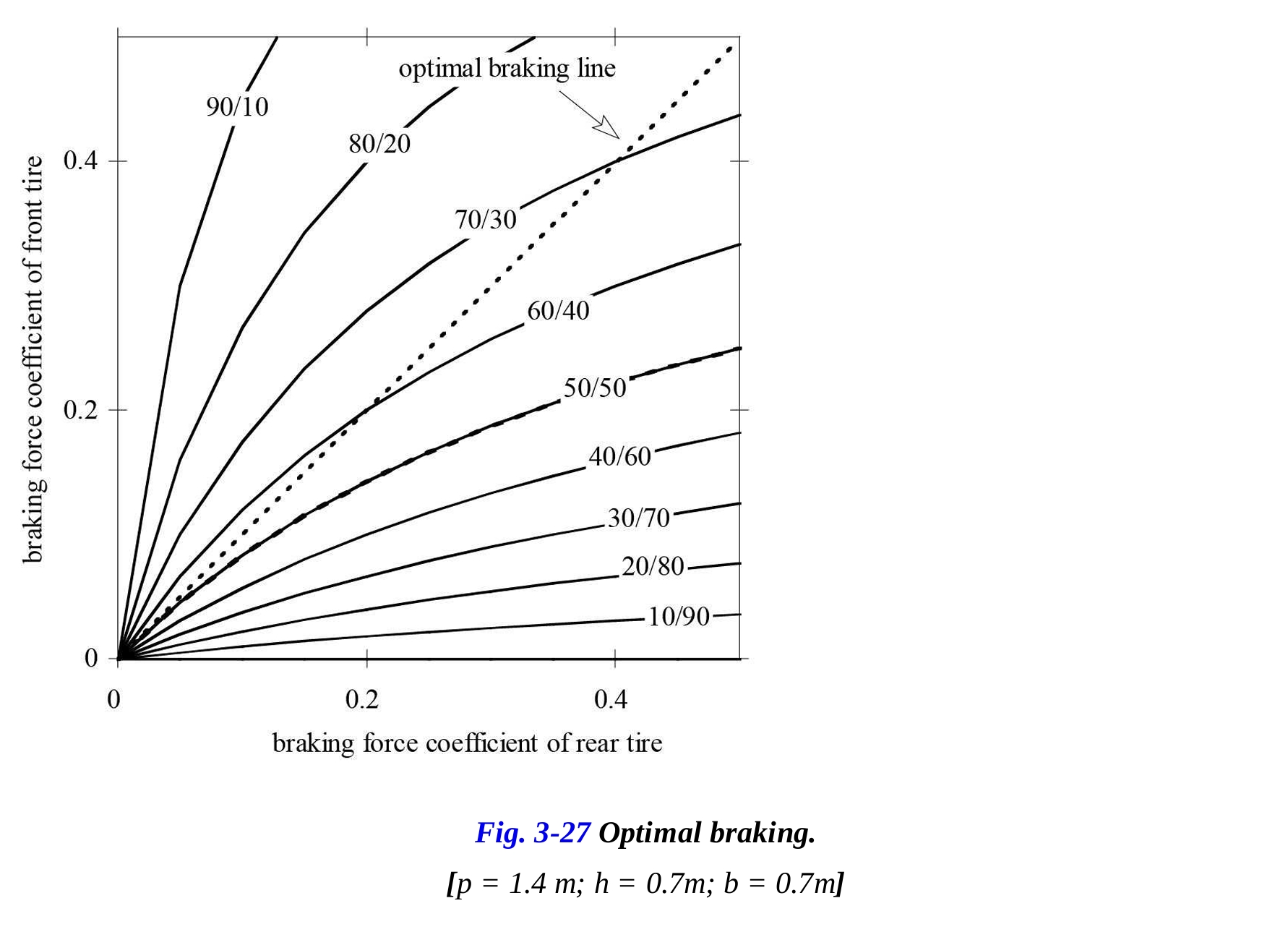
さらに、この例では、後輪のブレーキ力を前輪よりも大きくするのは良い考えではないことも指摘されています。図3-27は、最適なブレーキ分布（点線）が原点で50%対50%の分布曲線に接線でありますが、後輪により大きな力を与える分布曲線とは交差しないことを示しています。

これは、前輪と後輪の静的荷重が異なるオートバイでも同様に有効です。例えば、前輪に45%、後輪に55%の荷重が分配されている場合でも、最適なブレーキング線は常に前輪と後輪の静的荷重が同じ分布を持つブレーキ分布曲線に接線であることが示されます。

4　定常旋回

定常旋回中、オートバイはニュートラル、アンダーステア、またはオーバーステアの挙動を示すことがあります。バランスを維持するために、ライダーはハンドルバーにトルクを加えます。このトルクはゼロ、ポジティブ（ハンドルバーの回転方向と同じ方向）、またはネガティブ（ハンドルバーの回転方向とは反対の方向）であることがあります。これらの特性は、オートバイのハンドリングの感覚を定義する上で重要です。

4.1　定常旋回中のオートバイのロール

4.1.1　理想的なロール角

定常旋回中のオートバイは、以下の2つのモーメントによって影響を受けます。一つは遠心力によって生成される回復モーメントであり、これはオートバイを垂直な位置に戻そうとする力です。もう一つは重力によって生成される傾斜モーメントであり、これはオートバイの傾斜やロール角を増加させようとする力です（図4-1参照）。

次の単純化仮説を導入します。

• バイクは一定の速度で一定半径の円を走行しています（定常状態条件）
• ジャイロ効果は無視できるものとします

タイヤの断面厚さをゼロと考えると、モーメントの平衡から、前進速度$V$ と曲がり半径$R_c$ （この場合、重心から曲がり軸までの距離）を用いてロール角を導出することができます。

ここで、$\Omega$ はヨー角速度を示し、$V = \Omega R_c$ は車両の前進速度を示します。

平衡状態において、遠心力と重力の合力は、タイヤの接地点を結ぶ線を通過します。この線は、タイヤがゼロの厚さで操舵角が非常に小さい場合、バイクの平面内にあります。実際には、ゼロでない操舵角が与えられると、前輪の接地点は後部フレームのx軸に対して横方向にずれるので、タイヤの接地点を結ぶ線は後部フレームの平面内には含まれません。

4.1.2 有効ロール角

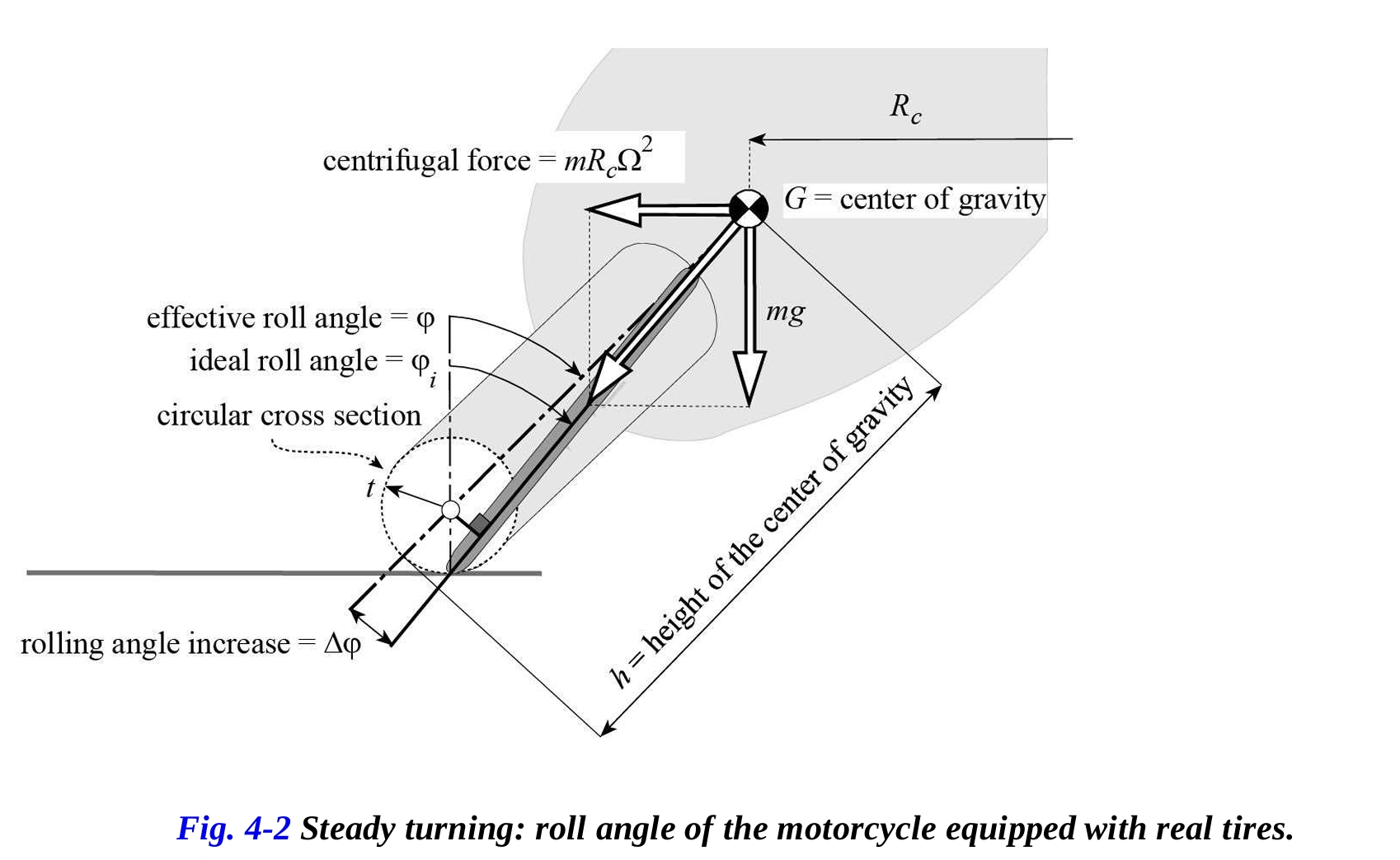
タイヤの厚さが$2 t$ であり、同じヨー角速度$\Omega$ で同じ旋回半径$R_c$ を描くバイクを考えます。タイヤの厚さがゼロでないため、重力と遠心力によって生じるモーメントの平衡に必要なロール角$\phi$ は、理想的なもの$\phi_i$ よりも大きくなります（図4-2）。

ロール角の増加$\Delta \phi$ は次の式で表されます。

有効ロール角は次の通りです。

前述の式は、ロール角と断面半径が増加するにつれて、また重心の高さhが減少するにつれて$\Delta \phi$ が増加することを示しています。したがって、幅広のタイヤを使用すると、断面が小さいタイヤを装着したバイクに比べて、ライダーはより大きなロール角を必要とします。さらに、タイヤの断面が同じである場合、同じ前進速度で同じカーブを描くためには、重心が低いバイクの方が、重心が高いバイクよりも多く傾ける必要があります。

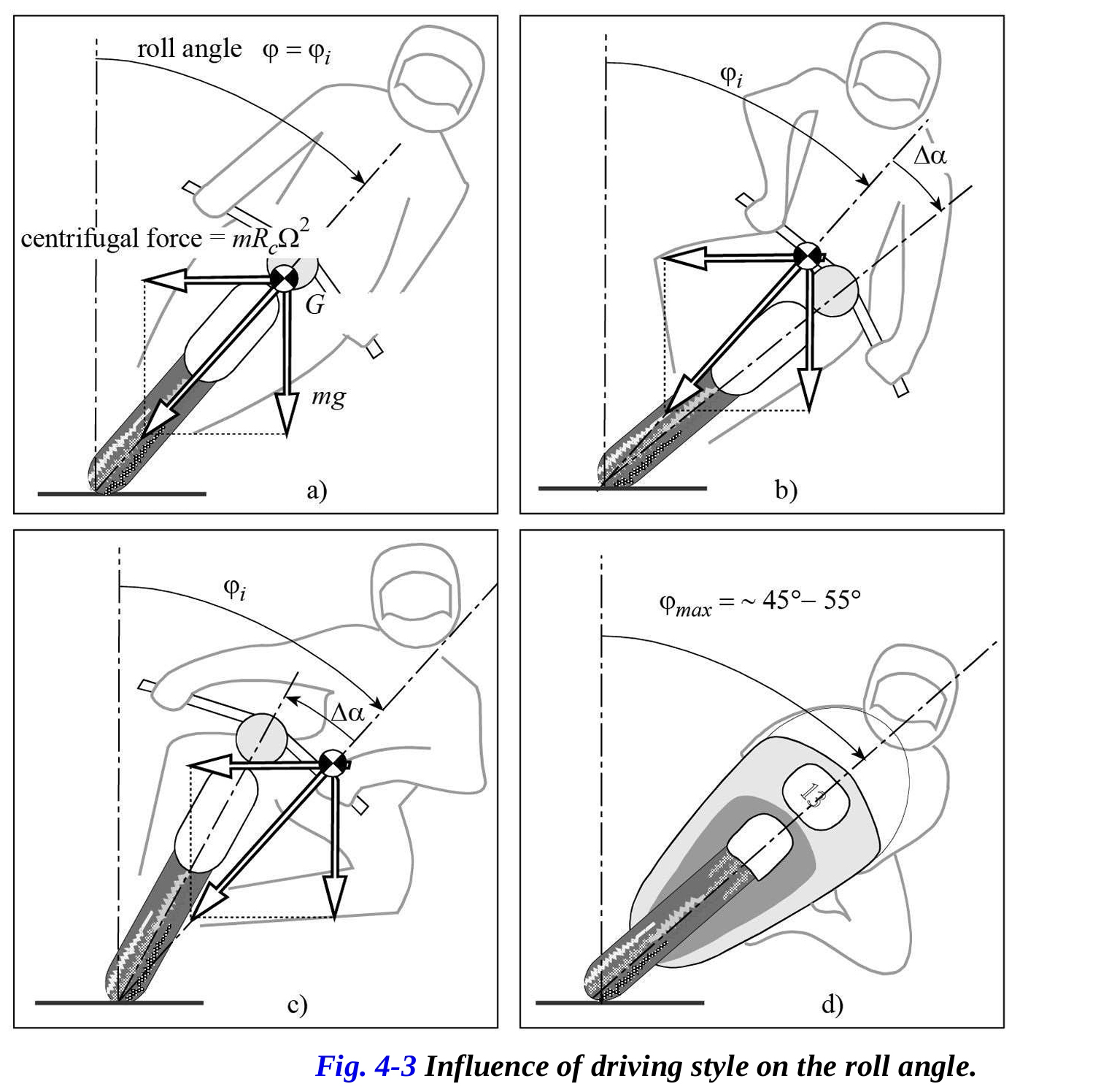
バイクの旋回時のロール角は、ライダーの運転スタイルによって大きく影響を受けます。ライダーがバイクに対して傾くことで、バイクに対する重心の位置が変わります。図4-3は可能な状況を示しています。

ライダーが車体に対して動かずにいる場合（図4-3a）、バイクとライダーのシステムの重心はバイクの平面内に留まります。これは確かにエレガントな方法ですが、最善の方法ではありません。実際、この場合（そしてこの場合のみ）、実際のロール角は以前に計算した理論的なロール角ϕに正確に一致します。

ライダーが旋回の外側に傾く場合（図4-3b）、重心もバイクに対して旋回の外側に移動します。その結果、タイヤが必要以上に傾き、不利な条件下で操作されるため、バイクをさらに傾ける必要があります。このライダーは明らかに初心者です。

ライダーが体幹を旋回の内側に傾け、同時に足を回して膝を地面にほぼ接触させると、バイクの平面のロール角を減少させることができます（図4-3c）。

レースでは、ライダーは旋回の内側に体全体を移動させ、バイクのロール角を減少させるとともに、旋回時の車両の制御をより良くします。バイクとライダーのシステムの重心を内側に移動させるためには、足を動かすだけでなく、サドル内で体を動かします（図4-3d）。体を内側に移動させ、特に足を回転させることにより、旋回の進入と通過を容易にする空力的なヨーイングモーメントが生じます。